
初心者向け:データ分析④
1. はじめに
こんにちは、大学院生のYukiです。
今回はこちらからの引き続きの記事になります。
今までと同様に基本的に図の読み方などは示しますが、ターミナル上に表示される値はこちらに書きませんので、具体的な数値はSpyderやJupyter Notebookなどで自分の手を動かしながら確認をしてみてください。
2. データの前処理をしよう
データ解析にあたりまずはじめに下準備をしましょう。
import numpy as np
from sklearn.model_selection import train_test_split, cross_val_score, KFold, GridSearchCV
from sklearn.neighbors import KNeighborsClassifier
from sklearn import datasets
import matplotlib.pyplot as plt
import warnings
warnings.filterwarnings("ignore")
本日使用予定のライブラリはデータ解析で有名なデータセットのIris(アヤメ)です。こちらはsklearnにあるデータセットなので、ダウンロードは不要です。
float_formatter = "{:.6f}".format
np.set_printoptions(formatter={'float_kind':float_formatter})
iris_data = datasets.load_iris()こちらではiris_dataを作成する前にNumPyの出力オプションを設定しています。具体的には、浮動小数点数の表示方法を、先ほど定義したフォーマッタを使用するように指定しています。これにより、データセット内のNumPy配列の浮動小数点数が6桁の精度で表示されるようになります。
まずはデータの中身を見てみましょう。
print("Feature names: \n", iris_data.feature_names)
print("Target names: \n", iris_data.target_names)
print("Feature data size: \n", iris_data.data.shape)
print("Target data size: \n", iris_data.target.shape)
print("Target values: \n", iris_data.target)'sepal length (cm)':はがく片の長さ、'sepal width (cm)'はがく片の幅、'petal length (cm)'は花弁の長さ、'petal width (cm)'は花弁の幅を表しています。
今回識別するアヤメの種類は'setosa', 'versicolor', 'virginica'の三つです。これらをターゲットバリューとして0,1,2が採番されています。
それではデータセットを分割しましょう。
X_train, X_test, y_train, y_test = train_test_split(iris_data.data, iris_data.target, random_state=142)
print("X_train shape: {}".format(X_train.shape))
print("y_train shape: {}".format(y_train.shape))
print("X_test shape: {}".format(X_test.shape))
print("y_test shape: {}".format(y_test.shape))Xは4つの特徴量を含んだデータ、yはターゲット(アヤメの種類)を含んだデータです。大体75%が訓練(train)用に、25%がテスト用になるよう分割されました。
3. KNN分類を構築しよう
K-近傍法(K-Nearest Neighbors, KNN)は、新しいデータポイントの分類を、訓練データセット内の最も近いデータポイントのラベルに基づいて行います。「近さ」は通常、ユークリッド距離などの距離メトリクスで測定されます。(前回もユークリッド距離は取り扱ったので、わからない方は参照してください。)
例えば、あなたは新しくSNSサービスに新規登録したところです。このサービスには、数百万人の既存利用者のデータが蓄積されています。
まず、あなたは生年月日を入力したり、興味があるトピックなどいくつかの質問に回答します。システムはこの情報を基に、既存の利用者の中からあなたと最も属性や好みが近い人を探します。
そしてその人がよく閲覧している記事をあなたのホーム画面やおすすめ記事として初期表示させます。
新しいデータに対して、既存のデータの中から最も似ているものを探し、その結果に基づいて判断を下す。それがKNN分類法です。
clf_knn = KNeighborsClassifier(n_neighbors=1)
clf_knn.fit(X_train, y_train)上記ではアルゴリズムをオブジェクトとしてインスタンス化し、訓練データという名の過去の記録一覧を与えています。
上記で作成したモデルを使用して、架空のアヤメのデータの予測をしてみましょう。以下に['sepal length (cm)', 'sepal width (cm)', 'petal length (cm)', 'petal width (cm)']を[5, 2.9, 1, 0.2]で割り振ったデータに対して、アヤメの種類の予測をしています。
X_new = np.array([[5, 2.9, 1, 0.2]])
print("X_new.shape: {}".format(X_new.shape))
y_new_pred = clf_knn.predict(X_new)
print("The predicted class is: \n", y_new_pred)結果はいかがでしたか?上記配列だと0のsetosaが予測クラスになっているはずです。数字を変えて予測結果が変わることも確認してみましょう。
作成した訓練データに対し、accuracy_score関数を使って、モデルの精度を計算します。
y_pred = clf_knn.predict(X_test)
accuracy = accuracy_score(y_test, y_pred)
print("Accuracy is: %.4f\n" % accuracy)
結果はいかがだったでしょうか?
データセットが変わっていなければ90%前後という悪くない結果が出ているはずです。
4. CVによるパラメーターチューニング
クロスバリデーション(CV)は、モデルの性能を正確に評価するための方法です。ここでは、KNNモデルの最適な「K」(近くの点をいくつ見るか)を見つけるために使います。
例えば先ほどのテストではKは1で最も近い項目のターゲットのみで判断していました。K値を増やすと次に近いデータポイントのターゲットも閲覧し、最終判断をくだします。
ここではScikit-learnのcross_val_scoreという便利な機能を使い、データを10個の部分に分け、その中の9個で学習し、残りの1個でテストするということを10回繰り返します。このプロセスを異なるK値で何度も繰り返すことで、最も良い結果を出すK値を見つけ、チューニングを行います。
cv_scores = []
cv_scores_std = []
k_range = range(1, 135, 5)
for i in k_range:
clf = KNeighborsClassifier(n_neighbors = i)
scores = cross_val_score(clf, iris_data.data, iris_data.target, scoring='accuracy', cv=KFold(n_splits=10, shuffle=True))
# print(scores)
cv_scores.append(scores.mean())
cv_scores_std.append(scores.std())
plt.figure(figsize=(15,10))
plt.errorbar(k_range, cv_scores, yerr=cv_scores_std, marker='x', label='Accuracy')
plt.ylim([0.1, 1.1])
plt.xlabel('$K$')
plt.ylabel('Accuracy')
plt.legend(loc='best')
plt.show()
こちらでは、K値を1から135まで5刻みで変化させています。各K値に対して、10分割交差検証を行い算出したAccuracyがy軸にプロットされています。縦に伸びている線はエラーバーです。
グラフから、K値が10前後で最も高い精度が得られていることがわかりますね。数が増えるごとに著しく精度が落ちているようです。これは広い範囲のデータポイントを考慮することで、クラス間の境界がぼやけてしまうためです。
また以下はGridSearchCVを用いて選択したK値が最も精度の高い分類につながるかどうかを確認します。GridSearchCVでは複数の異なるデータ分割(クロスバリデーション)を使用しています。上記のマニュアル計算とは異なり、より細かいKの値の組み合わせを試すことができるため、マニュアル計算では見逃していた最適なKの値を発見する可能性があります。
parameter_grid = {'n_neighbors': range(1, 135, 5)}
knn_clf = KNeighborsClassifier()
gs_knn = GridSearchCV(knn_clf, parameter_grid, scoring='accuracy', cv=KFold(n_splits=10, shuffle=True))
gs_knn.fit(iris_data.data, iris_data.target)
print('Best K value: ', gs_knn.best_params_['n_neighbors'])
print('The accuracy: %.4f\n' % gs_knn.best_score_)
cv_scores_means = gs_knn.cv_results_['mean_test_score']
cv_scores_stds = gs_knn.cv_results_['std_test_score']
plt.figure(figsize=(15,10))
plt.errorbar(k_range, cv_scores_means, yerr=cv_scores_stds, marker='o', label='gs_knn Accuracy')
plt.errorbar(k_range, cv_scores, yerr=cv_scores_std, marker='x', label='manual Accuracy')
plt.ylim([0.1, 1.1])
plt.xlabel('$K$')
plt.ylabel('Accuracy')
plt.legend(loc='best')
plt.show()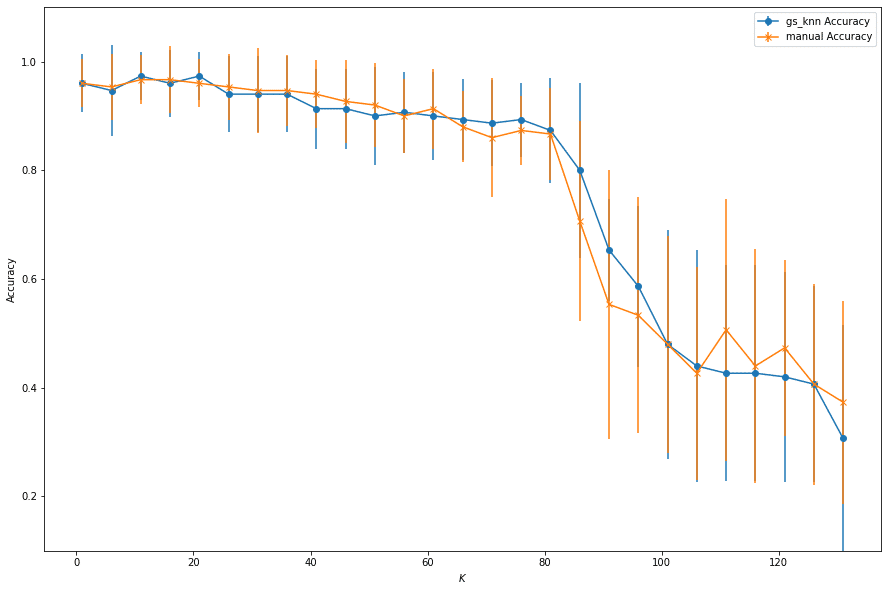
ターミナルに最も高いK値と精度の値が確認できたでしょうか?図では青い線がGridSearchCVを使用して得られた結果を示し、オレンジの線が手動で計算された結果を表しています。
若干精度は上がっていますが、違いはあまり感じられませんね。しかし、GridSearchCVは複数のデータセットで評価し平均を取る手法のため、より信頼性が高く、実際のモデル性能をより正確に反映していると考えられています。
今回のKNN分類を使用したデータ分析はここまでです。
5. おまけのナイーブベイズ法
少し短かったのでここからは少し応用で、ナイーブベイズ法を取り扱います。脱初心者向けの内容になるかもしれませんが、有名なのでこんなのがあるのか、、と名前と特徴だけ知っておくと良いです。
ナイーブベイズ法は、ベイズの定理を使用して、与えられた特徴量に基づいてデータポイントがどのクラスに属する確率が最も高いかを計算する分類アルゴリズムです。この手法が「ナイーブ」と呼ばれる理由は、全ての特徴量が互いに独立であると仮定するためです。(実際にはこの仮定が成り立たないことが多いようですが、、)
ナイーブベイズ法は主に以下の2種類が使用されます。
ガウシアンナイーブベイズ:連続値の特徴量に適用
多項分布ナイーブベイズ:離散値の特徴量に適用
ではまず初めに、連続値としてガウシアンナイーブベイズを取り扱いましょう。
X, y = make_classification(n_samples=100, n_features=2, n_informative=2, n_redundant=0, n_classes=3, n_clusters_per_class=1, weights=None, flip_y=0.01, class_sep=0.5, hypercube=True, shift=0.0, scale=1.0, shuffle=True, random_state=42)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=.2, random_state=42)
colors = ['green', 'yellow', 'purple']
for i, color in enumerate(colors):
plt.scatter(X_train[y_train == i, 0], X_train[y_train == i, 1], c=color)
plt.scatter(X_test[:, 0], X_test[:,1], c='red', marker='x', label='Testing Data')
plt.legend(loc='best')
plt.show()
clf = GaussianNB()
clf.fit(X_train, y_train)
y_pred = clf.predict(X_test)
accuracy = accuracy_score(y_pred, y_test)
print('Testing accuracy is: %.4f\n' % accuracy)
print('Estimated probability of classess: \n', clf.class_prior_)
print('Estimated mean for each Gaussian distribution: \n', clf.theta_)
print('Estimated variance for each Gaussian distribution: \n', clf.sigma_)
clf = GaussianNB()
scores = cross_val_score(clf, X, y, scoring='accuracy', cv=10)
print('Gaussian Naive Bayes accuracy range: [%.4f, %.4f]; mean: %.4f; std: %.4f\n' % (scores.min(), scores.max(), scores.mean(), scores.std()))
こちらでは、まずmake_classification関数を使用して、2次元の合成データセットを生成し、訓練セットとテストセットに分割しています。
次のブロックでは訓練データを3つのクラスに分けてバラバラの色で散布図にプロットし、テストデータも同様に赤いバッテンでプロットしています。

うまくガウシアン向きの連続値になってくれたようです。ではガウシアンナイーブベイズ法を適応させてみましょう。
次のブロックではGaussianNB()でモデルを初期化し、fit()メソッドで訓練データを使って学習させ、予測を行い、正確度(accuracy)を計算しています。(こちらは即席データサンプルなので結果まで記載してしまします。)
Testing accuracy is: 0.7500
Estimated probability of classess:
[0.325000 0.337500 0.337500]
Estimated mean for each Gaussian distribution:
[[0.540523 -0.489185]
[0.542401 0.530535]
[-0.454125 -0.409559]]
Estimated variance for each Gaussian distribution:
[[0.282652 0.184783]
[0.864641 0.747669]
[0.093264 0.368578]]
結果によれば、このモデルは75%の正確さを持っているようです。
その結果も3つのクラスがほぼ均等に分布し33%の確率で出現しています。Estimated mean for each Gaussian distributionでは各クラスの2つの特徴量(xとy)に対する平均値を示しています。Estimated variance for each Gaussian distributionではどれだけ広い範囲に分布しているかを示しています。
Gaussian Naive Bayes accuracy range: [0.6000, 0.9000]; mean: 0.7700; std: 0.0900
モデル性能ですが、10分割交差検証を行い算出した精度は最低が60%、最高が90%だそうです。(チューニングでもやりましたね。)
10回のクロスバリデーションの平均正確度は77%ほどで程よい精度です。正クロスバリデーションによる確度のばらつきは9%ほどなので、正確さの標準偏差の範囲は約68%~86%であることを示しています。
つまり、10分割交差検証の結果、このモデルはデータの分割方法によって性能が大きく変動することは少ないと解釈できます。
(上記は結果の読み取り方の解説なので、実際にはmake_classificationのrandom_stateで大きく値が変わります。)
簡単なガウシアンナイーブベイズ法のやり方とパラメーターチューニングの方法でした。
では以下で実際のあやめのデータセットを使用しながら、今度は多項分布ナイーブベイズを行ってみましょう。
X = iris_data['data']
y = iris_data['target']
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=42)
clf_mnb = MultinomialNB()
clf_mnb.fit(X_train, y_train)
y_pred = clf_mnb.predict(X_test)
accuracy = accuracy_score(y_test, y_pred)
print('Accuracy is: %.4f\n' % accuracy)
print('Estimated probability of classess: \n', np.e**clf_mnb.class_log_prior_)
print('Estimated class-conditional probabilities for each feature: \n', np.e**clf_mnb.feature_log_prob_)
こちらでは、まず訓練セットとテストセットに分割したのち、次ブロックで多項分布ナイーブベイズのインスタンスを作成し適応させています。
その予測と正確さは以下のとおりです。
Accuracy is: 0.9737
Estimated probability of classess:
[0.312500 0.348214 0.339286]
Estimated class-conditional probabilities for each feature:
[[0.490519 0.337423 0.145287 0.026771]
[0.413855 0.194365 0.297918 0.093862]
[0.382610 0.175127 0.324030 0.118233]]
非常に高い正確性です。あやめのデータセット出現確率(Estimated probability of classes)はほぼ均等です。特徴量ごとの条件付き確率は0番目のsetosaだと'sepal length (cm)'のがく片の長さと'sepal width (cm)'のがく片の幅が49%と33%で非常に特徴的だそうです。
また以下ではラプラス補正(alpha=0)を設定しています。デフォルトは1.0のラプラス補正は、ナイーブベイズ分類器で使用される技術で、ゼロ確率問題を解決するために用いられます。
clf_mnb = MultinomialNB(alpha=0)
clf_mnb.fit(X_train, y_train)
print('Estimated probability of classess: \n', np.e**clf_mnb.class_log_prior_)
print('Estimated class-conditional probabilities for each feature: \n', np.e**clf_mnb.feature_log_prob_)
例えば訓練データでは、setosa種の「花弁(petal width (cm))」が常に0.1cmから0.4cmの範囲内だったとします。しかしテストデータに、setosa種の「花弁の幅」が0.5cmのサンプルが現れた場合、alpha=0でラプラス補正がかかってないとモデルはこのサンプルをsetosa種と分類する可能性を完全に排除してしまいます。
そのような結果に柔軟性に富んだ予測ができるようにするのがこの補正です。
ラプラス補正を0にするのは、例えば大規模で十分にサンプルデータが取れているデータセットの処理や、非常に高精度の予測が求められている時だけなので、
基本的には150しかデータのないあやめの場合は設定する必要はありません。
6. 最後に
今回はあやめのデータセットを使いKNN分類法とナイーブベイズ法を解説を行いました。
解説記事は時間を見つけて書いているので今のところ次回は未定ですが、テキスト処理(センチメント分析)や画像解析など行えたら良いな、と考えています。
最後まで読んでいただき、ありがとうございました。
Yuki
