
パスカルの三角形とフィボナッチ数列との深遠なる関係 ~トポロジカルインデックスを介して~
みなさんはパスカルの三角形、あるいはフィボナッチ数列をご存じですか?
高校数学で習ったという人も多いでしょう。
実はこの二つの間には、色々と面白い関係が成り立つことが知られているのです。今日は、その中からグラフ理論にまつわる話をしたいと思います。
まずは、パスカルの三角形やフィボナッチ数列とは何か、その説明から始めることにしましょう。
パスカルの三角形とは
パスカルの三角形は、数字を三角形状に配置したものです。両端の数はすべて1になっていて、それ以外は右上と左上にある数の和になっています。

パスカルの三角形の一番上の段を第0段、左端を第0項としましょう。このとき第$${n}$$段、第$${k}$$項の数は、二項係数$${\binom{n}{k}}$$と一致することが知られています(ここで二項係数とは、$${(1+x)^n}$$の展開式における$${x^k}$$の項の係数のことです)。
$$
\binom{n}{k} = \frac{n\cdot(n-1)\cdots(n-k+1)}{k\cdot(k-1)\cdots1}
$$
以下の性質が成り立ちます。
$$
\binom{n}{0}=\binom{n}{n}=1
$$
$$
\binom{n}{k}=\binom{n-1}{k-1}+\binom{n-1}{k}
$$
$$
\binom{n}{k}=\binom{n}{n-k}
$$
また、二項係数$${\binom{n}{k}}$$は$${n}$$個のものから$${k}$$個を選ぶ組み合わせの総数$${{}_nC_k}$$を表していることも押さえておきましょう。
フィボナッチ数列とは
フィボナッチ数列は文字通り、数列の一種です。第0項が0、第1項が1で、それ以降の項は直前の隣接二項の和になっています。
$$
0,1,1,2,3,5,8,13,21,34,55,89,144,\dots
$$
フィボナッチ数列$${\{F_n\}}$$を漸化式で表すと以下の通り。
$$
F_0=0,\;F_1=1,\;F_{n+2}=F_{n+1}+F_n
$$
フィボナッチ数列$${\{F_n\}}$$の一般項は、特性方程式$${x^2=x+1}$$の2根$${\alpha=\frac{1+\sqrt{5}}{2}}$$および$${\beta=\frac{1-\sqrt{5}}{2}}$$を用いて次のように表されます。
$$
F_n=\frac{\alpha^n-\beta^n}{\alpha-\beta}=\frac{1}{\sqrt{5}}\{(\frac{1+\sqrt{5}}{2})^n-(\frac{1-\sqrt{5}}{2})^n\}
$$
フィボナッチ数列に関する公式としては、以下の式が重要なので覚えておいてください。
$$
F_{m+n+1} = F_{m+1}\cdot F_{n+1} + F_m\cdot F_n
$$
両者をつなぐ不思議な関係
ここで再びパスカルの三角形を眺めてみましょう。
角度をずらして見てみると…
不思議なことにフィボナッチ数列が顔を出します。

式にすると以下の通り(ただし、$${\lceil -\rceil}$$は端数切り捨て)。
$$
F_{n+1} = \sum_{k=0}^{\lceil n/2 \rceil} \binom{n-k}{n-2k} = \sum_{k=0}^{\lceil n/2 \rceil} \binom{n-k}{k}
$$
実は、この式には図形的な意味づけが可能なのです。
そのためには経路グラフとそのZインデックスについて説明する必要があります。
経路グラフとそのZインデックス
経路グラフ(path graph)は、いくつかの頂点を横一列に並べ、隣接する頂点同士を辺でつなげた形をしています。ちょうどn個の頂点(とn-1本の辺)からなる経路グラフを$${P_n}$$で表すことにしましょう。
経路グラフ$${P_n}$$に対して、互いに隣り合わない(頂点を共有しない)辺を何本か選ぶ組み合わせの総数を、$${P_n}$$に対するZインデックスと呼び、$${Z_{P_n}}$$で表します。
「何本か選ぶ」というのは、0本選ぶ(すなわち、何も選ばない)ことも含まれます。また、経路グラフ$${P_n}$$にはちょうどn-1本の辺があるので、互いに隣り合わないように取れる辺の数は最大で$${\lceil n/2\rceil}$$本です(ただし、$${\lceil -\rceil}$$は端数切り捨て)。
例えば、5個の頂点からなる経路グラフ$${P_5}$$の場合、Zインデックスは下図の通り$${Z_{P_5}=1+4+3=8}$$となります。

経路グラフ$${P_n}$$とそのZインデックス$${Z_{P_n}}$$の値を表にしてみましょう。

驚くことに、パスカルの三角形とフィボナッチ数列が顔を出します。
何故、こうなるのでしょうか?
Zインデックスによる図形的な意味づけ
まず、経路グラフ$${P_{n+2}}$$のZインデックス$${Z_{P_{n+2}}}$$について考えてみましょう。頂点がn+2個、辺がn+1本あります。
Zインデックスとは、互いに隣り合わない辺を何本か選ぶ組み合わせの総数でした。そこで、一番左端の辺を選ぶかどうかで場合分けしてみます。
左端を選ばないとき ・・・ 左端を除いた$${P_{n+1}}$$から辺を何本か選ぶ総数$${Z_{P_{n+1}}}$$と一致する
左端を選ぶとき ・・・ その隣の辺を選ぶことができないので、結局左の2本の辺を除いた$${P_n}$$から辺を何本か選ぶ総数$${Z_{P_n}}$$と一致する
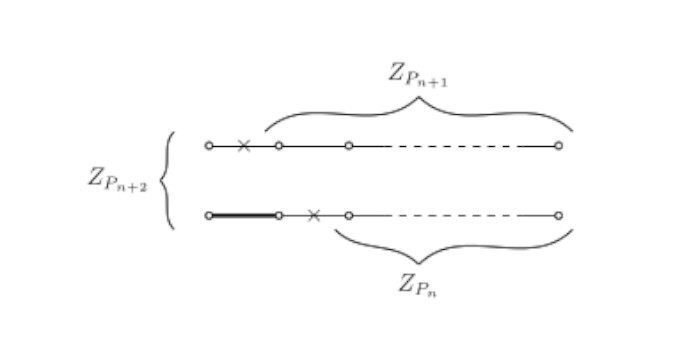
以上より、$${Z_{P_{n+2}}=Z_{P_{n+1}}+Z_{P_n}}$$が成り立ちます。また、$${P_0,\;P_1}$$については共にZインデックスが1なので、数列$${Z_{P_0},Z_{P_1},Z_{P_2},\dots}$$はフィボナッチ数列の第1項以降と一致することが分かります。
$$
Z_{P_n}=F_{n+1}
$$
次に、経路グラフ$${P_n}$$について、互いに隣り合わない辺をちょうど$${k}$$本選ぶ組み合わせの総数がいくつになるか考えてみましょう。
少し考えてみれば分かりますが、経路グラフ$${P_{n-k}}$$のn-k個の頂点の中からk個選んで、そこに辺を挿入すればそれらが隣り合うことはないわけです。したがって、その総数は$${\binom{n-k}{k}}$$です。

Zインデックスはそれらを$${k=0}$$から$${\lceil n/2\rceil}$$まで足し合わせたものなので、
$$
Z_{P_n}=\sum_{k=0}^{\lceil n/2 \rceil} \binom{n-k}{k}
$$
となり、お目当ての式が完成します。
$$
F_{n+1}=\sum_{k=0}^{\lceil n/2 \rceil} \binom{n-k}{k}
$$
このように、この式の図形的な意味づけが可能なことが分かりました。すなわち、経路グラフのZインデックスを違った視点から求めたものだったわけです。
さらに…
フィボナッチ数列を説明したときに紹介したこの公式、
$$
F_{m+n+1} = F_{m+1}\cdot F_{n+1} + F_m\cdot F_n
$$
これもZインデックスで説明できるのです。
$$
Z_{P_{m+n}} = Z_{P_m}\cdot Z_{P_n} + Z_{P_{m-1}}\cdot Z_{P_{n-1}}
$$

発見したのは日本の化学者だった
以上のような事実を世に広めたのは、日本の化学者(数学者ではなく!)細矢治夫でした(※敬称略)。ガソリンのオクタン価に関わる化学の問題を数学的に解明しようというのがもともとの動機だったそうです。
彼は最初、Zインデックスのことを表すのにトポロジカルインデックスという造語を考えていたそうですが、現在ではZインデックスに限らず類似のインデックスを含めた総称として使われています。なお海外では、ZインデックスのことをHosoya indexとも呼びます。
蛇足ですが、グラフ理論においては互いに隣り合わない辺の組み合わせのことをマッチングと呼びます。何故そう呼ぶかというと、例えば、「集団お見合いの場でカップルをできるだけたくさん作るにはどう組み合わせればよいか」といった問題を念頭に置いているからです。
グラフ理論のように、数学の中で亜流の分野においては用語にばらつきがあるので、独自で調べるときには注意が必要です。
まとめ
パスカルの三角形とフィボナッチ数列とは、Zインデックスによって図形的につながっています。
これを発見したのが、数学者ではなく化学者というのも面白いですね。
最後に、参考にした書籍を紹介して終わります。
最後まで記事を読んでいただきありがとうございました!
