
【空間論5】プラトン立体
宇宙創成について語るプラトンの対話篇『ティマイオス』。「宇宙の身体」篇では、宇宙を構成する「火」「空気」「水」「土」という四元素を「正多面体」に結びつける独特な空間理論が示されます。
プラトンが主催する学園アカデメイアの入口には「幾何学を知らざるものは入るを許さず」と大書されていたといわれるように、プラトンは幾何学を重視し、幾何学を用いて宇宙を説明しました。
これに因んで、正多面体は「プラトン立体」と呼ばれます。
プラトン立体(Platonic solids)
四元素説とは、この宇宙が「火」「空気」「水」「土」の4つの要素から構成されるという概念で、エトナ山火山に投身自殺した自然哲学者エンペドクレスが最初に提唱したといわれます。
「火」「空気」「水」「土」を4つのリゾーマタ(根の物質)として、リゾーマタが互いに混合することで事象の生成が起こり、分離することで事象の消滅が起こるというものです。
プラトンは『ティマイオス』において、 当時の常識といえる四元素説を継承し、質料として「火」「空気」「水」「土」の四元素があると説明します。しかし、プラトンは、エンペドクレスと異なり、これらの元素は分解できるばかりか、元素同士も転化すると動的に捉え、これらを正多面体に結びつけて説明します。
火 正4面体
空気 正8面体
水 正20面体
土 正6面体(立方体)
正多面体とは、① 各面がすべて同じ正多角形で、② 各頂点で出会う正多角形の個数が等しい、という条件を満たす立体です。正多面体は4、6、8、12、20の5種類しかなく、このことはプラトンより前の時代に発見されていました。プラトンは、このうち4種類の立体を四元素と結びつけて宇宙の構造を説明しました。

「土」には、最も座りが良いという理由で、正方形からなる「正6面体」を与えました。
他の三元素には、三角形からなる3つの正多面体を与えています。最も軽い「火」は、最も小さくて角張っている「正4面体」、最も重い「水」は球に近い「正20面体」、その中間にある「空気」を「正8面体」としました。
正多面体のうち唯一、正5角形からなる正12面体は、神が宇宙を描写するのに用いたという理由で元素の対応から外されています。
そして、「水」は蒸発すると「空気」になり、「火」は「空気」より軽いといったように、各元素はそれぞれの重さに応じて「運動」すると考えます。
また、正8面体(空気)を2つに分解すると正4面体(火)になるように、一つの正多面体を解体して別の正多面体を作ることで、元素から元素への「転化」が起こると解釈しました。
さらに、これら四元素の相互作用と相互変換によって、「熱い」「冷たい」「重い」「軽い」、あるいは「快」「苦」などが生じるといいます。
こうした運動や転化の考え方は、その後アリストテレスに引き継がれていきます。
なお、四元素と正多面体とを最初に関係づけたのは、プラトンに先立つピタゴラス学派です。ピタゴラス学派の根本思想は均整と調和の理念であり、これが宇宙全体を支配していると考えていました。
プラトンは、このようなギリシアで継承されてきた知識を整合し、『ティマイオス』で言及したことから、これ以後、正多面体は「プラトン立体(Platonic solids)」と呼ばれるようになりました。
双対(そうつい ; Duality)
ところで、プラトン立体には、「双対(そうつい)」と呼ばれる2つの立体間のユニークな関係性がみられます。
例えば、立方体と正8面体。
立方体を構成している6つの正方形の重心を頂点として結ぶと、正8面体になります。その正8面体を構成している8つの正三角形の重心を頂点として結ぶと、初めと同じ立方体になります。このように、二つの正多面体がお互い接しながら交互に出現する関係性を「双対」と呼びます。
「双対」は、立方体と正8面体の組み合わせの他に、正12面体と正20面体、正4面体と正4面体(これは自己双対という)にみられる関係です。
プラトンは、この「双対」に触れていませんが、いずれにせよ正多面体は幾何学的に互いが関係しあうユニークな性格を持ち合わせる立体であり、元素の実体と考えたことは納得がいきます。

ダ・ヴィンチが描くプラトン立体
プラトン立体は、その後、多くの人々に引用されています。
複式簿記を生み出したことでいられる数学者ルカ・パチョーリは、幾何学的立体図形に関する研究を行い1509年、『神聖比例論』を出版しました。これは、ミラノ公イル・モーロの宮廷に招かれた感謝の印として書き起こされたものです。
この著作の第一部「神聖比例の梗概」でパチョーリは、プラトン立体の作図とその意味について、古今の哲学者や神学者からのおびただしい引用を用いて説明しています。そこに記された60点にも及ぶ多面体挿絵は大変正確に描かれており、パチョーリ自身が記すところによれば、レオナルド・ダ・ヴィンチが作図したとのことです。パチョーリとレオナルド・ダ・ヴィンチはミラノ公の宮廷で知り合い、親密に交流していたといいます。

ケプラーによる惑星軌道計算
ケプラーの法則で有名な天文学者ケプラーは、プラトンやピタゴラス贔屓で知られています。ケプラーは、宇宙が数学的な調和、幾何学的秩序に従っていると確信していました。彼の初期の著作『宇宙の神秘』では、太陽系の惑星の軌道を、無数にある立体の中で明確な法則性をもっているプラトン立体で幾何学的に説明しています。
当時惑星は、水星、金星、地球、火星、木星、土星の6つしか発見されておらず、その6惑星が作る5つの間隔を、5つのプラトン立体と関連づけて説明しました。
ケプラーは、最も内側の水星軌道が載る球に正8面体が外接し、その8面体が金星軌道の載る球に内接すると考えます。同様に、金星と地球、地球と火星、火星と木星、木星と土星が、それぞれ正20面体、正12面体、正4面体、正6面体の外接・内接関係に対応すると考えました。
この軌道計算は、当時の観測結果とほぼ一致していました。しかし残念ながら、その後発見された天王星やそれより外部の惑星には当てはまらず、また、火星の観測データをもとにケプラー自身が発見した惑星の楕円軌道(ケプラー第一法則)とも矛盾していました。ただ、ケプラーは終生、プラトンの立体説を重視していたといいます。
なお、ケプラーは数多くの発見をしましたが、「星型正多面体」を発見したことでも知られています。これはプラトン立体が凸型の正多面体であるのに対して、凹を含む正多面体で、「ケプラー・ポアンソ立体」と呼ばれることもあります。
1619年にケプラーは正12面体と正20面体の辺を星型化することにより、2つの星形正多面体(小星型12面体と大星型12面体)を発見しました。その後ポアンソが、大12面体と大20面体を発見し、1811年にルイ・コーシーによって星型正多面体はこの4種類しかないことが証明されています。
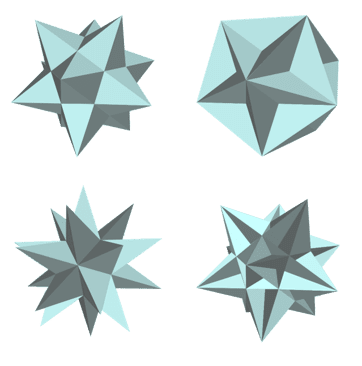
書きおえて
最後まで読んでいただき、ありがとうございました。
(丸田一如)
〈参考〉
プラトン『ティマイオス/クリティアス』岸見一郎訳、白澤社
『 プラトン全集12 ティマイオス クリティアス』、 種山恭子訳、 岩波書店
