位相群の性質 -位相、分離公理、距離付け-

2024年6月18日 18:56

コラム

まさかの続きを書きました(ご苦労様！)。以前に投稿した記事は、自分としてはとりあえず書いてとりあえず放り投げておこう、くらいにしか考えていなかったのですが、友人が反応を示してくれました(ありがたいですね)。と同時にとても読めたものではなかったと反省しました。

そこで、コラムとして平易な話題を最初に書いて少しでも読めるものを、と思った次第です。

フェルマーの小定理

群論に絡めて、次の定理を紹介したいと思います。

定理(フェルマーの小定理)
$${p}$$が素数で、$${a}$$が$${p}$$の倍数ではない正の整数のとき

$$
a^p\equiv a \ \ (\rm{mod} \ \ p)
$$

…なんのことだか。($${{\rm{mod}} \ p}$$というのは両辺の$${p}$$で割ったあまりが同じ、という理解で大丈夫です。) 計算例が面白く感じているので、以下証明は読み飛ばしていただいて問題ありません(区切り線の間)。

以前の記事で剰余群というものを導入しました。いま、整数の集合 $${\mathbb{Z}=\{ \dots, -1, 0, 1,\dots \}}$$として、その部分集合 $${n\mathbb{Z}=\{\dots, -n, 0, n\}}$$を考えます。$${\mathbb{Z}}$$は普通の足し算に関して群で、$${n\mathbb{Z}}$$ は(正規)部分群となります。

したがって、剰余群 $${\mathbb{Z}/n\mathbb{Z}}$$を考えることができます。この群の要素は何かを考えます。
二つの整数$${k}$$、$${l}$$が $${\mathbb{Z}/n\mathbb{Z}}$$ の中で同値であるとは、商集合の同値関係の定義から、

$$
k \sim l \iff k-l \in n\mathbb{Z}
$$

つまり、$${k}$$ と $${l}$$ を$${n}$$で割ったときの余りが同じ、ということになります。すなわち、$${\mathbb{Z}/n\mathbb{Z}}$$の中で違う要素は、$${n}$$ で割ったあまりのとりうる数、の分だけあります。それは具体的にいうと、$${0, 1,\dots , n-1}$$ となります。

したがって、$${\mathbb{Z}/n\mathbb{Z}}$$は次のように書くことができます。

$$
\mathbb{Z}/n\mathbb{Z}=(0+n\mathbb{Z})\cup (0+n\mathbb{Z})\cup \dots ((n-1)+n\mathbb{Z})
$$

ここで、$${\bar{k}=k+n\mathbb{Z}}$$と書くことにすると、

$$
\mathbb{Z}/n\mathbb{Z}={\bar{0},\bar{1},\dots, \overline{n-1}}
$$

となります。この剰余集合には、

$$
\bar{k}+\bar{l}=\overline{k+l} ,\ \ \bar{k}\cdot \bar{l}=\overline{kl}
$$

とすることで、和と積の演算を入れることができます。

フェルマーの小定理の意味するところは、$${p}$$が素数で、$${a}$$が$${p}$$の倍数ではない正の整数のとき$${\mathbb{Z}/p\mathbb{Z}}$$において

$$
(\bar{a})^{p-1} = \bar{1}
$$

が成り立つということです。せっかく群論の言葉で書き換えられたので、このまま群論の議論で証明していきます(初等整数論でも証明できますが…)。

まずより一般的に$${a}$$が任意の整数であるとき、

$$
(\bar{a})^{p} = \bar{a}
$$

であることを証明します。ちょっとその前に、準備として次を証明しておきます。任意の整数 $${a, b}$$に対して、

$$
(\bar{a}+\bar{b})^p=(\bar{a})^p+(\bar{b})^p
$$

これは、左辺を２項定理により展開すると、

$$
(\bar{a}+\bar{b})^p=\bar{a}^p+{}_p C_1\bar{a}^{p-1}\bar{b}+{}_p C_1\bar{a}^{p-2}\bar{b} +\dots +{}_p C_{p-1}\bar{a}\bar{b}^{p-1}+\bar{b}^p
$$

ここで、$${{{}_p C_k}=\frac{p!}{k!(p-k)!} \ (k=1,\dots, p-1)}$$で、$${p}$$は素数のため、分母は$${p}$$で割り切れず、分母は$${p}$$で割り切れることとなります。

したがって、

$$
\bar{a}^p+{}_p C_1\bar{a}^{p-1}\bar{b}+{}_p C_1\bar{a}^{p-2}\bar{b} +\dots +{}_p C_{p-1}\bar{a}\bar{b}^{p-1}+\bar{b}^p=\bar{a}^p+\bar{b}^p
$$

となり、証明できました。さて、

$$
(\bar{a})^{p} = \bar{a}
$$

の証明に戻りますが、$${a=0}$$のときはよいので、$${a\neq 0}$$のときを考えます。さらに $${a>0}$$の場合を考えます。このとき上で証明したことを繰り返し使って、

$$
\begin{array}{}
\bar{a}^p=(\overline{1 + (a-1)})^p&=&\bar{1}^p+\overline{a-1}^p \\
&=&\bar{1}^p+(\overline{1 + (a-2)})^p \\
&=&\bar{1}^p+\bar{1}^p+(\overline{a-2})^p \\
&=&\bar{1}^p + \bar{1}^p +\dots \bar{1}^p \\
&=& \bar{a}
\end{array}
$$

$${a<0}$$ のときは、

$$
\bar{a}^p=\overline{(-1)^p(-a)^p}=(-1)^p\overline{(-a)^p}=(-1)^p\overline{-1}
$$

ここで、最後の等号は、$${-a>0}$$であることを用いました。$${p=2}$$とすると、$${\bar{-1}=\bar{1}}$$より、$${(-1)^2\bar{a}=\bar{a}}$$となります。また、$${2}$$以外の素数は奇数なので、$${(-1)^p\overline{-a}=-\overline{(-a)}=\bar{a}}$$となります。つまり、いずれにしても

$$
(\bar{a})^{p} = (-1)^p(\overline{-a}) = \bar{a}
$$

が成り立ちます。なんにせよ、任意の整数$${a}$$に対して、

$$
(\bar{a})^{p} = \bar{a}
$$

がなりたつということです。

次に、$${a}$$が$${p}$$で割り切れない場合、つまり$${\bar{a}\neq\bar{0}}$$のときを考えます。証明したいのは次でした。

$$
(\bar{a})^{p-1} = \bar{1}
$$

少し先が見通しにくくなりそうですが、次のことを証明したいと思います。群 $${\mathbb{Z}/n\mathbb{Z}}$$に対して、掛け算に関する逆元が存在する元の部分集合を $${(\mathbb{Z}/n\mathbb{Z})^{\times}}$$と書くことにすると、

$$
\left(\mathbb{Z}/n\mathbb{Z} \right)^{\times}=\left(\mathbb{Z}/n\mathbb{Z} \right)\backslash \{\bar{0}\} \iff n は素数
$$

これはなぜかというと、任意の整数$${a}$$に対して、

$$
(\bar{a})^{p} = \bar{a}
$$

を証明しましたが、$${\bar{a}\neq\bar{0}}$$の状況においては、$${\left(\mathbb{Z}/p\mathbb{Z} \right)^{\times}=\left(\mathbb{Z}/p\mathbb{Z} \right)\backslash \{\bar{0}\} }$$

であり、$${\bar{a}}$$には積に関する逆元が必ず存在することとなり、

$$
(\bar{a})^{p} = \bar{a}
$$

の両辺に$${\bar{a}^{-1}}$$をかけることで、

$$
(\bar{a})^{p-1} = \bar{1}
$$

が証明できるからです。ということで、

$$
\left(\mathbb{Z}/n\mathbb{Z} \right)^{\times}=\left(\mathbb{Z}/n\mathbb{Z} \right)\backslash \{\bar{0}\} \iff n は素数
$$

の証明に集中します。まず次が証明できます。

$$
(\mathbb{Z}/n\mathbb{Z})^{\times}=\{\bar{a} : gcd(a, n)=1\}
$$

これは次の同値関係から証明できます。

$$
\begin{array}{}
\bar{a}\in (\mathbb{Z}/n\mathbb{Z})^{\times} &\iff& \exist x\in\mathbb{Z} \ s.t \ \overline{ax}=\bar{1} \\
&\iff& \exists x,y\in\mathbb{Z}, \ ax+ny=1 \\
&\iff& gcd(a,n)=1
\end{array}
$$

ここで次の関数を定義します。

定義
正の整数$${n}$$に対し、$${n}$$と互いに素な$${1}$$以上$${n}$$以下の自然数の個数を$${\varphi(n)}$$とかく。これをオイラーの$${\varphi}$$関数という。

したがって、$${(\mathbb{Z}/n\mathbb{Z})^{\times}}$$の元の個数は$${\varphi(n)}$$と一致します。

さらに、$${n}$$が素数の場合は、$${1,\dots, n-1}$$とはすべて互いに素なので、$${\varphi(n)=n-1}$$です。

つまり

$$
\#(\mathbb{Z}/n\mathbb{Z})^{\times}=n-1\iff n は素数
$$

で、$${\bar{0}}$$は掛け算に関する逆元を持たないことから、

$$
(\mathbb{Z}/n\mathbb{Z})^{\times}\subset \mathbb{Z}/n\mathbb{Z}\backslash \{\bar{0}\}
$$

で、両辺の個数は $${n-1}$$ なので(有名な議論ですが包含関係にある有限集合の個数が一致しているときは集合として一致します)、

$$
(\mathbb{Z}/n\mathbb{Z})^{\times}=\mathbb{Z}/n\mathbb{Z}\backslash \{\bar{0}\}
$$

これでようやく、

$$
\left(\mathbb{Z}/n\mathbb{Z} \right)^{\times}=\left(\mathbb{Z}/n\mathbb{Z} \right)\backslash \{\bar{0}\} \iff n は素数
$$

が証明でき、

$$
(\bar{a})^{p-1} = \bar{1}
$$

が証明できました。

ああ、思ったより大変でしたね。

具体例に入りますが例えば次のような問題を簡単に解くことができます。

$${315^{23}}$$を$${23}$$で割ったあまりはなんでしょうか？

答えは、フェルマーの小定理から(23が素数で、315が23で割り切れないため)、

$$
315^{23}\equiv 315\equiv 23\times 13+16\equiv 16
$$

です。

このように、一見不可能に思えることも規則を厳密に理解し定理という形にすることで、実現してしまうのが数学の威力であり魅力であると思います。

これで終わってもいいのですがここからが本題です。

はじめに

今回は位相群の性質(位相、分離公理、距離付け)について述べたいと思います。主に位相側に寄った性質です。
位相群は、位相構造と群構造を同時に持つことに起因して、単位元の周りについて調べれば、全体の様子がわかる、という顕著な性質を持っているのが特徴と考えられます。

位相群の位相

代数演算と、位相構造の間に密接な関係があり、その結果、群構造をもつ $${G}$$ に位相群としての位相を導入するには、全空間にわたる基底を指定する必要はなく、単位元 $${e}$$ の完全近傍系(すべての近傍の族)を指定すれば十分であることがわかります。

部分集合 $${A, B\subset G}$$ に対し、

$$
A\cdot B = \{ x\cdot y\ | x\in A, y\in B\}, \ \ A^{-1} = \{x^{-1} | x \in A \}
$$

などと書く。

定義
集合 $${X}$$ の部分集合の族 $${\mathscr{F}}$$ が次の３条件を満たすとき、 $${\mathscr{F}}$$ は $${X}$$ 上のフィルターという。
(1) $${A, B\in \mathscr{F} \Rightarrow A\cap B \in \mathscr{F}}$$
(2) $${A\in \mathscr{F}, A\subset B \Rightarrow B\in \mathscr{F}}$$
(3) $${\empty \notin \mathscr{F}}$$

位相群の単位元 $${e}$$ の完全近傍系の作るフィルターを $${\mathscr{N}}$$ とする。 $${a}$$ を $${G}$$ の任意の元とするとするとき、写像

$$
x\mapsto a\cdot x; \ \ x\mapsto x\cdot a
$$

は $${G}$$ から $${G}$$ への位相同型写像である。したがって、

$$
a\mathscr{N}=\{aV|V\in \mathscr{N}\}, \mathscr{N}a = \{Va| V\in\mathscr{N}\}
$$

は点 $${a}$$ の完全近傍系になる。このようにして、単位元 $${e}$$ の完全近傍系を知ることにより、ほかの任意の点における完全近傍系を知ることができる。

$${e}$$ の完全近傍系 $${\mathscr{N}}$$ は次の三条件を満たす。
(1) 任意の $${U\in \mathscr{N}}$$ に対して、 $${VV\subset U}$$ を満たす $${V\in\mathscr{N}}$$ が存在する。
証明) 群の乗法演算を $${m: G\times G\rightarrow G}$$ とする。 $${\rm{int}(U)}$$ は $${e}$$ の開近傍であり、$${m}$$の連続性から、$${m^{-1}(\rm{int}(U))}$$ は $${(e, e)}$$ の開近傍なので、 $${V\times V\subset m^{-1}(int(U))\subset m^{-1} (U)}$$ となる $${V\in \mathscr{N}}$$ が存在する。 $${ab\in VV}$$ とすると、 $${(a, b) \in V\times V \subset m^{-1}(U)}$$ より、 $${ab=m((a,b))\in U}$$ したがって、 $${VV\subset U}$$
(2) 任意の $${U\in \mathscr{N}}$$ に対して、 $${U^{-1}\in\mathscr{N}}$$。
証明) 写像 $${x\mapsto x^{-1}}$$ が $${G}$$を$${G}$$ 自身に移す位相同型写像であるから、開写像。したがって、$${e = x^{-1}(e)\in x^{-1}(U^{\circ})=(U^{\circ})^{-1}\subset {U^{-1}}^{\circ} \subset U^{-1}}$$ (後ろから2番目の包合関係は、内部は最大の開集合であることから)。または単に $${e\in (U^{-1})^{\circ}=U^{-1}}$$ なので。
(3) 任意の $${a\in G}$$ 、任意の $${U\in\mathscr{N}}$$ に対して、 $${aUa^{-1}\in \mathscr{N}}$$ 。
証明) $${a\in G}$$を一つ固定したとき、$${x\mapsto ax}$$ 、$${x\mapsto xa^{-1}}$$がいずれも$${G}$$から$${G}$$への位相同型写像、したがって開写像であることから、$${e=aea^{-1}\in aUa^{-1}}$$なので、$${U\in \mathscr{N}}$$。

ここで、フィルター $${\mathscr{N}}$$ について "(1)および(2)" が成り立つことは次の(*)と同値である。
(*) 任意の$${U\in \mathscr{N}}$$に対して、$${VV^{-1}\subset U}$$かつ $${V^{-1}\in \mathscr{N}}$$を満たす$${V\in \mathscr{N}}$$が存在する。
証明) フィルター$${\mathscr{N}}$$について、 (1)と(2)が成り立つと仮定する。任意の$${U\in \mathscr{N}}$$に対して、(1) から$${WW\subset U}$$を満たす$${W\subset \mathscr{N}}$$が存在する。また (2) によって、 $${W^{-1}\in \mathscr{N}}$$であるから、$${V=W\cap W^{-1}}$$とおけば、 $${V\in \mathscr{N}}$$ (フィルターの定義(2))。(2)より $${V^{-1}\in\mathscr{N}}$$かつ$${V^{-1}\subset W}$$となり、したがって $${VV^{-1}\subset WW \subset U}$$。
逆にフィルター$${\mathscr{N}}$$が (*)を満たすとする。このとき任意の $${U\in\mathscr{N}}$$について、 $${e\in U}$$となる。実際、 $${V\in\mathscr{N}}$$ が $${VV^{-1}\subset U}$$ とすれば、 ( $${V}$$は非空であるから)すべての $${x\in V}$$ について、 $${xx^{-1}=e\in U}$$ となるからである。 (*)より $${V\subset VV^{-1}\subset U}$$。したがって、 $${V\subset U^{-1}}$$ であるからフィルターの定義 (2) より $${U^{-1}\in\mathscr{N}}$$ である。 $${V\in \mathscr{N}}$$ が $${VV^{-1}\subset U}$$ を満たすものとし、$${W=V\cap V^{-1}}$$ とおけば、 $${W\in\mathscr{N}}$$ で (フィルターの定義(1)より)かつ $${WW\subset VV^{-1}\subset U}$$ である。

上に定義した $${W=V\cap V^{-1}}$$ は、 $${e}$$ の近傍で、しかも $${W=W^{-1}}$$ が成り立つ。この性質を対称性という。

定理
$${G}$$ を群、 $${\mathscr{N}}$$ を上記の (1)、(2)、(3) を満足する $${G}$$ 上のフィルターとする。このとき$${G}$$を位相群とし、かつ$${\mathscr{N}}$$を単位元$${e}$$の完全近傍系とする$${G}$$の位相が一意に定まる。

証明) 仮に所望の性質を持つ位相が存在するとすれば、各点 $${a\in G}$$ の完全近傍系は、 $${a\mathscr{N}}$$ および $${\mathscr{N}a}$$ からなる集合族と一致する。このようにして、各点の完全近傍系が定まるので、所望の性質を有する $${G}$$ 上の位相はただ一つである。
次の2点を示す必要がある。
(A) フィルター $${a\mathscr{N}}$$ が点 $${a\in G}$$ 上の完全近傍系となる $${G}$$ 上の位相がある。
(位相があること)
(B) この位相について、 $${G}$$ 上の群の演算が連続となる。
( $${G}$$ がこの位相の下で位相群となること)

(A) の証明
これを示すためには各 $${a\in G}$$ について、 $${a\mathscr{N}}$$ が次の４つの条件を満たすことを確認すればよい。
(1) $${U\in \mathscr{N}}$$ に対して、 $${aU\subset P}$$ ならば $${P\in a\mathscr{N}}$$
(2) $${a\mathscr{N}}$$ に属する任意有限個の集合の共通部分は $${a\mathscr{N}}$$ の元である。
(3) 任意の $${U\in \mathscr{N}}$$ について、 $${a\in U}$$
(4) 任意の $${U\in \mathscr{N}}$$ について、

$$
xV\subset aU {\rm{ \ \ for \ \ all \ \ }} x\in aV (したがって、aU\in x\mathscr{N})
$$

を満たす $${V\in\mathscr{N}}$$ が存在する。
(1) と (2) は $${a\mathscr{N}}$$ がフィルターであることを意味している。(それぞれフィルターの定義(2)と(1)から導かれる。) $${\mathscr{N}}$$ の定め方から、(3)も成り立つ( $${e\in U}$$ )。(4) だけ示せば十分である。任意の $${U\in\mathscr{N}}$$ を考えると、完全近傍系の性質(1)より、 $${VV\subset U}$$ を満たす $${V\in\mathscr{N}}$$ が存在する。すると任意の $${x\in aV}$$ に対して、

$$
xV \subset aVV \subset aU
$$

ゆえに、 $${aU\in x\mathscr{N}}$$。

(B) の証明: 演算 $${(a, b)\mapsto ab^{-1}}$$ が連続となることを示す。
$${U}$$ を $${e}$$ の任意の近傍とすれば、 (3)により

$$
V\equiv b^{-1}Ub\in \mathscr{N} \ \ \ \ (1)
$$

この $${V}$$ に対して、(1)、(2) $${\iff}$$ (*) より、 $${WW^{-1}\subset V}$$ なる $${W\in\mathscr{N}}$$ が存在する。いま $${u, v\in W}$$ とすれば、 $${uv^{-1}\in V}$$ であり、したがって、 (1) により、 $${buv^{-1}b^{-1}\in U}$$ 。よって、

$$
u\in W, v\in W \Rightarrow (au)(bv)^{-1}=(ab^{-1})(buv^{-1}b^{-1})\in ab^{-1}U
$$

位相群の分離公理

位相群上の分離公理に関して考えます。一般的に位相空間内の点の分離度合いによっていくつかの種類に分かれます。点(閉集合)と近傍の位置関係により次の $${T_0}$$ ～ $${T_4}$$ などがあります。

$${(T_0)}$$ (Kolmogorovの公理) 相異なる２点の少なくとも一方が他方を含まない近傍を有する。

$${(T_1)}$$ (Fechetの公理) 相異なる２点はそれぞれ他方を含まない近傍を有する。

$${(T_2)}$$ (Hausdorffの公理) 相異なる２点はそれぞれ互いに交わらない近傍を有する。

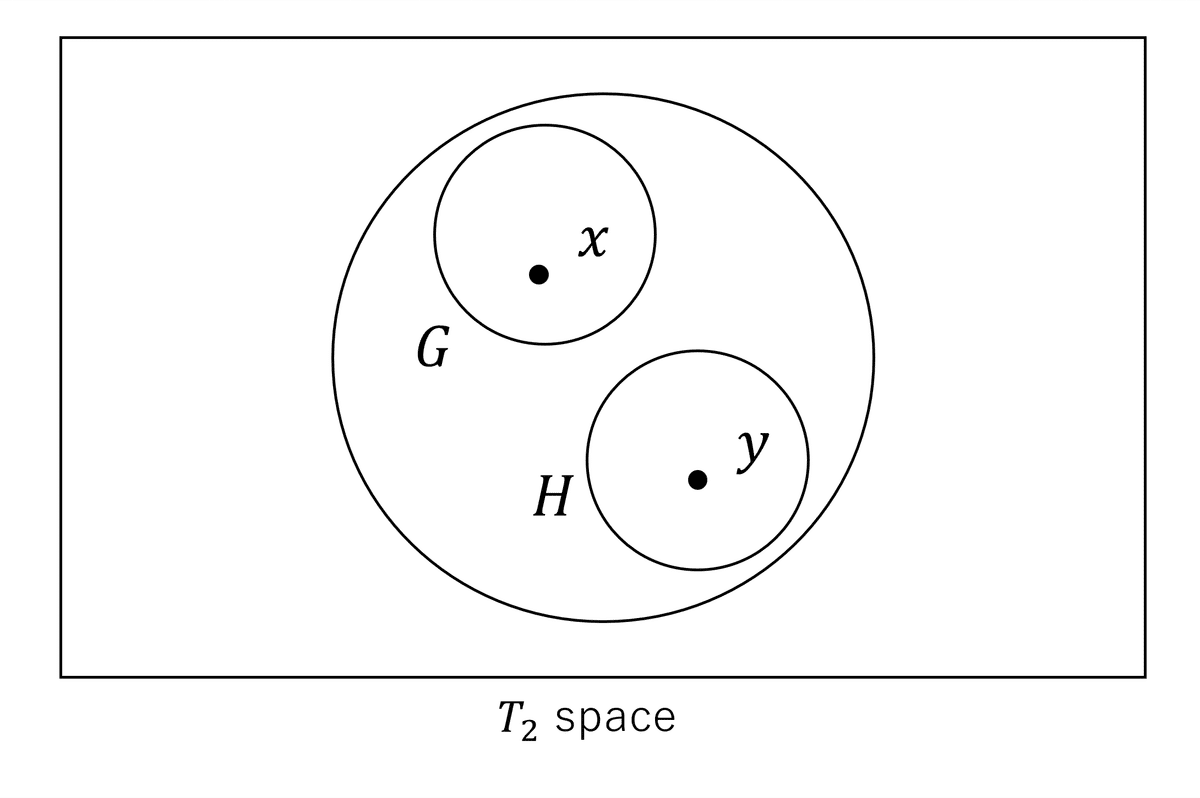
$${(T_3)}$$ (Vietorisの公理) 任意の閉集合 $${F}$$ とこれに含まれない点はそれぞれ交わらない近傍を有し(正則性)、かつ $${T_1}$$。

$${(T_4)}$$ (Tietzeの公理) 交わらない二つの閉集合は互いに交わらない近傍を有し(正規性)かつ$${T_1}$$。

すぐにわかる関係として、

$$
T_4\Rightarrow T_3\Rightarrow T_2 \Rightarrow T_1\Rightarrow T_0
$$

定理(位相群の分離公理)
位相群 $${G}$$ について、 $${T_0, T_1, T_2, T_3}$$ はすべて同値である。

証明) $${T_0\Rightarrow T_2,T_3}$$ を証明すれば十分である。($${T_2}$$を証明するのは、$${T_3}$$であることを証明するときに、$${T_1}$$であることを用いるため。)
$${T_0\Rightarrow T_2}$$: $${a,b\in G}$$, $${a\neq b}$$ とすれば、$${G}$$ が $${T_0}$$ であるから、例えば $${a\in U}$$、$${b\notin U}$$ となる開集合が存在する。このとき互いに交わらない $${a,b}$$ の近傍が存在することを示す。このとき一般性を失うことなく、 $${a=e, b\neq e}$$ および $${e\in U, b\notin U}$$ として証明すれば十分である(一般的には、$${a, b}$$を考えて、$${e, a^{-1}b}$$において証明されていることを利用すればよい。) そこで、 $${VV^{-1}\subset U}$$ を満たす $${e}$$ の近傍 $${V}$$ をとる。 $${e\in V}$$ 、 $${b\in bV}$$ であるから、仮に $${b\cap bV\neq\empty}$$ であるとし、 $${x\in V\cap bV}$$ とすれば、

$$
x\in V \ {\rm{and}} \ x=by \ {\rm{for}} \ {\rm{some}} \ y\in V
$$

したがって、

$$
b=xy^{-1} \in VV^{-1}\subset U
$$

これは $${b\notin U}$$ に矛盾する。
$${T_0\Rightarrow T_3}$$ : $${F\subset G}$$ を閉集合で、 $${e\notin F}$$ とする。このとき $${G\backslash F}$$ は $${e}$$ の近傍であるから、 $${e}$$ の適当な近傍 $${V}$$ をとれば、

$$
VV\subset G\backslash F
$$

とすることができる。これから、前と同様にして、 $${V\cap FV=\empty}$$ となる。また、 $${FV=\cup_{x\in F}xV}$$ であるから、 $${FV}$$ は開集合。そして、 $${e\in V}$$ 、 $${F\subset FV}$$ であるから、正則である。また、 $${G}$$ は $${T_2}$$ でもあるから、 $${T_1}$$ である。したがって、 $${G}$$ は $${T_3}$$ である。

位相群の距離付け

距離から定まる位相があるように(ユークリッド距離から定まる位相)、逆に位相から距離が定まることがあります。それを簡単にいうと距離付け可能であるなどと言ったりします。

距離 $${d}$$ から定められる位相空間を、 $${\mathscr{O}_d}$$ と書くことにする。

定義
与えられた位相空間 $${(S, \mathscr{O})}$$ に対して、 $${\mathscr{O}=\mathscr{O}_d}$$ となるような $${S}$$ 上の距離関数 $${d}$$ が存在するならば、 $${d}$$ はこの位相空間 $${(S, \mathscr{O})}$$ を距離付けるといい、また、 $${(S, \mathscr{O})}$$ は距離付け可能であるという。

位相群の距離付けに関しては、次の定理が知られている。

定理 (距離付け)
$${G}$$ を Hausdorff 位相群とする。このとき、 $${G}$$ が距離付け可能であるための必要充分条件は、単位元 $${e}$$ の加算近傍系が存在することである。さらに、 $${G}$$ が距離付け可能であれば、 $${G}$$ は左不変な、すなわち

$$
\rho(ax, ay) = \rho(x, y) \ {\rm{for}} \ {\rm{all}} \ a, x, y \in G
$$

を満たす $${\rho}$$ によって、距離付け可能である。

証明) 距離付け可能な空間は、加算近傍系が存在する。位相空間 $${X}$$ の距離を $${d}$$ として、

$$
N_{1/n}(a) = \{x\in X : d(x, a)< \epsilon \}
$$

とすると $${N_{1/n}(a)}$$ は点 $${a}$$ の可算基本近傍系となる。実際、任意の $${\epsilon}$$ 対して、アルキメデスの性質(連続性の公理から証明される)からある $${n_0}$$ が存在して、

$$
1< \epsilon n_0
$$

となる。そこで、 $${n\ge n_0}$$ とすれば、$${1/n\le 1/n_0\ < \epsilon}$$ より、

$$
N_{1/n}(a)\subset N_{\epsilon}(a)
$$

となるので、 $${{N_{1/n}(a) }, \ {n\in \mathbb{N}}}$$ は点 $${a}$$ における $${X}$$ の基本近傍系である。さらに、その数は自然数濃度に等しいため、可算である。逆を証明する。 $${N_1,N_2\dots}$$ を $${e}$$ の可算基本近傍系とする。まず $${U}$$ を $${e}$$ の近傍とすれば、 $${V=U\cap U^{-1}}$$ も $${e}$$ の近傍で、 $${V=V^{-1}}$$ である。また、乗法演算の連続性から、基本近傍系の元 $${U}$$ に対して、 $${VVV\subset U}$$ となる近傍系の元がある。 $${V}$$に含まれる基本近傍系の元を $${W}$$ とすれば、 $${(W)^3\subset U}$$ となる。したがって、$${N_k^{\prime} = N_k\cap N_k^{-1}}$$ とし、 $${(N{k+1}^{\prime})^3\subset N_k^{\prime}}$$ となるように選択すれば、新しい $${e}$$ の基本近傍系を、

$${N_k^{\prime}}$$は対称的
$${{N_k^{\prime}}^3 \subset N_k^{\prime}}$$
$${N_k^{\prime}\subset N_k}$$

とすることができる。そこで、はじめから、 $${N_k}$$ が対称的で、しかも $${N_{k+1}^3\subset N_k}$$ を満たすものと仮定してよい。ただし、便宜上、 $${N_0=G}$$ とおく。

関数 $${\sigma: G\times G\rightarrow \mathbb{R}}$$ を次のように定義する。

$$
\sigma: (x,y)\mapsto \frac{1}{2^k} \ \ if \ \ x^{-1}y\in N_k\backslash N_{k+1}, k=0, 1, 2,\dots
$$

とすると、この $${\sigma}$$ は
(1) $${\sigma(x,y)\ge 0}$$
(2) $${\sigma(x,y)=\sigma(y,x)}$$ ( $${N_k}$$ が対称的なため)
(3) $${\sigma(ax,ay)=\sigma(x,y)}$$
を満足する。そこで、 $${\rho: G\times G\rightarrow \mathbb{R}}$$ を

$$
\rho(x,y)=inf_{x_0,\dots,x_n} \{\displaystyle\sum_{i=1}^{n}\sigma(x_{i-1}, x_i): x_0=x,x_1,\dots,x_n=y \}
$$

と定義する。ただし、inf は $${x_0=x, x_1,\dots, x_n=y}$$ となるような、任意有限個の点 $${(x_0,x_1,\dots,x_n)}$$についてとる。こうして定義された $${\rho}$$ は距離関数である。 $${\rho(x,y)\ge 0}$$ , $${\rho(x,y)=\rho(y,x)}$$ は良い。 $${\rho(x,y)\iff x=y}$$ を証明する。
$${\Rightarrow}$$ $${\rho(x, y)=0}$$ なので、任意の $${i}$$ に関して $${\sigma(x_{i-1}, x_i)=0}$$ である。したがって、任意の $${i}$$ に関して $${x_{i-1}^{-1}x_i\in N_i\backslash N_{i+1}}$$ 。よって、 $${x_{i-1}^{-1}x_i=e}$$ であり、 $${x=y}$$。
$${\Leftarrow}$$ $${x=y}$$ で、 $${x^{-1}y=e}$$より任意の $${k}$$ に対して $${x^{-1}y=e\in N_k\backslash N_{k+1}}$$ 。よって、 $${\rho(x,y)=0}$$ 。
三角不等式を証明する。 $${x,y,z\in G}$$ と $${\epsilon >0}$$ を勝手に与えると、 $${x_0,\dots, x_n, \dots, x_m \ (x_0=x, x_n=y, x_m=z)}$$ を適当に選んで、

$$
\rho(x,y) > \rho(x_0,x_1)+\dots+\rho(x_{n-1}, x_n)-\frac{\epsilon}{2}
$$

$$
\rho(y,z) > \rho(x_n,x_{n+1})+\dots+\rho(x_{m-1}, x_m)-\frac{\epsilon}{2}
$$

とすることができる。ゆえに

$$
\rho(x,y)+\rho(y,z)>\displaystyle\sum_{i=1}^{m}\sigma(x_{i-1}, x_i) - \epsilon \ge \rho(x,y) - \epsilon
$$

$${\epsilon}$$ は任意であるから、

$$
\rho(x,z)\le \rho(x,y) + \rho(y,z)
$$

また、 $${\rho(ax,ay)=\rho(x,y)}$$ となることは、 $${\sigma(ax, ay)=\sigma(x,y)}$$ からわかる。
最後に、 $${\rho}$$ による位相が $${G}$$ の当初の位相と一致することを他方の位相の近傍系がもう一方の位相の近傍系に一致することを示すことで示す。それには

$$
(1) x^{-1}y\in N_k \Rightarrow \rho(x,y)\le \frac{1}{2^k}
$$

$$
(2) x^{-1}y \notin N_k \Rightarrow \rho(x,y)\ge \frac{1}{2^k}
$$

を示せば十分である。

(1) の証明: $${x^{-1}y\in N_k}$$ とすれば、 $${\rho}$$ の定義から、 $${\rho(x,y)\le \sigma(x,y)\le\frac{1}{2^k}}$$。

(2) の証明: $${x^{-1}y\notin N_k}$$ とする。 $${\rho(x,y)>\frac{1}{2^k}}$$ を示すためには、 $${x=x_0,x_1,\dots, x_{n-1}, x_n=y}$$ をみたす任意の有限個の点について

$$
\displaystyle\sum_{i=1}^n \sigma(x_{i-1}, x_i)\ge \frac{1}{2^k}
$$

を証明すればよい。帰納法により証明する。 $${n=1}$$ のとき、 $${x^{-1}y\notin N_k}$$ ならば $${x^{-1}y\in N_{i} \ (i\le k-1)}$$ なので、 $${\sigma(x,y)\ge\frac{1}{2^k}}$$ 。次に $${p\le n-1}$$ であるすべての $${p}$$ に対して、 $${x_0^{-1}x_p\notin N_k}$$ ならば、

$$
\displaystyle\sum_{i=1}^p \sigma(x_{i-1}, x_i)\ge\frac{1}{2^k}
$$

が成り立つと仮定する。 $${x=x_0, x_1, \dots, x_n=y}$$ とし、 $${q}$$ を $${x_0^{-1}x_q\notin N_{k+1}}$$ となるような最小の添え字 $${(1\le q\le n)}$$ とする。そこで

$$
x=x_0, \ x_{q-1}, \ x_q, \ x_n=y
$$

なる有限個の点を考えれば、帰納法の仮定により

$$
\sigma(x_0, x_{q-1}) + \sigma(x_{q-1}, x_q) + \sigma(x_q, x_n) \ge \frac{1}{2^k}
$$

($${q=n}$$ のときは、 $${n=1}$$ の場合を使い、 $${q<n}$$ のときは帰納法の仮定を用いる)
また、 $${q}$$ の定義から、 $${x_0^{-1}x_{q-1}\in N_{k+1}}$$ であるから、

$$
\sigma(x_0, x_{q-1})\le \frac{1}{2^{k+1}}
$$

(どこで使っている?)

したがって、

$$
x_{q-1}^{-1}x_q\notin N_{k+1}, \ x_q^{-1}x_n\notin N_{k+1}
$$

のどちらかが成り立つ。実際、仮に $${x_{q-1}^{-1}x_q\in N_{k+1}}$$ かつ $${x_q^{-1}x_n\in N_{k+1}}$$ であれば、

$$
x^{-1}y=x_0^{-1}x_n=(x_0^{-1}x_{q-1})\cdot(x_{q-1}^{-1}x_q)\cdot(x_q^{-1}x_n)\in N_{k+1}^3\subset N_k
$$

となって矛盾。
そこでまず $${x_{q-1}^{-1}x_q\notin N_{k+1}}$$ とすれば

$$
\sigma(x_{q-1}, x_q)\ge \frac{1}{2^k}
$$

したがって、

$$
\displaystyle\sum_{i=1}^n \sigma(x_{i-1}x_i)\ge \frac{1}{2^k}
$$

また、 $${x_q^{-1}x_n\notin N_{k+1}}$$ とすれば、 $${{x_0,x_1,\dots,x_n}}$$を

$$
x=x_0, \dots, x_q, \dots, x_n=y
$$

の形に分解して、帰納法の仮定から

$$
\sigma(x_0,x_1) + \dots + \sigma(x_{q-1}, x_q)\ge \frac{1}{2^{k+1}}
$$

$$
\sigma(x_q,x_{q+1})+\dots+\sigma(x_{n-1},x_n)\ge \frac{1}{2^{k+1}}
$$

2番目の不等式は、 $${j=q+1,\dots, n-1}$$ で、

$$
x_qx_j = x_qx_n^{-1}x_nx_0^{-1}x_0x_j\notin (N_{k+1})\subset N_k
$$

からの結果。
よって、次の結果が得られる。

$$
\displaystyle\sum_{i=1}^n\sigma(x_{i-1}, x_i)\ge 2\times \frac{1}{2^{k+1}}=\frac{1}{2^k}
$$

おわりに

少し長くなってしまいましたね。お疲れ様です。こんなところまで見ていただいてありがとうございます。
ところで先日友人から、見えている世界が違う、と言われましたが、とんでもない。むしろこのようなことばかり考え視野が狭く、盲目になった次第です。いまここにいる自分は、盲目なりに、斯様な知識をもとに細い光をたどってきた結果、といったところでしょうか。

参考

[1] 丸山徹, "群上の調和解析", 丸善出版, 2023
[2] 松坂和夫, "集合・位相入門", 岩波書店, 1968(初版)
[3] 大矢浩徳, "フェルマーの小定理について"
Fermat.pdf (hironorioya.github.io)

この記事が気に入ったらサポートをしてみませんか？