
自然数の二乗平均平方根でのつながりを調べてみた話
二乗平均平方根とは
突然ですが、$${p}$$一般化平均という単語をご存じでしょうか。これは
$$
E_p (v_1,\dots,v_n) \equiv \left(\frac{v_1^p+v_2^p+\dots+v_{n-1}^p+v_{n}^p}{n}\right)^{1/p}
$$
で定義される量で、普通の平均の拡張になっています。例えば$${p=1}$$の時、上の式は
$$
E_1 (v_1,\dots,v_n) = \frac{v_1+v_2+\dots+v_{n-1}+v_{n}}{n}
$$
となるのでよく見る普通の平均(相加平均)を再現し、$${p\to 0}$$の極限では
$$
\lim_{p\to 0} E_p (v_1,\dots,v_n) = \left( v_1\times v_2\times\dots\times v_{n}\right)^{1/n}
$$
と、相乗平均を再現できます。
では$${p=2}$$の時はどうなるでしょうか。計算すると
$$
E_2 (v_1,\dots,v_n) = \sqrt{\frac{v_1^2+v_2^2+\dots+v_{n-1}^2+v_{n}^2}{n}}
$$
となります。これが二乗平均平方根と呼ばれているもので、今回扱う重要な平均になります。具体的にいくつかの整数の組の二乗平均平方根を計算してみると
$$
E_2 (1,2)=\sqrt{\frac{1^2+2^2}{2}}=\sqrt{\frac{5}{2}} \\
E_2 (1,7)=\sqrt{\frac{1^2+7^2}{2}}=5 \\
E_2 (3,4,5)=\sqrt{\frac{3^2+4^2+5^2}{3}}=\sqrt{\frac{50}{3}} \\
$$
となります。たまに結果が整数になりますが、基本的には平方根が残ります。
今回興味があるのは平均が自然数になる$${(1,7)}$$のような自然数の組です。これを調べたけど欲しい結果が得られなかったなぁという話です。
この平均と3×3平方数魔方陣との関係
ではそもそもなぜこの平均を考えたのかというと、3×3平方数魔方陣の条件式に深くかかわっているからです。平方数魔方陣についてはひとつ前の記事
で紹介していますが、ここでも軽く紹介することにすると、
$$
\begin{array}{|c|c|c|} \hline
A^2 & B^2 & C^2 \\ \hline
D^2 & E^2 & F^2 \\ \hline
G^2 & H^2 & I^2 \\ \hline
\end{array}
$$
のようにすべての要素が平方数になっている3×3の数のまとまりで、かつ魔方陣になっている(つまり$${A^2+B^2+C^2=D^2+E^2+F^2=\cdots}$$)ものを指します。そしてこのような相異なる自然数の組$${(A,B,\dots,I)}$$が存在するかは未解決問題になっているそうです。
この9つの自然数の関係式(魔方陣になるための条件式)は次のように書き換えることができます。
$$
A=\sqrt{\frac{F^2+H^2}{2}} \qquad= E_2(F,H)\\
C=\sqrt{\frac{H^2+D^2}{2}} \qquad= E_2(H,D)\\
I=\sqrt{\frac{D^2+B^2}{2}} \qquad= E_2(D,B)\\
G=\sqrt{\frac{B^2+F^2}{2}} \qquad= E_2(B,F)\\
E=\sqrt{\frac{B^2+H^2}{2}} \qquad= E_2(B,H)\\
E=\sqrt{\frac{D^2+F^2}{2}} \qquad= E_2(D,F)
$$
つまり、魔方陣になるための条件式は二乗平均平方根を使って表すことができ、したがって全成分が平方数になるためには右辺にあるそれぞれの平均が自然数であることが必要だということができます。より正確には、3×3平方数魔方陣を構成できる必要十分条件は
$${E_2 (F,H),E_2 (H,D),E_2 (D,B),E_2 (B,F),E_2 (B,H),E_2 (D,F)}$$が自然数である
$${E_2 (B,H)=E_2 (D,F)}$$である
の二つを満たす自然数$${F,H,D,B}$$が存在することです。
そこで、少なくとも一つ目の条件を満たす組はどのようなものかを考えて二乗平均平方根を詳しく調べることにしたのです。
どのような数の組の二乗平均平方根が自然数になるのか。
では、具体的に二乗平均平方根が自然数になる数の組み合わせを探してみましょう。
一番簡単な例は同じ数同士です。というのも明らかに$${a=E_2(a,a)}$$だからですね。今回は$${F,H,D,B}$$がすべて異なる前提なのでこの状況は考えないようにします。
次に、ある自然数$${x}$$を考えて、それよりも小さい別の、$${E_2(x,y)}$$が自然数であるような自然数$${y}$$が存在するかを考えてみましょう。実は実際に試してみるとすぐに次の組が見つかります。
$$
(x,y)=(7,1),\qquad E_2(7,1)=\sqrt{\frac{7^2+1^2}{2}}=5
$$
さらに探索すると上に続いて次の組がどんどん出てきます。
$$
(x,y)=(7,1),\qquad E_2(7,1)=5 \\
(x,y)=(14,2),\qquad E_2(14,2)=10 \\
(x,y)=(17,7),\qquad E_2(17,7)=13 \\
(x,y)=(21,3),\qquad E_2(21,3)=15 \\
(x,y)=(23,7),\qquad E_2(23,7)=17 \\
(x,y)=(28,4),\qquad E_2(28,4)=20 \\
(x,y)=(31,17),\qquad E_2(31,17)=25 \\
(x,y)=(34,14),\qquad E_2(34,14)=26 \\
(x,y)=(35,5),\qquad E_2(35,5)=25 \\
\vdots
$$
当たり前ですがある$${(x,y)}$$の組が見つかると、二つに同じ数をかけたものも条件を満たします。なので$${x}$$と$${y}$$が互いに素なものに限って、さらに形式を表に変えて改めて列挙すると
$$
\begin{array}{cc|c} \hline
x & y & E_2(x,y) \\ \hline
7&1&5\\
17&7&13\\
23&7&17\\
31&17&25\\
41&1&29\\
47&23&37\\
49&31&41\\
71&49&61\\
73&17&53\\
79&47&65\\
89&23&65\\
97&71&85\\
103&7&73\\
113&41&85\\
119&41&89\\
119&79&101\\
127&97&113\\
137&7&97\\
151&31&109\\
161&73&125\\
161&127&145\\
167&119&145\\
191&89&149\\
193&17&137\\
199&161&181\\
\vdots & \vdots & \vdots \\ \hline
\end{array}
$$
となります。
これを眺めていると、なにか規則性がある感じがしませんか。$${x}$$に注目すると、まず$${7,17,23,31,\dots}$$と素数が並び、初めて出てくる合成数は$${49=7^2}$$と最初の素数$${7}$$の二乗になっています。そしてまた素数が続き、次の合成数は$${119=7\times 17}$$そしてまた素数が続いて次の合成数は$${161=7 \times 23}$$、そしてさらに素数が…と。そしてこの素数も何か規則性がありそうです。
実はここに出てくる素数はすべて8で割った余りが$${\pm 1}$$である素数(A001132 - OEIS)になっており、合成数はすべてこれらの素数同士の積になっています。$${y}$$のほうも同様ですね。一方、$${x}$$と$${y}$$のペアに規則性があるかは…よくわかりませんが一応$${y=1}$$の場合の$${x}$$はA002315 - OEISに載っている数っぽいです($${y=7}$$の時の$${17,23,103,137,601,\dots}$$、$${y=17}$$の時の$${31,73,193,431,1127,\dots}$$は載っていなかったです。何か規則性があるのでしょうか)。
そして、それぞれの$${x}$$に対応する$${y}$$の数は素因数分解したときの素数の種類に等しそうです。例えば$${7\to1\text{個},49=7^2\to1\text{個},161=7\times 23\to2\text{個}}$$といった感じです。
ペアを図にしてみる
こうして二乗平均平方根$${E_2(x,y)}$$が自然数になる自然数の組$${(x,y)}$$をある程度絞ることができました。あとはひたすら$${F,H,D,B}$$を見つけるだけです。しかし、いちいち数式や表を書くのではわかりにくいので、この関係性を図にしてみましょう。例えば$${(7,1)}$$のペアを

と点と線で表すことにしましょう。また、もし二つの数の大小関係を明示したいときは

と矢印を使うことにします。
この表示を使って今までの関係を表すと、例えば$${128}$$以下の数たちに対して

のように線をつなぐことができます。あるいは大小関係を明示して

ともかけます。ちなみに注意点として、今回は互いに素なペアしか注目していないので$${(49,7)}$$のペアが図からは省かれています。試しに互いに素なペア以外のものも出力してみると次のような感じになります。
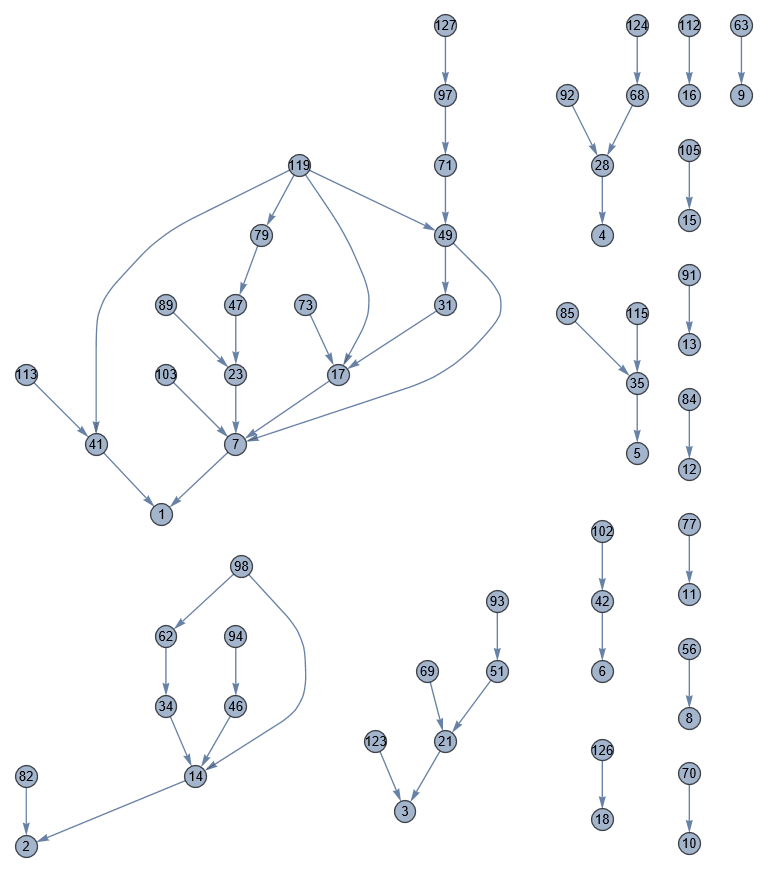
まあ…、左上以外は重要ではないのですが。
四面体を探してみる
さて、私たちの目的は$${E_2 (F,H),E_2 (H,D),E_2 (D,B),E_2 (B,F),E_2 (B,H),E_2 (D,F)}$$が自然数になるような$${F,H,D,B}$$の組を探すことでした。これをこの図を用いて表すと

となります。つまり、これと同じ、四面体のような形を図の中に見つけることができれば目標達成というわけです。ただまあ、上の図を見ると四面体はおろか三角形すら見つかりません。
実は、任意の2つの二乗平均平方根が自然数になるような組$${(x,y,z)\scriptsize\text{(つまり}E_2(x,y),E_2(y,z),E_2(z,x)\text{が自然数)}}$$は$${329=7\times 47}$$まで考えた時に初めて出てきます。その時のグラフは

です(ちょっと小さめになってしまうのでよく見たい方は拡大してください)。$${(x,y,z)=(329,191,89)}$$ですね。試しに$${329}$$の周りだけ書けば

と、より分かりやすく三角形ができていることがわかります。またほかにも三角形は$${527=17\times31,1081=23\times 47,3689=7\times 17 \times 31}$$などのペアを考えた時にも出てきます。

さらに$${7567=7\times23\times47}$$では

と、二つの三角形が合体したような図形も出てきます。この調子で数の上限を大きくしていき、四面体を探してみました。
探索結果:見つからなかった
しかし、いくら数を大きくしても四面体のような形は現れませんでした。$${2^{20}}$$ぐらいまでは全探索し、複数の素数をかけて大きな数も手あたり次第探索しましたが見つけられませんでした。おそらく型が関係していると思いますが$${2^{31}}$$を超えたあたりから急に計算時間が長くなり、$${2^{31}}$$以上の数を探索するのは結構難しいのでひとまず探索をここで終えることにします。最後に、探索した最大の数$${12,916,513,351=7\times 17 \times 23 \times 31 \times 41 \times 47 \times 79}$$の図を出して終わりにしたいと思います(ただし見にくかったので中心と三角形を作らない数を外し、矢印ではなく線で表示しています)。

実は探索しているとき、この表示での三角形(つまり元々言っていた四面体)はおろか、この表示での多角形を一度も見かけませんでした。もしかしたら何か理由があるのかもしれません。
