
開成中学の入試問題(算数)をOBが解いてみて解説する(2019年度)
中学入試、終わりましたね。
ということで解いてみました!ちょっと時期が遅れちゃいましたが......。
設問ごとに丁寧丁寧丁寧に解説したあと、最後の総括で実践的なこと(本番ではいかに点数をとるか)を話していきます。
※出典:開成中学 2019年 算数入試問題
大問1

◎解法
⑴
旅人算の問題です。ということは、まずは図を書きましょう。わかってる情報(K君の速度)も書き込みます。

さて、ここで一つ問題点があります。それは、速さ以外の情報が不足していることです。
情報が足りずに解けないときは、丸数字を置くことで解くために足りない情報を埋めることが中学受験算数の基本でしたね。
ここでは、「自宅からおばさんの家までの距離」と「かかった時間」の2つが足りない情報です。
※「速さの公式:速さ×時間=距離」の3つのキーのうち、速さの情報はあるが距離と時間の情報がほぼない。
「K君が1人で運んだ場合」に「かかった時間」を⑯分と置けば、
「実際」に「かかった時間」は15/16の⑮分、
「自宅からおばさんの家までの距離」は 毎分60m × ⑯ = (960)m だと導き出せます。
※(960)は丸数字の960です。
ここまでの情報を図に書き込みます。※下図の赤字

さらに、K君がスイカを1つ運び終えるまでにかかった時間は、距離(960) ÷ 分速80m = ⑫分だとわかります。
すると、設問にある
「K君が一度目におばさんの家についてから、二度目におばさんの家につくまでの時間」は、⑮分 - ⑫分 = ③分 だとわかります。
※ここまでの情報は上図の青字
図より、③ ÷ ⑯ = 3/16 が答え
⑵
図の一部に注目して考えます。

ここの往復でかかった合計時間は、⑴より③分でしたね。
また、「おばさんの家を出てからS君に出会うまでにかかった時間」と「S君に出会ってからおばさんの家に着くまでにかかった時間」は、分速の逆比から80:100、つまり4:5とわかります。
※速さの公式:速さ×時間=距離。距離は同じなので速さと時間は逆比になる。
この往復でかかった合計時間が③分ですから、
「おばさんの家を出てからS君に出会うまでにかかった時間」が(4/3)分
「S君に出会ってからおばさんの家に着くまでにかかった時間」が(5/3)分
となります。※上図の青字
ここまで分かればあとは簡単です。
求める距離は、分速100m × (4/3)分 = (400/3)mなので、
これを全体の距離(960)mで割って5/36 が答え
⑶
ボーナス問題。
SくんがK君に出会うまでの距離は、⑵の答えを用いて
(960)m × (1 - 5/36) = (2480/3)m
SくんがK君に出会うまでの時間は、当たり前ですがK君がS君に出会うまでの時間と同じなので、K君がS君に出会うまでの時間を求めます。
⑫分 + (4/3)分 = (40/3)分
S君が進んだ距離とS君がかかった時間がわかったので、速さの公式に当てはめれば速さが出ます。
速さ = 距離 ÷ 時間
速さ = (2480/3)m ÷ (40/3)分 = 分速62m が答え
◎ひとこと
旅人算をマスターしていれば簡単に解ける。ぜひ完答したい問題。
丸数字を置いたあと、丁寧に図に情報を書き込んでいくだけで満点が取れる。
大問2
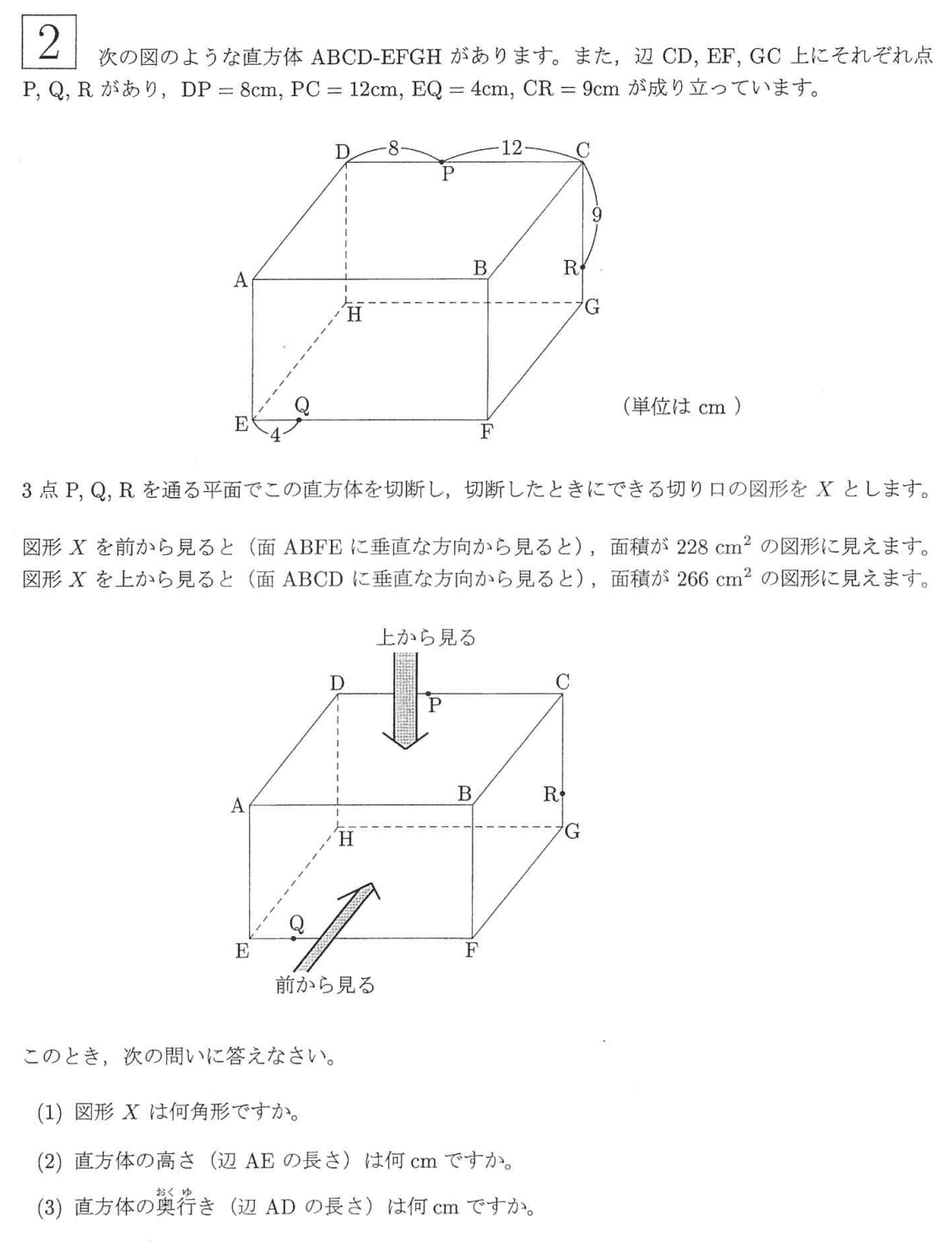
◎解法
⑴
直方体を切る問題は、向かい合う面の切り口は平行線というポイントを押さえます。
まずはPRに平行となるように直線QSを描きます。(下図の赤線)
次はPQからQSに包丁を差し込むとどうなるか、イメージしながら他の直線を考えて描きます。(下図の青線)
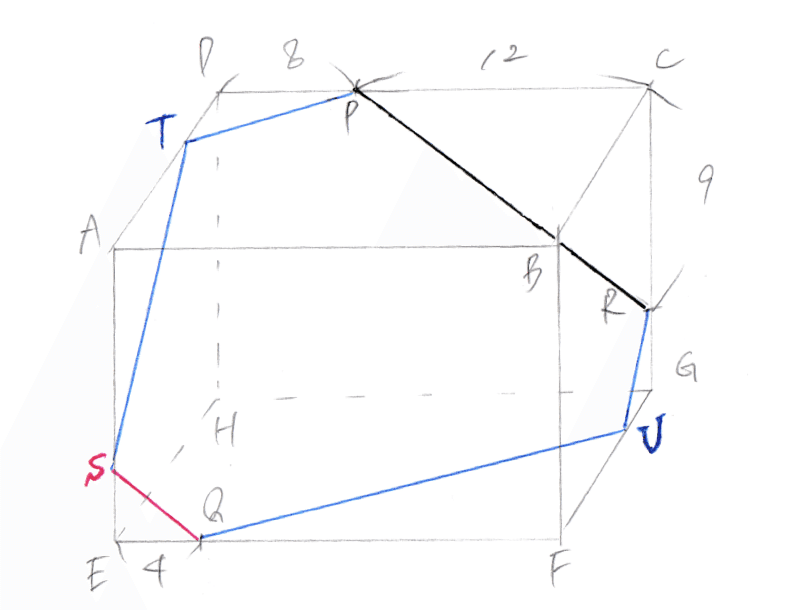
六角形 が答え
※1つの面に存在する直線(切り口)は1つまで、ということにも注意するとイメージしやすいです。
1つの面に2つ以上の切り口(直線)をつくることは、包丁を一度通すだけでは不可能ですよね?
⑵
長さを求めるのは辺AEなので、辺AEを含む「前から見た場合の図形」から考えていきます。
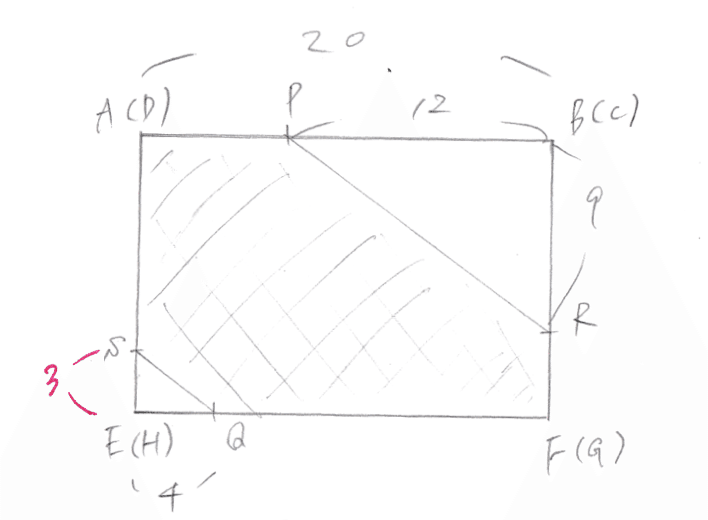
まず、SQとPRが平行なことから、三角形SEQと三角形RPQは相似ですね。
よってSE = 3 がわかります。
※斜線部が、前方から見たときの図形(228㎠)
面AEFBの面積を□と置くと、
□ - 三角形EQS - 三角形CPR = 228
つまり
□ - 6 - 54 =228
□=288
AB = 20なので
AE = 288 ÷ 20
= 14.4cm が答え
⑶
まずは辺ADを含む「上から見た場合の図形」を考えます。

TPとUQは平行なので、三角形と三角形は相似です。
よって辺と辺の比は8:16、つまり1:2ですね。
なのでDTの長さを①、UBの長さを②と置いておきましょう。
しかし、これだけの情報ではADの長さを求めることはできませんね。
ここで、新たな情報を手に入れるために、切断面の線は伸ばすという定石を使います。
実際に伸ばしてみるとこうなります。

さて、三角形XYHと三角形XHZについて考えてみましょう。
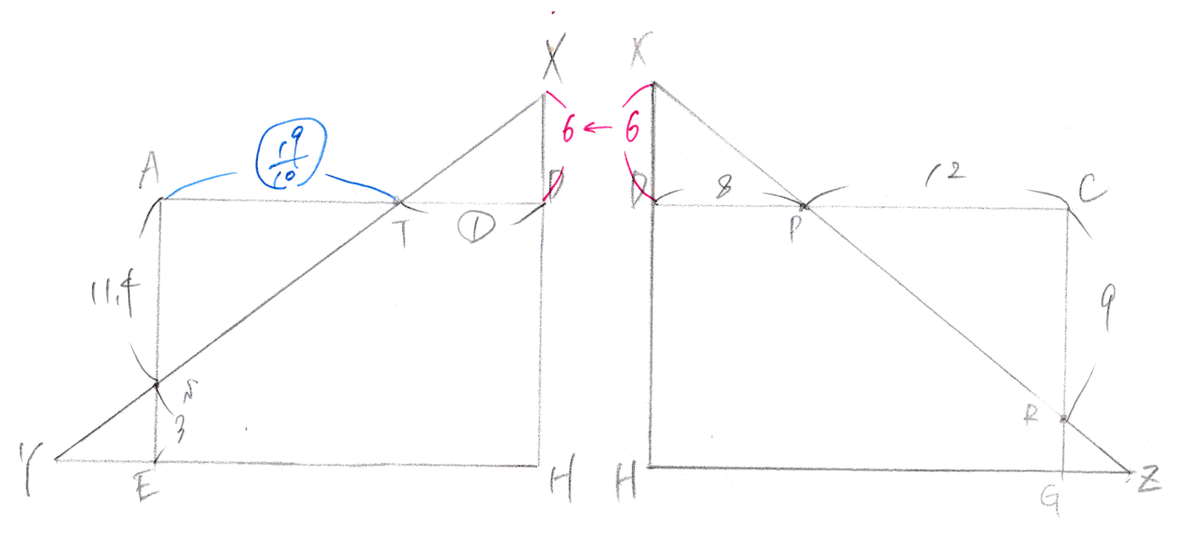
まずは長さの情報が多い三角形XHZから考えていきましょう。※右の図
三角形PRCと三角形PXDは相似です。よって比を使って XD = 6cm だとわかりますね。
ここで左の図にうつりましょう。
まずは増えた情報「XD=6cm」を書き込みます。
三角形TDXと三角形TASは相似なので、比を使って TA = (19/10) だとわかりますね。
ここでもとの「上から見た場合の図形」に戻ります。

TA = (19/10) でしたが、分数だと面倒なので丸数字を全て10倍してしまいましょう。TAは[19]となります。※[ ]は四角数字
すると DA = [29] となり、この[29]が何cmかを求めれば、その長さが答えになりますね。
四角形DABC - 三角形DTP - 三角形UQB = 266
つまり
[580] - [40] - [160] = 266
[380] = 266
[1] = 0.7
よって
[29] = 0.7 × 29
= 20.3cm が答え
◎ひとこと
立体の切断面の問題をマスターしていれば、(2)までは簡単に解ける。
(3)は難しいが、切断面の線は伸ばすというポイントが身についていれば解けるはず。
大問3


◎解法
⑴図1
解法1
図に書き込みます。道順の問題の定石です。

図より10通り が答え
解法2
平らにして考えます。

Aから上に2回、右に3回進めばBにたどりつきます。
「上」と書かれた2つの球と、「右」と書かれた3つの球を一列に並べる並べ方を考えて、
5 × 4 ÷ 2 = 10通り が答え
※例えば球の並び方が「上 右 上 右 右」ならば、この順に進めばBにたどりつきます。こちらの解き方も道順の問題の定石です。
※球の並べ方の問題を解く方法については、またいつか記事にしようと思ってます。
⑴図2
図に書き込みます。

※図1の解法2のように解くことも一応可能ですが、場合分けが面倒なのでこの方法で解く方が楽です。
図より10通り が答え
⑵図3
どの点で左に進むか考えます。

①で左に進むことはできない。
②で左に進む場合
・Aから②まで:1通り
②から左に進んで①に着いて、
・①からBまで:4通り
よって1 × 4 = 4通り
③で左に進む場合
・Aから③まで:1通り
③から左に進んで②に着いて、
・②からBまで:3通り
よって1 × 3 = 3通り
④で左に進む場合
・Aから④まで:1通り
④から左に進んでに③着いて、
・③からBまで:2通り
よって1 × 3 = 2通り
⑤で左に進むことはできない。
⑥で左に進む場合
・Aから⑥まで:1通り
⑥から左に進んで⑤に着いて、
・⑤からBまで:2通り
よって1 × 2= 2通り
⑦で左に進む場合
・Aから⑦まで:3通り
⑦から左に進んで⑥に着いて、
・①からBまで:1通り
よって1 × 3 = 3通り
⑧で左に進む場合
・Aから⑧まで:4通り
⑧から左に進んで⑦に着いて、
・⑦からBまで:1通り
よって1 × 3 = 4通り
足し合わせて合計18通り が答え
⑵図4

図3と同様に、どの点で左に進むか考えます。
① 1 × 10 = 10通り
② 1 × 6 = 6通り
③ 1 × 3 = 3通り
④ 2 × 4 = 8通り
⑤ 3 × 3 = 9通り
⑥ 4 × 2 = 8通り
⑦ 3 × 1 = 3通り
⑧ 4 × 1 = 6通り
⑨ 10 × 1 = 10通り
足し合わせて合計64通り が答え
◎ひとこと
⑴はサービス問題なので、とりあえず⑴は正解したい。
⑵どこの点で左に進むか、がポイント。解法が思いつかなければ後回しにするのが良い。
大問4


◎解法
⑴
問題文をよく読んで書くだけです。簡単にまとめると、
・♡は奇数、♣︎は偶数。
・最初は全員、奇数と偶数のペアを持っている。
・持っているペアのうち、大きい方の数を反時計回りに渡す。小さい方の数はキープ。
・持っているペアが両方偶数、または両方奇数になったらその人はアウト。
答えを書き終えたら、ミスしていないか一度見直しましょう。
答えは下図

※キープされる「小さい方の数字」を先に全て書いてから、右隣に渡される「大きい方の数字」を書いていくとミスしにくいです。
⑵
(a)

(x)(上図の赤字・青字)
まずは(ク)について考えます。
(ケ)に3がない、つまり(ク)に3があるということです。
Cは(ク)の時点ではアウトにはなっていないので、(ク)の3のペアは偶数。
また、Cの3が次の手順でDに渡されるから、3のペアは3より小さい。
以上の2つから、3のペアは2しかありえません。
23 が答え
(y)(上図の赤字・緑字)
次に、(ケ)について考えます。
(ケ)に3がない、つまり(ケ)には8があるということです。
Cは(ケ)の時点ではアウトになっていないので、(ク)の8のペアは奇数。
また、Dの8は次の手順でキープされるから、8のペアは8より大きい。
以上の2つから、8のペアは9しかありえません。
89 が答え
(z)
「最初は全員、奇数と偶数のペアを持っている」というルールを活用します。
Cで2がキープされた場合と、3がキープされた場合に分けて考えます。

Cで2がキープされた場合、そのペアは「奇数かつ2より大きい」。
また、2のペアは(ケ)にある8か9のどちらかなので、奇数である9がペア。
よって29 (これはすでに問題文に書かれています。)

Cで3がキープされた場合、そのペアは「偶数かつ3より大きい」。
また、2のペアは(ケ)にある8か9のどちらかなので、偶数である8がペア。
よって28 が答え
(b)
手順①
「最初は全員、奇数と偶数のペアを持っている」のルール。
それと、一度回した段階では誰もアウトしなかった、つまり「一度回した段階でも、全員奇数と偶数のペアを持っている」という事実。
この2つの情報を図に書き込むとこんな感じになります。

手順②
図のようになるためには、「全員が偶数を回す」または「全員が奇数を回す」必要があります。
ここで、一番大きい数Tは必ず回されることに気づきます。Tは偶数だから、「全員が偶数を回す」の方が正しいとわかります。
手順③
全員が偶数を回すので、偶数の中で一番小さい「2」も当然回されます。
2が回されるということは、2のペアは2よりも小さい奇数の「1」以外ありえません。よって{1,2}のペアが決定します。
手順④
全員が偶数を回すので、偶数の中で二番目に小さい「4」も当然回されます。
4が回されるということは、4のペアは4よりも小さい奇数の「1」または「3」以外ありえません。1はもう2のペアとして使われているので、4のペアは3。
よって{3,4}のペアが決定します。
全員が偶数を回すので、偶数の中で三番目に小さい「6」も当然回されます。
6が回されるということは、6のペアは6よりも小さい奇数の「1」または「3」または「5」以外ありえません。1は2と、3は4とペアとして使われているので、6のペアは5。
よって{5,6}のペアが決定します。
同じように8、Tについても考えると、ペアは全部でこんな感じになります。
{1,2} , {3,4} , {5,6} , {7,8} , {9,T}
だから答えは「偶数の方が奇数より1大きい」、つまり
「スペードの方がハートより1大きい」 が答え
(c)

(ク)に8、(ケ)に3があることがすでわかっているので、そこから考えます。
最初は全員が偶数を回していて、奇数をキープしているので、
8は(イ)に、3は(エ)にあります。
そして、問題(z)の答え「偶数の方が奇数より1大きい」より、(イ)は{7,8}のセット、(エ)は{3,4}のセットだとわかります。(ここまで上図)
次に、どこから求めるか考えましょう。
(ク)が、解くために使える情報が一番多そうですね。ということで(ク)から求めていきます。

(ク)の8のペアは奇数の1、5、9のどれか。(3、7はすでに使われています。)
まずは1が入っていると仮定して考えていきます。

1は最小の数だから、ずっとその場にキープするので、(ウ)には1が入り、(ウ)は(1,2)のペアとなります。
次に、(ウ)からは2が移動するため(ケ)は(2,3)のペアとなって、この次は3がEに移動してしまうことになりますが、これはDが(3,8)のペアで勝つことと話が合いません。
よって1はボツですね。
次に9が入っていると仮定して考えていきます。

8よりも9の方が大きいので、9がDに回されてしまいます。
Dは(3,8)のペアで勝つことになっているので、話が合いません。
これで残った5が(ク)に入ることがわかりましたね。
※仮定する数字ですが、極端なものから考えていくことが重要です。
今回は1、5、9のうち1が「一番小さい数」ということで最も極端、9が「最も大きい奇数」ということで次に極端だったので、1→9→5の順で考えていくことにしました。
さて、(ク)が58のペアだとわかったので、そこからすぐにわかる(ウ)のペアも求めておきましょう。
8は(イ)にあるので(ウ)には5が入ります。よって(ウ)のペアは{5,6}ですね。
さらに(ウ)から6が移動することから、(ケ)は{3,6}のペアで決定です。
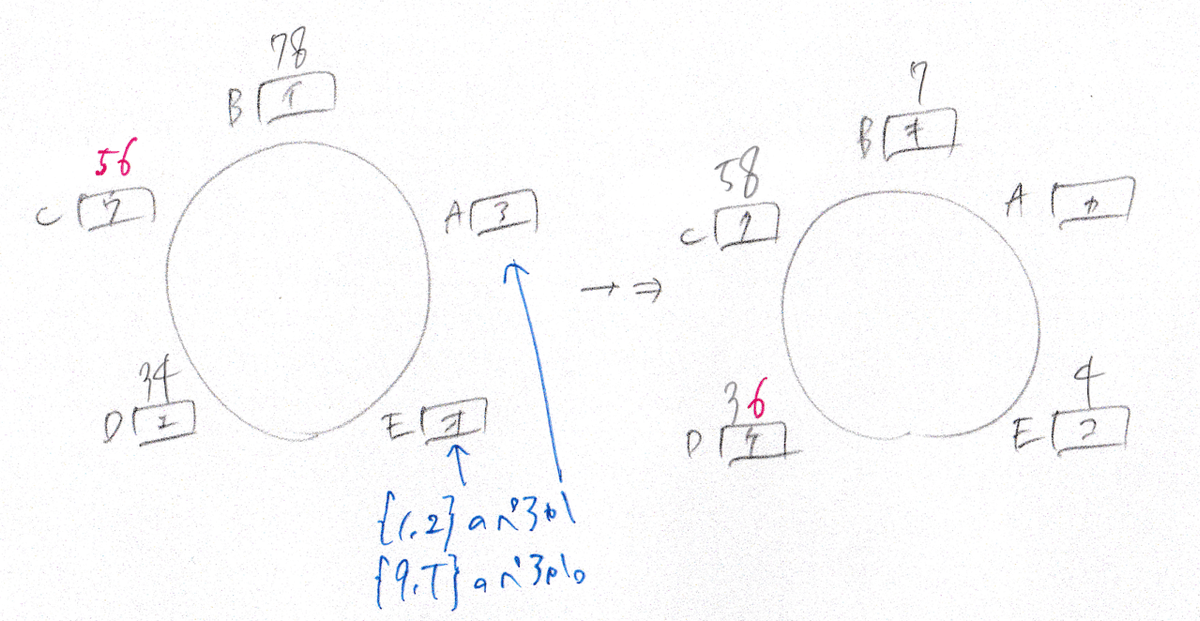
さて、残ったA,Eについて考えます。残ったペアは{1,2}と{9,T}の二つなので、Aに{1,2}が入るパターンとAに{9,T}が入るパターンの両方を当てはめてみて、どちらが正しいか判断しましょう。
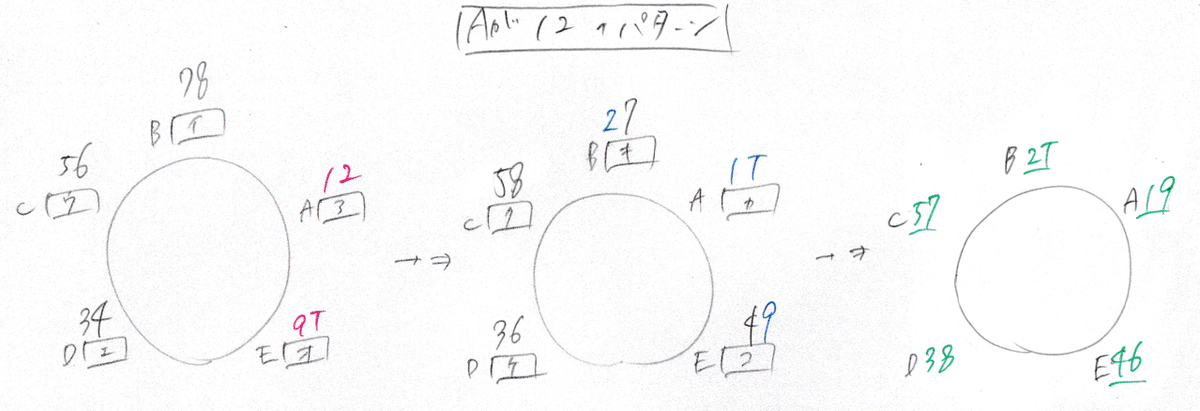

ということで、アに{1,2}、オに{9,T}が入るパターンが正しいことがわかりました。
お疲れ様でした。ア〜コまで、答えはこちらです。

◎ひとこと
とりあえず問題文を読みこんで⑴だけは解く。
⑵以降は頭を使う問題。特に(b)以降はかなり難しい。自分も解くのに1時間ほどかかった。試験では捨てるべき問題。
〜〜〜
総括
問題の難しさは、
(易しい) 大問1<大問3<大問2<大問4 (難しい)
という感じ。
大問1は確実に完答、大問2と大問3のどちらかを完答、残った2つの大問は半分ずつ正解するのが理想。
開成の算数は7割とれればなかなか良い感じ。これで点数はちょうど7割程度となる。
(まあ自分は全部解けたんですけどねっ!!!)
〜〜〜
いかがでしたか?
話が変わりますが、これからnoteで中学受験向けの記事を書いていこうと思っています。編集途中ですがこんな感じです↓

ということなので、来年中学受験!再来年中学受験!って方ぜひフォローしていただけると嬉しいです!
中学受験問題の解説ブログって難しいものが多いと思っていて。自分はわかりやすい記事を書いていくので期待していてください!笑
ではまたお会いしましょう〜!
追記
質問やリクエスト、感想やアドバイスなど、お気軽にこちらへどうぞ!
kkunnmail@gmail.com
追記
YouTubeにも解説動画を投稿しようと思っています。
