＜学習シリーズ＞微分方程式の解法：反復法のJacobi(ヤコビ)法をPythonで学ぶ

KIYO

2022年12月17日 11:22

１．概要

１－１．緒言

　本記事は”学習シリーズ”として自分の勉強備忘録用になります。

　偏微分方程式の解法の中で反復法は下記手法がありますが、今回は最もシンプルなヤコビ（Jacobi）法を説明します。

ヤコビ法：求める変数の計算がすべて完了したらまとめて更新する
ガウス・ザイデル法：更新した値を逐次的に使用していく
SOR法：ガウス・ザイデル法をさらに修正したモデル
共役勾配法

１－２．サンプル問題

　今回のサンプル問題は3つの変数と式からなる連立方程式を解きます。なお説明のしやすさを考慮して連立方程式と線形代数の２種を記載しました。

$$
a_{11}x_{1} + a_{12}x_{2} + a_{13}x_{3} = b_{1} \\
a_{21}x_{1} + a_{22}x_{2} + a_{23}x_{3} = b_{2} \\
a_{31}x_{1} + a_{32}x_{2} + a_{33}x_{3} = b_{3}
$$

$$
AX=Bより\begin{bmatrix}a_{11}x_{1} + a_{12}x_{2} + a_{13}x_{3} \\a_{21}x_{1} + a_{22}x_{2} + a_{23}x_{3} \\a_{31}x_{1} + a_{32}x_{2} + a_{33}x_{3}\end{bmatrix}=\begin{bmatrix}b_{1} \\ b_{2} \\ b_{3}\end{bmatrix}
$$

$$
A=\begin{bmatrix}a_{11} & a_{12} & a_{13} \\a_{21} & a_{22} & a_{23} \\a_{31} & a_{32} & a_{33}\end{bmatrix}, X=\begin{bmatrix}x_{1} \\ x_{2} \\ x_{3}\end{bmatrix}, B=\begin{bmatrix}b_{1} \\ b_{2} \\ b_{3}\end{bmatrix}
$$

　サンプルの数値は下記を使用します。計算すると解は$${{x1: 1, x2: 1, x3: -1}}$$となります。

$$
2x_{1} + x_{2} + x_{3} =2\\
2x_{1} +3x_{2} + x_{3} =4\\
x_{1} + x_{2} +3x_{3} =-1
$$

$$
AX=Bより\begin{bmatrix}2x_{1} + x_{2} + x_{3} \\2x_{1} + 3x_{2} + x_{3} \\x_{1} + x_{2} + 3x_{3}\end{bmatrix}=\begin{bmatrix}2 \\ 4 \\ 1\end{bmatrix}
$$

$$
A=\begin{bmatrix}2 & 1 & 1 \\2 & 3 & 1 \\1 & 1 & 3\end{bmatrix}, X=\begin{bmatrix}x_{1} \\ x_{2} \\ x_{3}\end{bmatrix}, B=\begin{bmatrix}2 \\ 4 \\ 1\end{bmatrix}
$$

[IN]
import sympy as sp
sp.init_printing()

a11, a12, a13, a21, a22, a23, a31, a32, a33 = sp.symbols('a11 a12 a13 a21 a22 a23 a31 a32 a33')
x1, x2, x3 = sp.symbols('x1 x2 x3')
b1, b2, b3 = sp.symbols('b1 b2 b3')

A = sp.Matrix([[a11, a12, a13],
               [a21, a22, a23],
               [a31, a32, a33]])
B = sp.Matrix([[b1],[b2],[b3]])
X = sp.Matrix([[x1],[x2],[x3]])

eq1 = sp.Eq(A@X, B)
display(eq1)

A[0], A[1], A[2], A[3], A[4], A[5], A[6], A[7], A[8] = 2,1,1,2,3,1,1,1,3
B[0], B[1], B[2] = 2,4,-1
display(sp.Eq(A@X, B))

sp.solve(sp.Eq(A@X, B), [x1, x2, x3])

[OUT]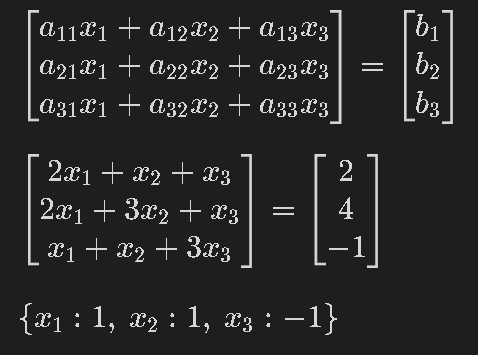

２．反復法／ヤコビ法の理解１：連立方程式Ver.

　　”直接法（LU分解やガウスの消去法）”では式変形することにより直接的に解Xを算出しました。

　反復法では式変形はせずに求めたい解Xに近似解を代入して逐次的に連立方程式を解くことで近似解を求めていきます。本章では具体的に数式を使用しながら説明します。
　計算の大きな流れは下記の通りです。

求めたい解(変数)$${x}$$に適当な初期値を与える
i行目の$${x_{i}}$$を計算する場合、それ以外の行のxを固定値として$${x_{i}}$$を求める。これを全行で実行する。
上記の計算を何回も繰り返し計算後の$${x_{i}}$$に変化がなくなった時点で計算を終了する

２－１．連立方程式の概要

　まず初めにわかりやすさを考慮して連立方程式でのヤコビ法のイメージを説明します。参考として下記の連立方程式を考えてみます。
　なおaは係数、xは求めたい解、bは定数となります。なお当たり前のことですが連立方程式を解くためには「解の数≦数式の数」ため式の行数は最低でも数式以上の数となります。

$$
A_{11}x_{1}+A_{12}x_{2}+A_{13}x_{3}+\dots+A_{1n}x_{n}=b_{1} \\ A_{21}x_{1}+A_{22}x_{2}+A_{23}x_{3}+\dots+A_{2n}x_{n}=b_{2} \\ A_{31}x_{1}+A_{32}x_{2}+A_{33}x_{3}+\dots+A_{3n}x_{n}=b_{3} \\ \vdots \\ A_{n1}x_{1}+A_{n2}x_{2}+A_{n3}x_{3}+\dots+A_{nn}x_{n}=b_{n}
$$　

　また反復計算をする前に$${x_{i}}$$に適当な(初期)値を与えます。Pythonコードでは正規分布(np.random.randn())を使用しました。（後述で初期値$${c_{i}}$$を与えていますが記号としては$${x_{i}}$$を使用していきます）

$$
\bm x =\begin{bmatrix} x_{1} & x_{2} & \dots & x_{n} \end{bmatrix} -> \bm x = \begin{bmatrix} c_{1} & c_{2} & \dots & c_{n} \end{bmatrix}
$$

２－２．１行だけで確認

　1行目の式から$${x_{1}}$$を解いてみます。xには既に（適当な初期）値を与えているため$${x_{1}}$$を求めることが出来ます（$${x_{1}}$$も初期値を与えておりますが$${x_{1}}$$を求めるときには使用せず上書きします）。

$$
A_{11}x_{1}+A_{12}x_{2}+A_{13}x_{3}+\dots+A_{1n}x_{n}=b_{1}
$$

$$
x_{1}=\frac{b_{1}-A_{12}x_{2}-A_{13}x_{3}-\dots-A_{1n}x_{n}}{A_{11}}
$$

２－３．全体で確認

　式全体で考えると下記の通りです。

　上式を各行で分解すると下記の通りです。

$$
x_{1}=\frac{1}{A_{11}}(b_{1}-A_{12}x_{2}-A_{13}x_{3}-\dots-A_{1n}x_{n})
$$

$$
x_{2}=\frac{1}{A_{22}}(b_{2}-A_{21}x_{1}-A_{23}x_{3}-\dots-A_{2n}x_{n})
$$

$$
x_{3}=\frac{1}{A_{33}}(b_{3}-A_{31}x_{1}-A_{32}x_{2}-\dots-A_{3n}x_{n})\\
\vdots
$$

$$
x_{n}= \frac{1}{A_{nn}}(b_{n}-A_{n1}x_{1}-A_{n2}x_{2}-\dots-A_{nn-1}x_{n-1})
$$

　上記より下記が確認できます。

i行目にある求めたい解$${x_{i}}$$の分母は$${A}$$成分の対角の値
構造はすべての行で同じであり分子：定数b-対角成分以外の内積の差分、分母：係数Aの対角の値

３．反復法／ヤコビ法の理解２：行列Ver.

３－１．行列式の概要

　次に行列で定式化します。$${\bm A}$$は係数行列、$${\bm X}$$は解ベクトル、$${\bm b}$$は定数ベクトルであり求めたいのは$${\bm X}$$です。

$$
\bm A \cdot \bm X = \bm bより
$$

$$
\begin{bmatrix}A_{11} & A_{12} & A_{13} \dots A_{1n} \\A_{21} & A_{22} & A_{23} \dots A_{2n} \\A_{31} & A_{32} & A_{33} \dots A_{3n} \\ \vdots & \vdots & \vdots \\A_{n1} & A_{n2} & A_{n3} \dots A_{nn} \end{bmatrix}
\begin{bmatrix} x_{1} \\ x_{2}\\x_{3} \\ \vdots \\ x_{n} \end{bmatrix}
= \begin{bmatrix} b_{1} \\ b_{2}\\b_{3}\\ \vdots \\ b_{n} \end{bmatrix}
$$

３－２．LDU分解／余剰行列R

　$${\bm A}$$は係数行列は下記の通り上三角行列U、下三角行列L、対角行列Dに分解できます。

$$
\bm A=\bm U + \bm D + \bm L =
$$

$$
\begin{bmatrix}0 & A_{12} & A_{13} \dots A_{1n} \\ 0 & 0 & A_{23} \dots A_{2n} \\ 0 & 0 & 0 \dots A_{3n} \\ \vdots & \vdots & \vdots \\ 0 & 0 & 0 \dots 0 \end{bmatrix}+
\begin{bmatrix}A_{11} & 0 & 0 \dots 0 \\ 0 & A_{22} & 0 \dots 0 \\ 0 & 0 & A_{33} \dots 0 \\ \vdots & \vdots & \vdots \\ 0 & 0 & 0 \dots A_{nn} \end{bmatrix}+
\begin{bmatrix}0 & 0 & 0 \dots 0 \\A_{21} & 0 & 0 \dots 0 \\A_{31} & A_{32} & 0 \dots 0 \\ \vdots & \vdots & \vdots \\A_{n1} & A_{n2} & A_{n3} \dots 0 \end{bmatrix}
$$

　L+Uは余剰行列Rとなるため下記の通り変形可能です。

$$
\bm A= \bm D +(\bm U + \bm L) =D +R =
$$

$$
\begin{bmatrix}A_{11} & 0 & 0 \dots 0 \\ 0 & A_{22} & 0 \dots 0 \\ 0 & 0 & A_{33} \dots 0 \\ \vdots & \vdots & \vdots \\ 0 & 0 & 0 \dots A_{nn} \end{bmatrix}+
\begin{bmatrix} 0 & A_{12} & A_{13} \dots A_{1n} \\ A_{21} & 0 & A_{23} \dots A_{2n} \\ A_{31} & A_{32} & 0 \dots A_{3n} \\ \vdots & \vdots & \vdots \\ A_{n1} & A_{n2} & A_{n3}\dots 0 \end{bmatrix}
$$

３－３．数式の解法

　前述の式を考えると行列式は下記の通りに解くことが出来ます。

$$
\bm A \cdot \bm X = \bm bより (\bm D+\bm R) \cdot \bm X = \bm b
$$

$$
\bm D \bm X+\bm R \bm X = \bm b\\
\bm D \bm X= \bm b-\bm R \bm X \\
\bm X=\bm D ^{-1}( \bm b-\bm R \bm X) \\
$$

　上記より初期値$${ \bm X _{n}}$$として次のステップにおける解$${ \bm X _{n+1}}$$は下記の通り計算できます。

$$
\bm X_{n+1}=\bm D ^{-1}( \bm b-\bm R \bm X_{n})または\bm X_{n+1}=\bm D ^{-1}( \bm b-(\bm L+\bm U) \bm X_{n})
$$

３－４．解法の検算

　くどい説明となりますが求めた数式$${\bm X_{n+1}=\bm D ^{-1}( \bm b-\bm R \bm X_{n})}$$を検算して求めたい形になっていることを確認します。

$$
\bm X_{n+1}=\bm D ^{-1}( \bm b-\bm R \bm X_{n})=
$$

$$
\begin{bmatrix} \frac{1}{A_{11}} & 0 & \ldots & 0 \\ 0 & \frac{1}{A_{22}} & \ldots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \ldots & \frac{1}{A_{nn}} \end{bmatrix}
\cdot
(\begin{bmatrix} b_{1} \\ b_{2}\\b_{3}\\ \vdots \\ b_{n} \end{bmatrix}
-
\begin{bmatrix} 0 & A_{12} & A_{13} \dots A_{1n} \\ A_{21} & 0 & A_{23} \dots A_{2n} \\ A_{31} & A_{32} & 0 \dots A_{3n} \\ \vdots & \vdots & \vdots \\ A_{n1} & A_{n2} & A_{n3}\dots 0 \end{bmatrix}\cdot \begin{bmatrix} x_{1} \\ x_{2}\\x_{3} \\ \vdots \\ x_{n} \end{bmatrix})=
$$

$$
\begin{bmatrix} \frac{1}{A_{11}} & 0 & \ldots & 0 \\ 0 & \frac{1}{A_{22}} & \ldots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \ldots & \frac{1}{A_{nn}} \end{bmatrix}
\cdot
(\begin{bmatrix} b_{1} \\ b_{2}\\b_{3}\\ \vdots \\ b_{n} \end{bmatrix}
-
\begin{bmatrix} 0 + A_{12}x_{2} + A_{13}x_{3} \dots A_{1n}x_{n} \\ A_{21}x_{1} + 0 + A_{23}x_{3} \dots A_{2n}x_{n} \\ A_{31}x_{1} + A_{32}x_{2} + 0 \dots A_{3n}x_{n} \\ \vdots \\ A_{n1}x_{1} + A_{n2}x_{2} + A_{n3}x_{3}\dots 0 \end{bmatrix}=
$$

$$
\begin{bmatrix} \frac{1}{A_{11}} & 0 & \ldots & 0 \\ 0 & \frac{1}{A_{22}} & \ldots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \ldots & \frac{1}{A_{nn}} \end{bmatrix}
\cdot
\begin{bmatrix} b_{1} - 0 - A_{12}x_{2} - A_{13}x_{3} \dots A_{1n}x_{n} \\ b_{2} -A_{21}x_{1} - 0 - A_{23}x_{3} \dots A_{2n}x_{n} \\ b_{3} -A_{31}x_{1} - A_{32}x_{2} - 0 \dots A_{3n}x_{n} \\ \vdots \\ b_{n} -A_{n1}x_{1} - A_{n2}x_{2} - A_{n3}x_{3}\dots 0 \end{bmatrix}=
$$

$$
\begin{bmatrix} \frac{1}{A_{11}}(b_{1}-A_{12}x_{2}-A_{13}x_{3}-\dots-A_{1n}x_{n}) \\
\frac{1}{A_{22}}(b_{2}-A_{21}x_{1}-A_{23}x_{3}-\dots-A_{2n}x_{n}) \\
\frac{1}{A_{33}}(b_{3}-A_{31}x_{1}-A_{32}x_{2}-\dots-A_{3n}x_{n})\\\vdots \\
\frac{1}{A_{nn}}(b_{n}-A_{n1}x_{1}-A_{n2}x_{2}-\dots-A_{nn-1}x_{n-1})\end{bmatrix}
$$

　上記より連立方程式で求めた形と同じになっていることが確認できます。

【ポイント：対角行列Dの逆行列】
　逆行列 (inverse matrix)とは行列Aに対して$${AA^{-1}=単位行列I}$$となる$${A^{-1}}$$を言います。上記の対角行列$${D}$$の逆行列$${D^{-1}}$$はすべての要素が逆数になります。

$$
\bm D=\begin{bmatrix} A_{11} & 0 & \ldots & 0 \\ 0 & A_{22} & \ldots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \ldots & A_{nn} \end{bmatrix}, \bm D^{-1}=\begin{bmatrix} \frac{1}{A_{11}} & 0 & \ldots & 0 \\ 0 & \frac{1}{A_{22}} & \ldots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \ldots & \frac{1}{A_{nn}} \end{bmatrix}
$$

４．PythonによるJacobi法の実装

　サンプル問題は下記の通りであり理論解は$${{x_{1}: 1, x_{2}: 1, x_{3}: -1}}$$です。

$$
2x_{1} + x_{2} + x_{3} =2\\
2x_{1} +3x_{2} + x_{3} =4\\
x_{1} + x_{2} +3x_{3} =-1
$$

　実装のポイントは下記の通りです。計算結果より147回のループで正しい近似解を得ることが出来ました。

行列をLDU分解して余剰行列R=(L+U)を作成できるようにした
解Xを求めるには最初に適当な初期値が必要なため乱数値で初期化
$${x_{n}->x_{n+1}}$$で更新していき残差が閾値以下になったらループを終了させる（無限ループにならないようにMAXループ数も設定）

[IN]
import numpy as np

class Jacobi:
    def __init__(self, A, b, thresh=1e-7, max_iter=1000):
        self.A = A
        self.b = b
        self.thresh = thresh
        self.max_iter = max_iter
        self.X0 = np.random.randn(len(b))
        
    def LDU_decomp(self, matrix):
        L = np.tril(matrix, -1) #下三角行列
        D = np.diag(np.diag(matrix)) #対角行列
        U = np.triu(matrix, 1) #上三角行列
        return L, D, U
    
    def solve(self):
        L, D, U = self.LDU_decomp(self.A) #L, D, Uを求める
        X = self.X0 #初期値
        for count in range(self.max_iter):
            X_next = np.linalg.inv(D).dot(self.b - (L+U)@(X)) #Jacobi法の計算式
            residual = np.sum(np.sqrt((X_next - X)**2))/np.sum(np.sqrt(X**2)) #残差
            X = X_next #更新
            count += 1
            if residual < self.thresh:
                break
        
        return X_next, count

np.random.seed(0)

A = np.array([[2, 1, 1],
                [2, 3, 1],
                [1, 1, 3]])

b = np.array([2, 4, -1])

jacobi = Jacobi(A, b)
jacobi.solve()

[OUT]
(array([ 0.99999995,  0.99999995, -1.00000004]), 147)

【結果の確認】
　出力を出しながらどういう風に変化するか確認してみました。Xの初期値は$${{x_{1.764}: 1, x_{2}: 0.4, x_{3}: 0.979}}$$で計算しており、数回程度では理論解$${{x_{1}: 1, x_{2}: 1, x_{3}: -1}}$$とは遠いところでジグザグ動いています。
　20回を超えたあたりから理論解に近い値に収束していっており、100回を超えるころにはほぼ近似解を取得できております。