
文系の blender 4.1 はじめての Geometry Node | 円を描く
文系のわれわれにとってジオメトリノードの数式ノードは鬼門です。
そこで、数式ノードに少しでも慣れるため、遠回りにごく普通の円(Circle)を描画してみます。それだけではつまらないので、ちょっとおもしろい円のアニメーションも制作します。
ジオメトリノードは英語での情報も多く、python との共通性もあるため、ここでは言語を英語としている。ただし訳語も可能なかぎり併記した。
環境 Blender 4.1.0 , Mac Mini M1 OS 14.2
そもそも Geometry Node とは?
ジオメトリノードは、ひとことでいえば、オリジナルのモディファイア。普段、ミラーモディファイアなどの便利な機能を使ってモデリングをしているが、加えて、自分独自のモディファイアを構築できるツールと考えてよいだろう。
準備
Curve > Nurbs Curve を追加する。(カーブ > NURBSカーブ)
Geometry Node
上部メニューの Geometry Nodes を選択
New(新規)ボタンをクリック
作成されたモディファイアを、HelloCircleとした(必須ではない)
円の作成
円は、もちろん通常は Curve Circle などを追加するだけで作成できるが、ここでは、三角関数を使い、円を作成してみる。
2次元の円の場合、円周の、X および Y 位置は、半径を 1 とすると、次のようになる。
X = sine(angle) Y = cosine(angle)
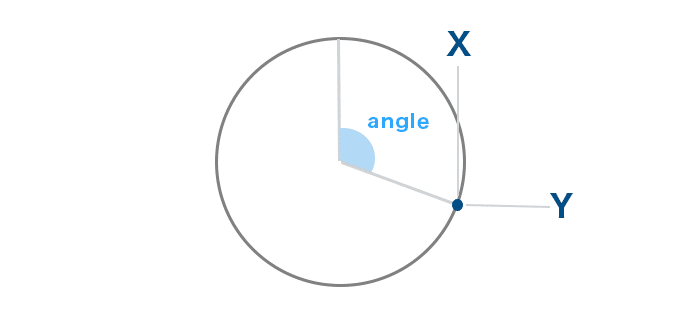
そこで、下で設定する各カーブポイントに、10, 20, 30 … のように角度(angle)を与えることにより、X, Y 座標を計算し配置することで円を描くことにする。
Nodeの作成
すでに設置されている Group Input(グループ入力) と Group Output(グループ出力)の間に以下のノードを組む。
Group Inputからは、追加したNurbs Curveの情報が出力されている。
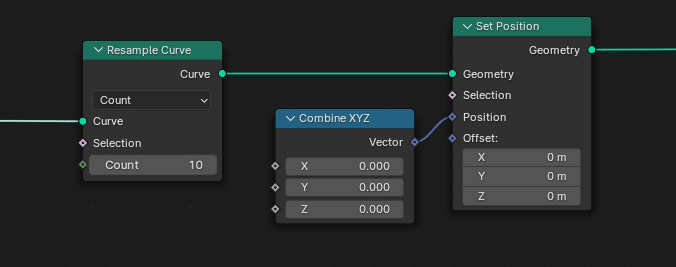
Resample Curve|カーブリサンプル
カーブの解像度設定と同じ。ここでは、カーブの制御点(カーブポイント)を10に細分化している。
Set Position |位置設定
上で作成したそれぞれのカーブポイントの位置を設定できる。
Combine XYZ |XYZ合成
X、Y、Z 軸のいずれか、あるいは複数の値をそれぞれ別個に受け取り、ベクトルにまとめることができる。まとめたベクトル情報は、Set Position の Position(位置)に渡す。
座標の計算
角度
まず、Index ノードを用いて、各カーブポイントに割り当てる角度(ラジアン)を用意する。
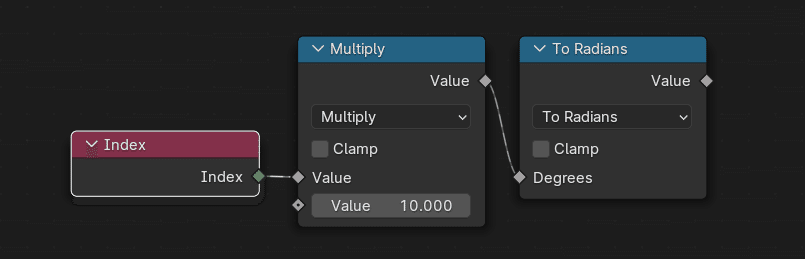
Index |インデックス
ここでは、各カーブポイントのインデックス番号、0 1 2 … 9 までの整数値が出力される。この値を角度として利用する。
Math - Multiply |数式 - 乗算
Mathノードのプルダウンで、Multiplyを選択。いわゆる掛算。ここでは、Index値を10倍し、0 10 20 30 … としている。
Math - To Radians |数式 - ラジアンへ
10, 20 などの度(angle)を、コンピュータが理解する単位、ラジアンへ変換する。
ラジアンは角度の単位のひとつで、1 度は、π÷180 radian
Sine, Cosine
上で出力されるラジアンの値を、Sine(サイン), Cosine(コサイン)ノードに渡し、それぞれ上述の Combine XYZノード、Y および X に入力する。
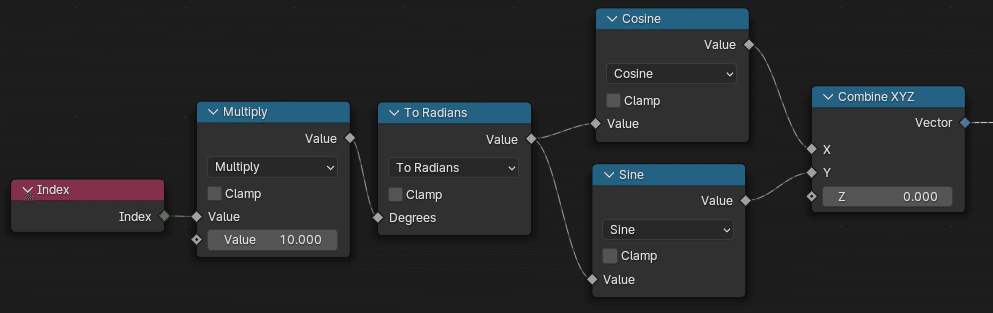
結果
90度分の 1 / 4 円が表示される。
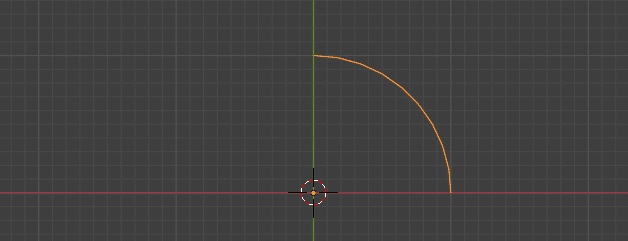
最初に作成した Resample Curve ノードの Count(数)を 37 に増やす。
無事、円が描画された。次は、このノードとテクスチャによる数値を用いて、すこし変化のある円を描いてみる。
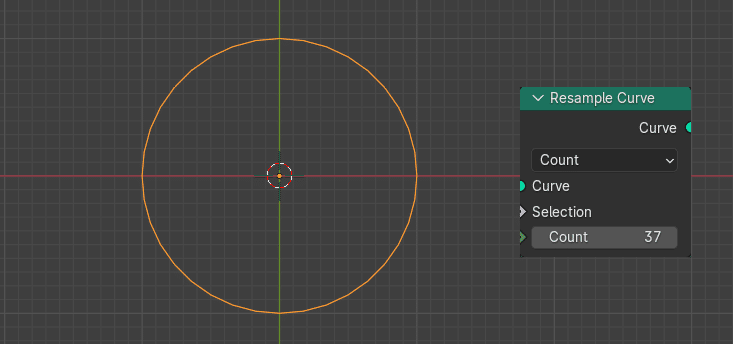
半径の変化
ここまでは半径が 1 のまま固定されているので、サイン、コサインからの出力に、Wave Texture(波テクスチャ) からの 0〜1 までの値を掛けてみる。半径が0〜1倍に大きく変化する。
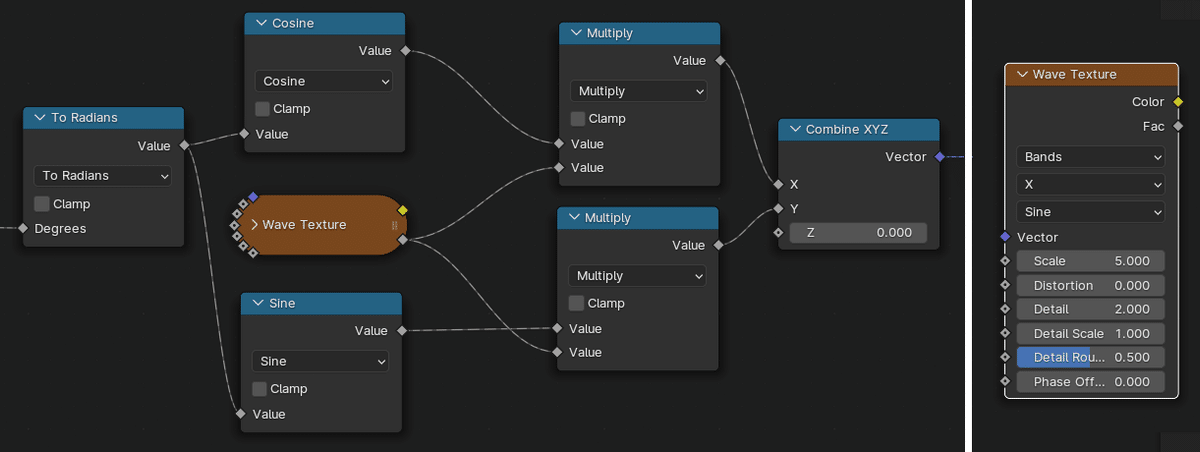
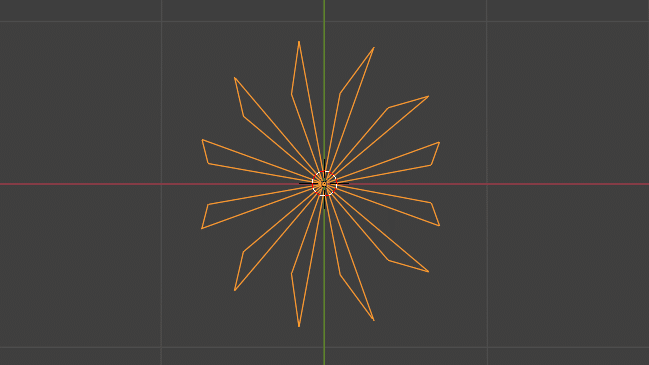
アニメーション
アニメーションを表示させる。
最初に作成した Resample Curve(カーブリサンプル)の Count(数) 項目に「#frame」と入力する。
適宜、フレーム数を、1000 などに増やす。
スペースバーを押し、アニメーションを開始する。
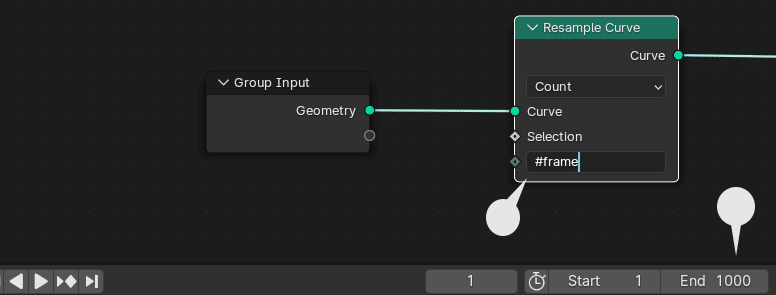
ノードの項目内に、#frame と入力することで、その項目をタイムラインに沿ってフレームごとに増やすことができる。
アニメーションを開始すると、異なる Count でさまざまなパターンが現れる。不思議。もちろん Wave Texture の設定値を変えたり、他の Texture に変更することで、また異なったパターンが現れる。

ノード全体
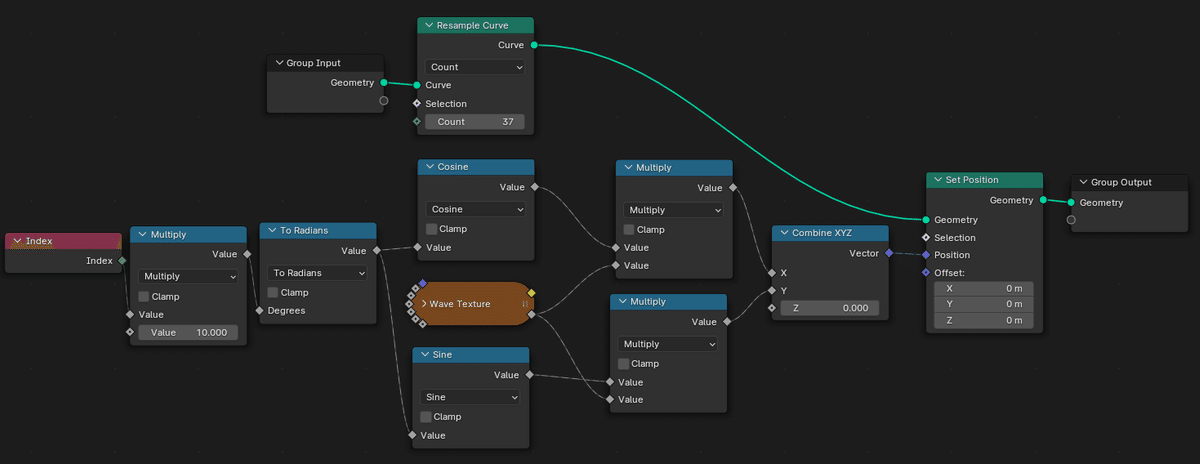
なお、ここまではあくまでカーブのままなのでレンダリングはされない。レンダリングするには一例として、下のように Set Position 以降のノードを組む。
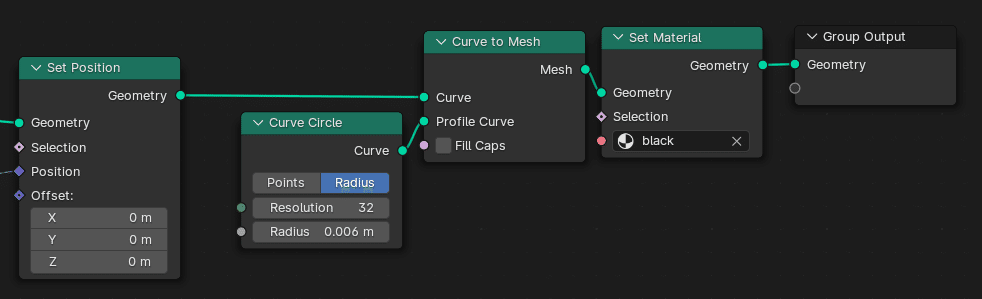
まとめ
ジオメトリノードでは紙などに書けば比較的かんたんな数式でもノードでつながなくてはならず、すこし煩雑なところがありますが、生成モデリングにはやはり数式ノードが欠かせません。
もちろんわたしには、なぜ上のようなパターンが生成されるのか正確にはわかりません。これは、マテリアルノードなどで、ノイズテクスチャを便利に利用していても、その関数の正確な内容については知らないのと同じです。
われわれ文系は、途中の過程はそのようにできているのだ、という鷹揚な理解に留め、なんとか結果のみを上手に利用できないかと、乏しい知恵を絞ります。
今回の図形はすこしヒトデや貝にも似ていますが、数式によるパターンがどこか自然界の現象や生物の形にも似ている、ということは昔から注目されており、その仕組みの解明はコンピュータの計算能力を待たなくてはならなかったのですが、初期の電子計算機の開発で有名なアラン・チューリングも興味があったようで、自ら「シマウマの縞をつくる方程式」を研究、開発し、今ではそのチューリングの式を使いシミューレーションで縞を再現できるとのことです。
