
【Python】Python初心者が、各年度のプロ野球選手成績を使って翌年のチームの順位・勝率予想をしてみた

はじめに
目標
各チームの
打席数が多い野手8人
投球回数が多い投手6人
最多セーブ投手
最多ホールド投手
の16人の成績を年度毎にまとめ、これを特徴量として
目的変数の翌年の順位を予想する。
また、FA移籍した選手のみ移籍後のチームの選手として扱う。
環境
OS:Windows11
ブラウザ:Chrome
コードを動かす環境:Google Colaboratory
データ格納先:Google SpreadSheet
データの参照元
選手の成績
プロ野球データFREAK
FA移籍データ・
Clickプロ野球
年度別チーム順位・勝率
Clickプロ野球
用意したデータの内容
年度別、チーム順位&勝率
FA移籍のデータ
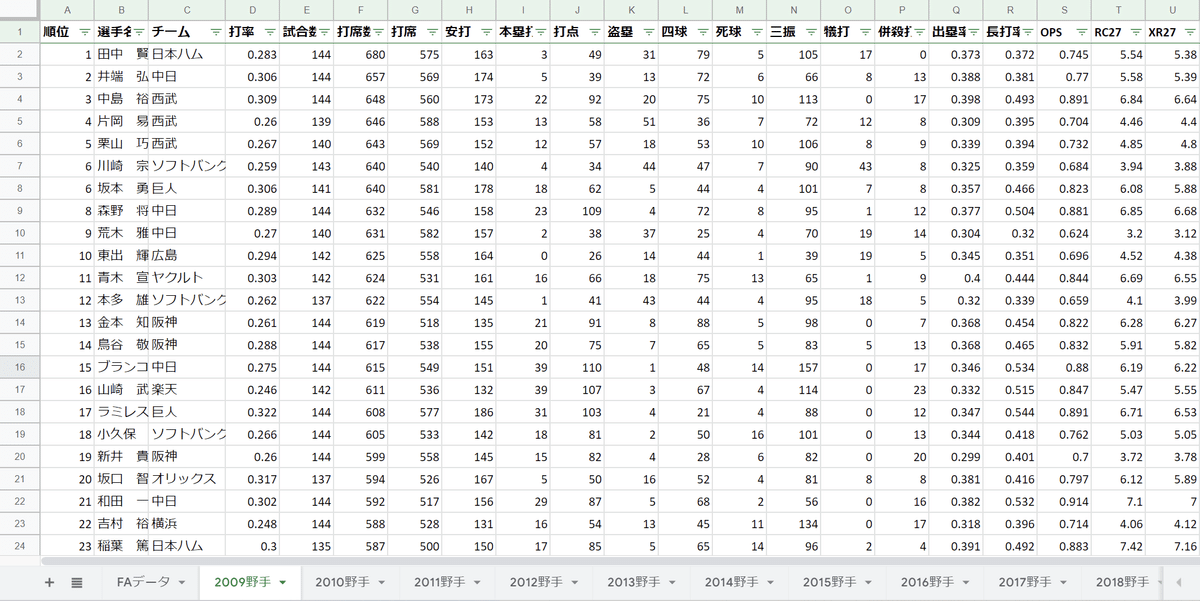
年度別打席が多い順の野手の成績
年度別投球回数が多い順の投手の成績
野手の成績と投手の成績はこんな感じ

Kerasを使ってディープラーニングさせてみる
データの前処理
まず、ColaboratoryでDriveのデータが使えるようにDriveにマウントする。
from google.colab import drive
drive.mount('/content/drive')野手の成績と投手の成績が入っているデータ(baseball.xlsm)から取得したい16人の成績データを年度毎チーム別に抽出して特徴量データX_dataに格納。
また、チーム順位をチーム順位が格納してあるデータから年度毎チーム別に抽出してy_dataに格納する。
filepath = '/content/drive/MyDrive/note/baseball.xlsm'
filepath2 = '/content/drive/MyDrive/note/rank.csv'
df = pd.read_excel(filepath,sheet_name =None)
df_rank = pd.read_csv(filepath2)
df_rank = df_rank.set_index('年度')
#不要データの削除
del df['FAデータ'], df['移籍']
print(type(df))
#チーム年度ごとに分けるためそれぞれリスト化
teams = ["巨人","阪神","横浜","広島","ヤクルト","中日","ソフトバンク","オリックス","西武","楽天","日本ハム","ロッテ"]
years = ["2009","2010","2011","2012","2013","2014","2015","2016","2017","2018","2019","2020","2021"]
X_data = []
y_data = []
#格納するデータのチームを指定する
for team in teams:
#格納するデータの年度を指定する
for year in years:
team_data = []
#エクセルファイルの全データをインポートしているので、タブ名:表データという辞書型で保存されているのでタブ名とデータごとに分ける
for df_name, year_df in df.items():
#指定した年度のデータのタブを抽出
if df_name[0:4] == year:
#野手のみを抽出
if df_name[len(df_name) - 2:] == "野手":
fielder_data = []
#指定したチームのデータのタブを抽出
f_team_df = year_df.query('チーム == @team')
f_team_df["year"] = int(df_name[0:4])
#打席数上位8名のデータを抽出して野手データに格納(格納されたデータ自体が打席数順のため並び変えしてない)
for i in range(0,8):
fielder_data.append(f_team_df.iloc[i].drop(["順位","選手名","チーム","year"]).to_list())
#野手データをチームデータに格納
team_data.append(fielder_data)
#投手のみを抽出
else:
pitcher_data = []
#指定したチームのデータのタブを抽出
p_team_df = year_df.query('チーム == @team')
p_team_df["year"] = int(df_name[0:4])
#投球回数上位6名のデータを抽出して投手データに格納(格納されたデータ自体が投球回順のため並び変えしてない)
for i in range(0,6):
pitcher_data.append(p_team_df.iloc[i].drop(["順位","選手名","チーム","year"]).to_list())
#セーブ数上位1名のデータを抽出して投手データに格納
p_team_df = p_team_df.sort_values('セーブ')
pitcher_data.append(p_team_df.iloc[0].drop(["順位","選手名","チーム","year"]).to_list())
#ホールド数上位1名のデータを抽出して投手データに格納
p_team_df = p_team_df.sort_values('ホールド')
pitcher_data.append(p_team_df.iloc[0].drop(["順位","選手名","チーム","year"]).to_list())
#投手データをチームデータに格納
team_data.append(pitcher_data)
#チームデータを特徴量用のX_dataに格納
X_data.append(team_data)
#チームデータを目的変数用のy_dataに格納
y_data.append(df_rank.at[int(year), team])
#train_test_splitで扱えるようにデータの型を変更
X_data = np.array(X_data)
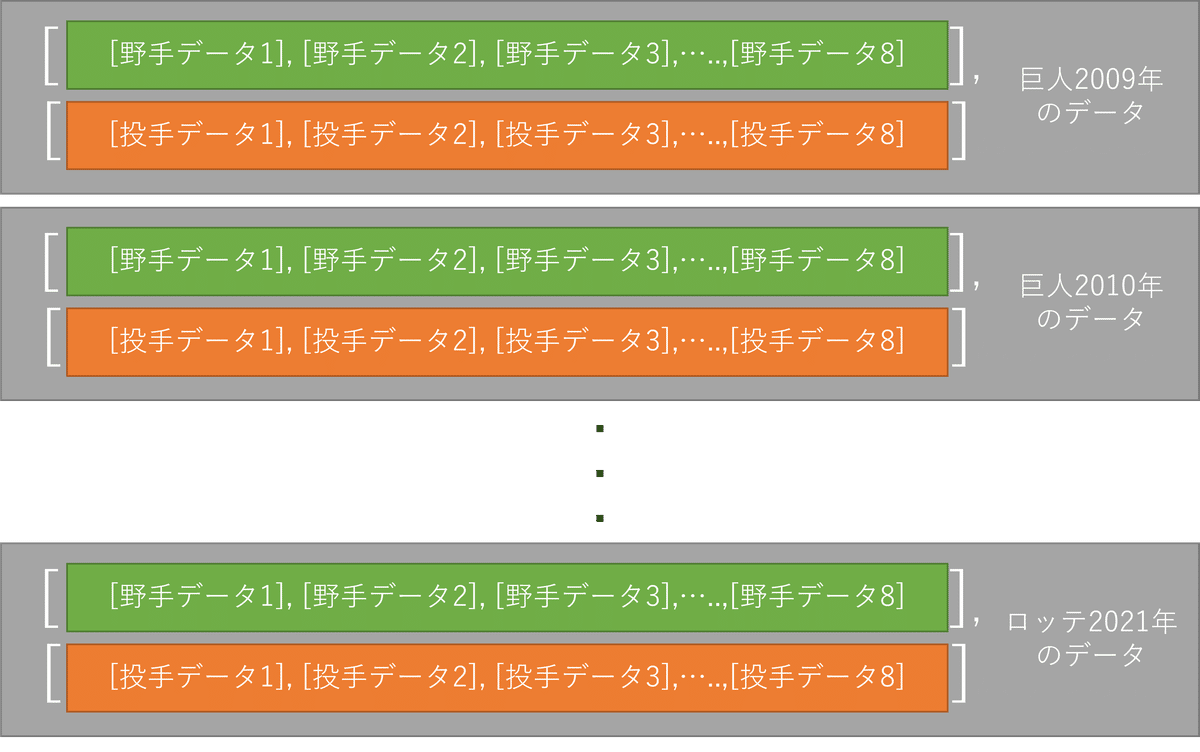
y_data = np.array(y_data)これでチーム毎、年度毎に以下のようなデータの形で抽出できた
[[2009巨人の全データ],
[2010巨人の全データ],
[2011巨人の全データ],
・
・
[2021ロッテの全データ]]
データの中身の詳細
学習させてみる
#train_test_splitで訓練データとテストデータに分ける
X_train, X_test, y_train, y_test = train_test_split(X_data, y_data,test_size=0.1, random_state=0)
#特徴量データを学習できる形に変換
shapes = X_train.shape[1] * X_train.shape[2] * X_train.shape[3]
X_train = X_train.reshape(X_train.shape[0], shapes)
X_test = X_test.reshape(X_test.shape[0], shapes)
model = Sequential()
# 4階層のモデルにする
model.add(Dense(128, input_dim=288, activation='relu'))
model.add(Dense(64, activation='relu'))
model.add(Dense(32, activation='relu'))
model.add(Dense(6, activation='softmax'))
# 損失関数にmse、最適化関数にadamを採用
model.compile(optimizer='adam', loss='mse', metrics=["accuracy"])
# モデルを学習させる
history = model.fit(X_train, y_train, epochs=32 , batch_size=1 , verbose=1, validation_data=(X_test, y_test) )データ数が少ないのでbatch_sizeは1
階層は4階層で試してみる
平方平均二乗誤差と結果
予測値を出力し、二乗誤差とepoch毎の予測値の正解データとの誤差を表示する
# 予測値を出力
y_pred = np.argmax(model.predict(X_test),axis = 1)
print(y_pred)
# 二乗誤差を出力
mse= mean_squared_error(y_test, y_pred)
print("REG RMSE : %.2f" % (mse** 0.5))
# epoch毎の予測値の正解データとの誤差を表示
plt.plot(history.history["accuracy"], label="acc", ls="-", marker="o")
plt.plot(history.history["val_accuracy"], label="val_acc", ls="-", marker="x")
plt.ylabel("accuracy")
plt.xlabel("epoch")
plt.legend(loc="best")
plt.show()
score = model.evaluate(X_test, y_test, verbose=0)
print("evaluate loss: {0[0]}\nevaluate acc: {0[1]}".format(score))結果がこちら
予想順位[5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5]
二乗誤差: 2.24
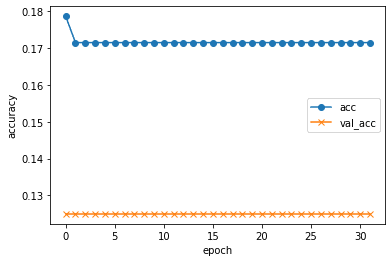
あれれ、まったく学習していない…
この後、いろんなハイパーパラメータをいじってみたが、学習する様子はなかったので、学習方法を変更することに…
線形回帰で予測をさせてみる
データ量が少なく特徴量が多いので、特徴量を順位に関係あるものだけに削り、データ量が少なくても扱いやすい線形回帰で予測を立ててみる
特徴量の相関関係を見てみる
特徴量が多すぎて学習のノイズになるものが多い可能性があるので順位との相関関係を野手データ、投手データでそれぞれ見てみる。(最初にやれって話だが)
先ほどの作ったデータセットの年度毎の各球団野手8人、投手8人のデータをそれぞれ平均して、順位(rank)との相関関係を出した結果が以下になる。


順位が6段階(1~6位)の表現しかなく、相関性を見るのに乏しいですが、
野手データだと
本塁打(home run)
打点(RBI)
四球(BB)
XR27
投手データだと
勝率(winning percentage)
失点(earned runs)
WHIP
に相関がありそうなことがわかる。(図が小さく見にくいですが)
選定した特徴量で線形回帰させる
上で出した相関がありそうな7つの特徴量を使って、線形回帰させてみる
#特徴量の抜き出し
data = pd.concat([f_data.loc[:,['home run','RBI','BB','XR27']], p_data.loc[:,['winning percentage','earned Runs','WHIP']]], axis=1).values
target = f_data.loc[:,'rank'].values
print(type(data))
#train_test_splitで訓練データとテストデータに分ける
X_train, X_test, y_train, y_test = train_test_split(data, target, random_state=0 ,test_size=0.2)
model = LinearRegression()
model.fit(X_train, y_train)
# 作成したモデルから予測(学習用、検証用モデル使用)
y_train_pred = model.predict(X_train)
y_test_pred = model.predict(X_test)平均二乗誤差と決定係数を算出する
# 平均二乗誤差:小さいほど誤差の小さなモデルと言える
print('MSE Train : %.3f, Test : %.3f' % (mean_squared_error(y_train, y_train_pred), mean_squared_error(y_test, y_test_pred)))
# 決定係数:回帰式の適合性の指標(1に近いほど良い)
print('R^2 Train : %.3f, Test : %.3f' % (model.score(X_train, y_train), model.score(X_test, y_test)))二乗誤差Train : 1.180, Test : 1.008
決定係数 Train : 0.600, Test : 0.617
決定係数が0.5以上あるのでそこそこの精度で出せたといえそう。
補足:一応、順位なので少数点以下を1~6位になるように丸めて平均二乗誤差と決定係数も出してみた
小数点以下を処理後のMSE Train : 1.234, Test : 0.969
小数点以下を処理後のR^2 Train : 0.600, Test : 0.617
そんなに変わらないのでやらなくてよかった
勝率予想をしてみる
目的変数の種類が「1,2,3,4,5,6」の6パターンしかなく連続した数字として予測することができずに、算出結果が1つ違うだけで大きく差が出てしまい、予測結果が少し荒くなってしまう
また、相関関係も見にくくわかりずらいので、0~1の連続した値をとる勝率で予想をしてみる
特徴量の相関関係を見てみる
先ほどと同様にの年度毎の各球団野手8人、投手8人のデータをそれぞれ平均して、今度は勝率(win_rate)との相関関係を出した結果が以下になる。


野手データだと
本塁打(home run)
打点(RBI)
XR27
投手データだと
勝率(winning percentage)
WHIP
に相関がありそうなことがわかる。
選定した特徴量で線形回帰させる
上で出した相関がありそうな5つの特徴量を使って、線形回帰で予測してみる
#特徴量の抜き出し
data = pd.concat([f_data.loc[:,['home run','RBI','XR27']], p_data.loc[:,['winning percentage','WHIP']]], axis=1).values
target = f_data.loc[:,'win_rate'].values
print(type(data))
#train_test_splitで訓練データとテストデータに分ける
X_train, X_test, y_train, y_test = train_test_split(data, target, random_state=0 ,test_size=0.2)
model = LinearRegression()
model.fit(X_train, y_train)
# 作成したモデルから予測(学習用、検証用モデル使用)
y_train_pred = model.predict(X_train)
y_test_pred = model.predict(X_test)平均二乗誤差と決定係数を算出する
# 平均二乗誤差:小さいほど誤差の小さなモデルと言える
print('MSE Train : %.3f, Test : %.3f' % (mean_squared_error(y_train, y_train_pred), mean_squared_error(y_test, y_test_pred)))
# 決定係数:回帰式の適合性の指標(1に近いほど良い)
print('R^2 Train : %.3f, Test : %.3f' % (model.score(X_train, y_train), model.score(X_test, y_test)))平均二乗誤差Train : 0.00115, Test : 0.00097
決定係数 Train : 0.754, Test : 0.794
となった。
今回は勝率なので1~0間の範囲ということがほぼ決まっているので平均二乗誤差は小さくなることが予測されたが、決定係数も順位予測から大分改善して学習の改善が見られた。
ついでに:特徴量を絞り目的変数を勝率にしてディープラーニングさせてみる
使う特徴量
野手データ
本塁打(home run)
XR27
投手データ
勝率(winning percentage)
WHIP
学習させてみる
#train_test_splitで訓練データとテストデータに分ける
X_train, X_test, y_train, y_test = train_test_split(X_data, y_data,test_size=0.2, random_state=0)
shapes = X_train.shape[1] * X_train.shape[2] * X_train.shape[3]
X_train = X_train.reshape(X_train.shape[0], shapes)
X_test = X_test.reshape(X_test.shape[0], shapes)
model = Sequential()
# ここにコードを記入してください(model.add)
#野手8人*特徴量2コ+投手8人*特徴量2コで32のinput_dimになる
model.add(Dense(64, input_dim=32, activation='relu'))
model.add(Dense(128, activation='relu'))
model.add(Dense(64, activation='relu'))
model.add(Dense(32, activation='relu'))
model.add(Dense(1))
# 損失関数にmse、最適化関数にadamを採用
model.compile(loss='mse', optimizer='adam',metrics='mae')
# モデルを学習させます
history = model.fit(X_train, y_train, epochs=32 , batch_size=3 , verbose=1, validation_data=(X_test, y_test) )特徴量を減らしたので32のinput_dimになり、勝率の計算になり分類ではなく回帰になるので出力層に活性化関数を用いない。
また、評価関数も[1,2,3,4,5,6]のような定数でないのでmeaで出す
epoch毎の誤差とスコア
# epoch毎の予測値の正解データとの誤差を表示
loss=history.history['loss']
val_loss=history.history['val_loss']
epochs=len(loss)
plt.plot(range(epochs), loss, marker = '.', label = 'loss')
plt.plot(range(epochs), val_loss, marker = '.', label = 'val_loss')
plt.legend(loc = 'best')
plt.grid()
plt.xlabel('epoch')
plt.ylabel('loss')
plt.show()
score = model.evaluate(X_test, y_test, verbose=0)
print("evaluate loss: {0[0]}\nevaluate mae: {0[1]}".format(score))
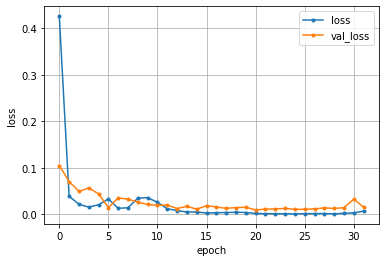
学習が収束していて、val_lassも大きな値が出ていないことから過学習も起きていなそうなことがわかる。
また、スコアも
mae: 0.09435509890317917
となり、線形回帰ほどではないが小さくなっているのがわかる
この記事が気に入ったらサポートをしてみませんか?
