
邪馬台国は見つかっていた【10】「秘密の距離」で萬二千余里の謎が解決する

ゆい:
「隠された秘密」って「徳川埋蔵金」的なやつ?
おじ:
説明いたしましょう!時は幕末、江戸幕府の御用金を秘密裏に・・・・・・じゃなくて、僕が説明したいのは古代の航海方法についてだよ。
ゆい:
航海方法?
おじ:
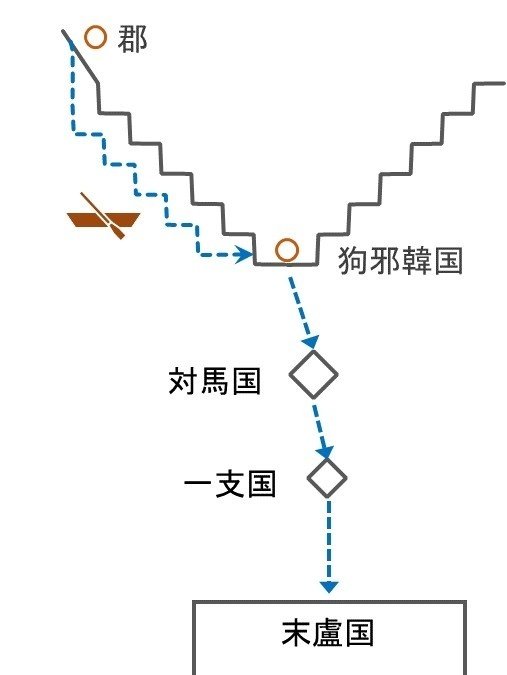
うん。帯方郡から狗邪韓国に向かう際の倭人伝の記述を見てみよう。
従郡至倭 循海岸水行 歴韓國 乍南乍東 到其北岸狗邪韓國 七千餘里
(帯方郡から倭の国へ行くには、海岸沿いに船を進め、韓国を通り南に行くかと思えば東に行き、又急に南へ行くというように向きを変え、その北岸の狗邪韓國へ行くまで七千里以上の距離がある)
おじ:
この説明でわかることは、当時の航海方法が「海岸沿い航法」だったということだ。古代の船は小さくて、動力も付いてない。当然、岸から離れると危険だし潮の影響も受けやすくなる。だから、なるべく海岸沿いに船を進める方法を取っていたんだ。
レン:
現代の船は大きくてエンジンも付いているから、岸から離れて航海する方が逆に安全だし燃料も節約できますね。
おじ:
そうだね。船の向きが急に南や東に変わったというのは、「海岸沿い航法」のなせる業だよ。
ゆい:
それが「秘密の距離」と関係あるの?
おじ:
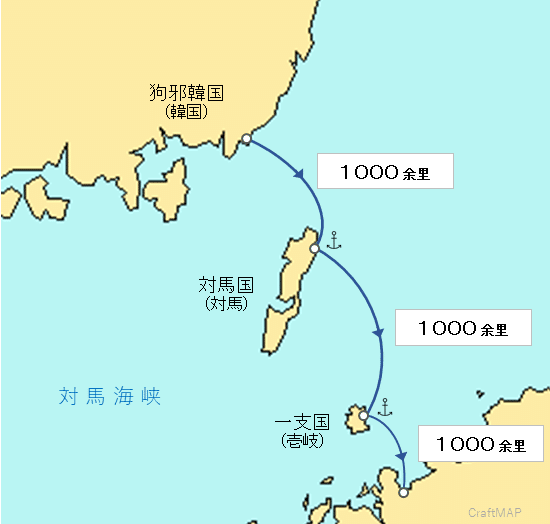
韓国から対馬海峡を渡る際、我々現代人は、次の図のように船が港から港へ直接進むと想像するだろう?
おじ:
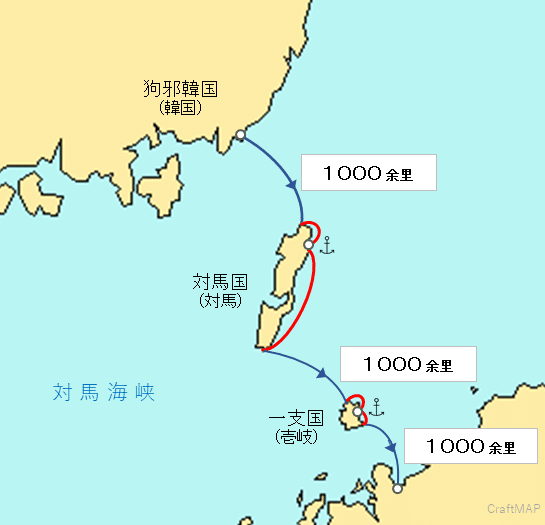
でも実際は次の図のような「海岸沿い航法」だった。
おじ:
この2つの図を比べて何か気が付かない?
ゆい:
「海岸沿い航法」の航行距離の方が長い……?
レン:
本当だ。赤線の岸づたいに進んだ距離の分、長くなっているんだ。魔法みたいに距離が増えた。
おじ:
正解!対馬と壱岐の海岸を航行した距離が「秘密の距離」の正体だよ。10700余里の中に、この距離は含まれていない。なぜなら「渡一海千餘里」の「一海」は島から島へと渡った距離だからね。つまり10700余里にこの海岸を航行した距離を足せばいいんだ。
レン:
対馬と壱岐の大きさは確か倭人伝に書いてあったぞ。対馬国は方可(縦横)400余里、一支国は方可300里だから……対馬国の海岸線は800余里、一支国の海岸線は600里、合計1400余里だ。10700余里に足すと……12100余里!

ゆい:
すごい!ニアピン賞じゃない?
おじ:
倭人伝の「萬二千餘里」に100里の差で合致している。まさにぴったりの数字だろう?
ゆい:
本当ね。

おじ:
「疑問1 倭人伝に書かれた距離を合わせても、萬二千餘里には1300里不足する」は対馬と壱岐の海岸航行距離を追加することで解決できた。埋蔵金ならぬ「埋蔵距離」が対馬海峡で見つかった、というわけさ。
ゆい:
「萬二千餘里の謎」はこれで解決ね。
この記事が参加している募集
この記事が気に入ったらサポートをしてみませんか?
