
図式で学ぶ量子論 #1 ~量子論の数学的構造~
連載の記事一覧:
#1 量子論の数学的構造
#2 CP写像の基礎
#3 確率論としての古典論・量子論(前編)
#4 確率論としての古典論・量子論(後編)
#5 プロセスの表現
番外編 2準位系から多準位系への演繹による拡張は難しい
番外編その2 堀田先生の書籍(中略)演繹的に導けていない
番外編その3 量子もつれ状態と非局所相関について
書籍「図式と操作的確率論による量子論」を22年10月に出版する予定です。本書の紹介を兼ねて,有限次元系の量子論の基礎を数回に分けて紹介したいと思います。
はじめに
量子論を理解するためには,その「数学的構造」と「操作的・確率的な性質」の両方を理解することが重要かと思います。操作的・確率的な性質のうち直観的に理解しやすいものから出発して,量子論の数学的構造や他の性質を素直に導ければ都合がよいのですが,今のところ容易に導く方法は知られていないようです。結局,量子論を理解するためには,まず数学的構造を理解することが近道だと思います。
この連載では,はじめに量子論の数学的構造の全体像をできるだけ整った形で説明することを試みます。次に,その構造を用いて量子論の操作的・確率的な性質を論じます。これにより,できるだけ素直に量子論の基礎を理解してもらうことをめざします。
連載「図式で学ぶ線形代数」で述べた線形代数の基礎や図式を前提知識として用います。これらの知識があまりなくてもある程度はわかると思いますが,必要に応じて参照してください。
準備

はじめに,この資料の立場を整理しておきます。物理的な概念にはほとんど基づかないことがこの資料の特徴です。
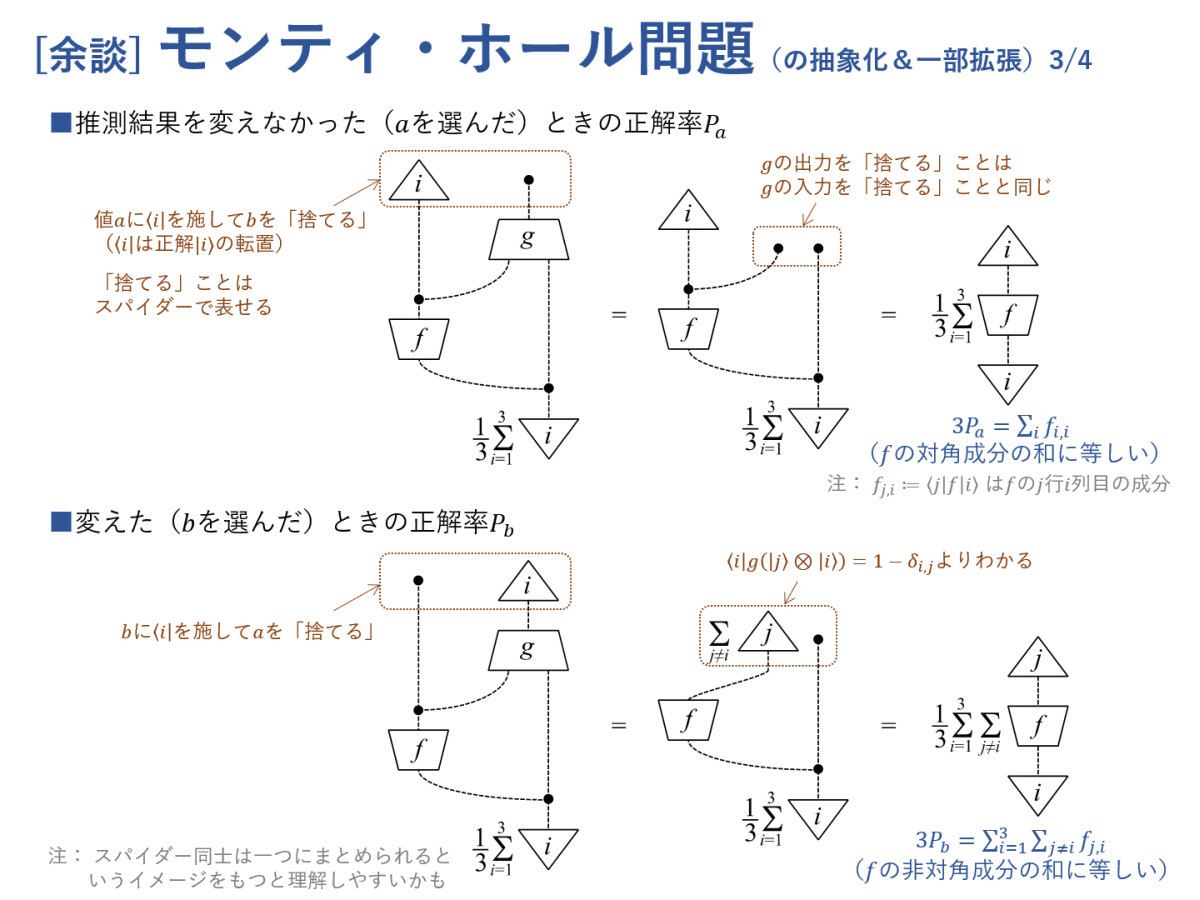
量子論の数学的構造の話に移る前に,古典論(=古典確率論)や量子論の図式についてイメージをつかんでもらうために一つ例を挙げておきます。この例は,モンティ・ホール問題とよばれる古典論に関する有名な問題です。やや複雑な問題なのですが,図式を使えば比較的素直に定式化できます。古典論と量子論の図式は結構似ていますので,この例を通して図式の便利さや面白さが何となく伝われば幸いです。



操作論の規則
では,量子論の数学的構造の話をしたいと思います。準備として,古典論や量子論を含むより汎用性が高い理論である,操作論について説明します。後で,操作論の特別な場合として古典論や量子論を定めます。
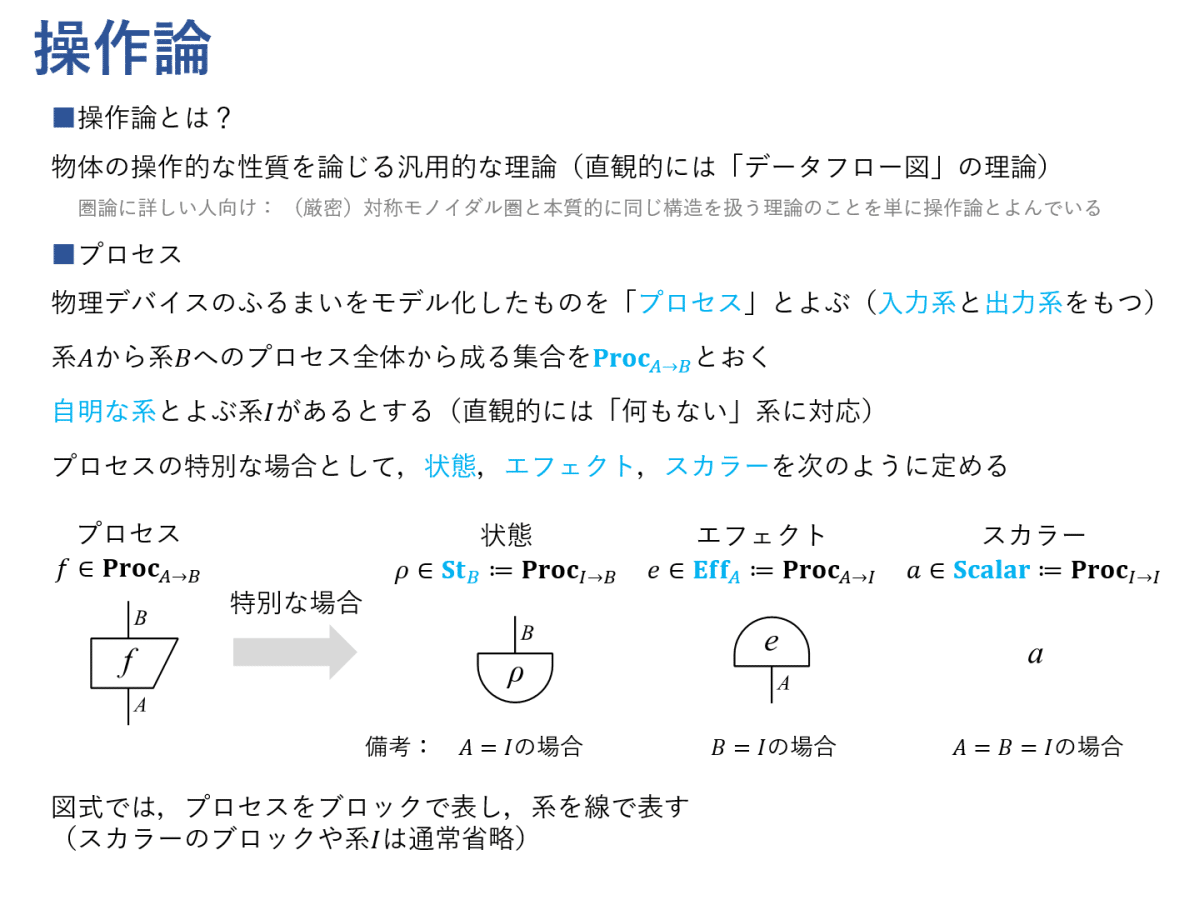
上のスライドでは,いくつかの用語を定めています。
次に,操作論の規則をすべて示します。操作論の図を「データフロー図」のように捉え,何らかの情報が系(線)に沿って下から上に流れるようなイメージをもつと,理解しやすいのではないかと思います。
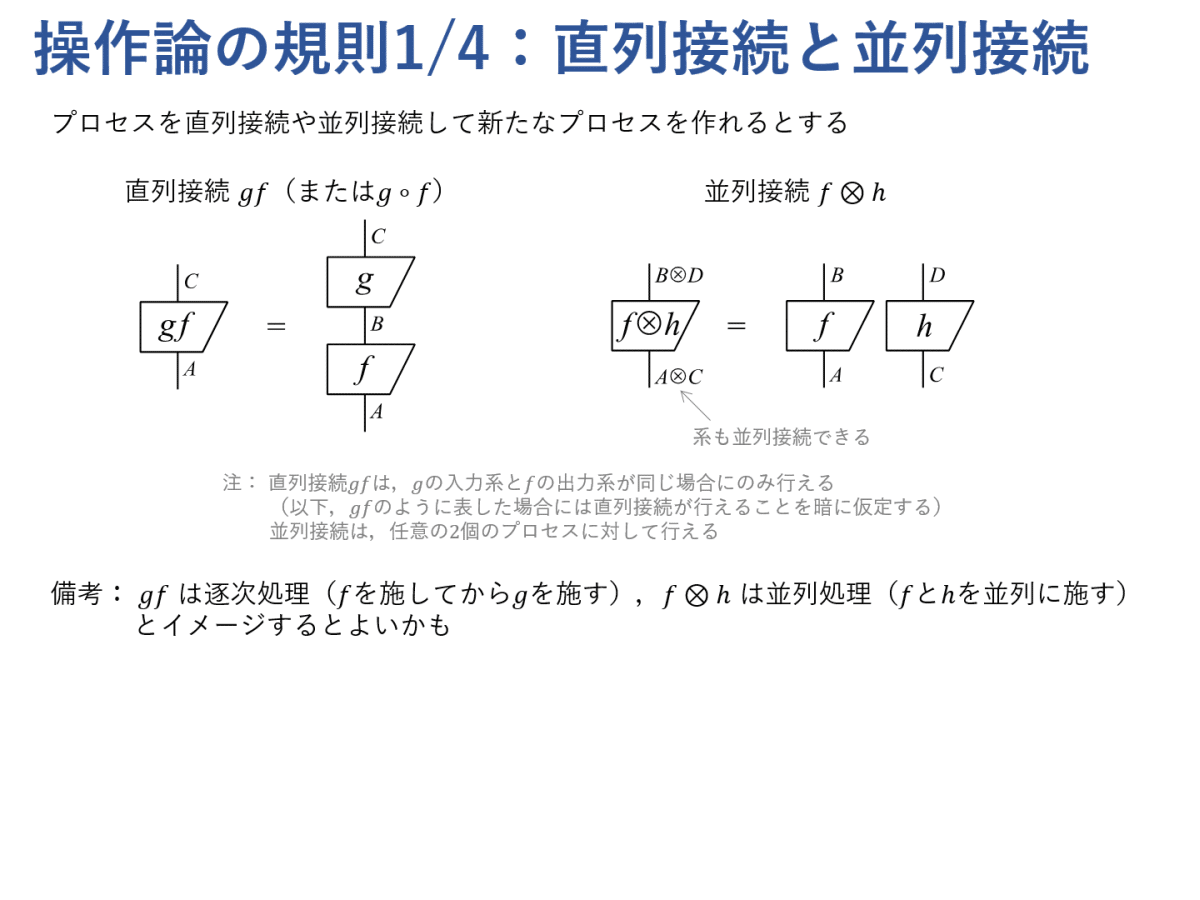
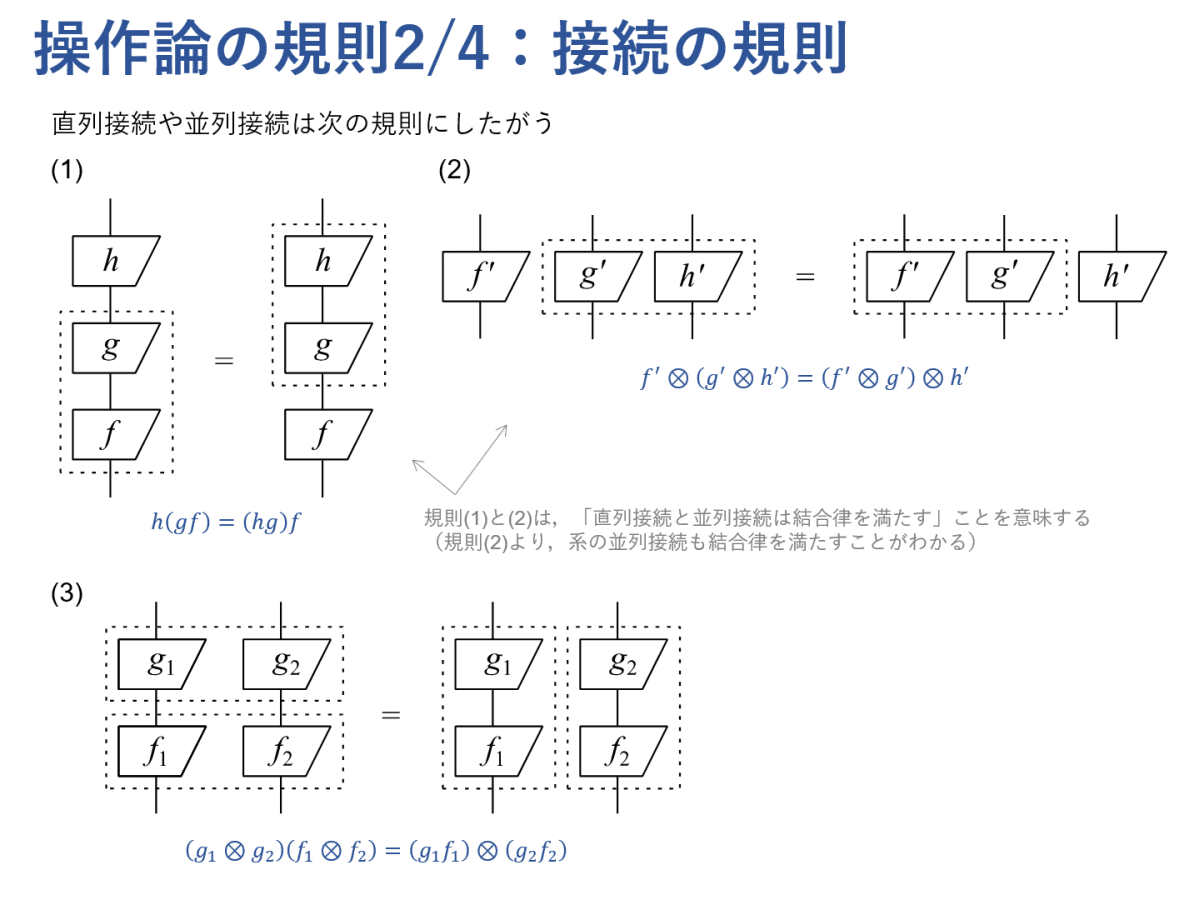

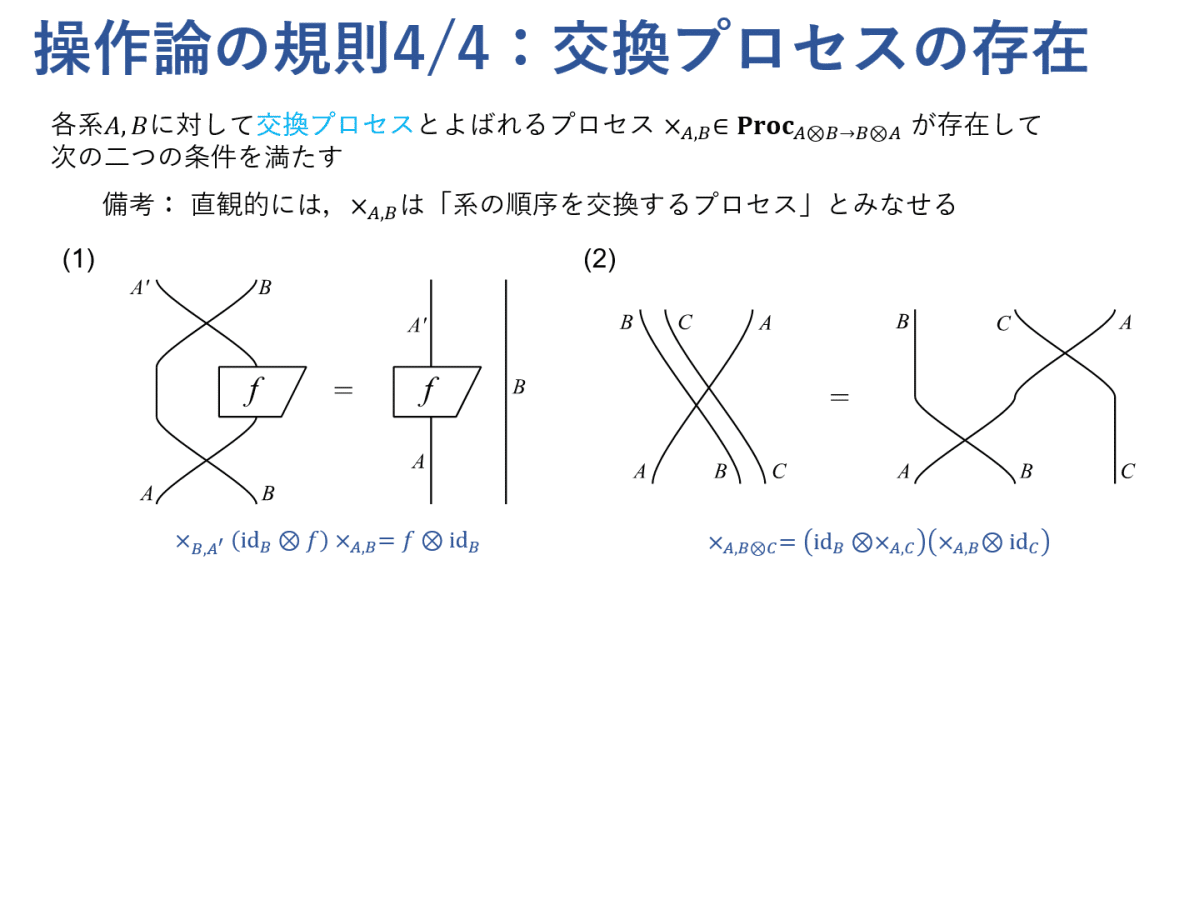
大ざっぱに述べると,操作論とは直列接続と並列接続ができるようなプロセスに関する理論です。ただし,これらの接続はいくつかの基本的な規則を満たしており,さらに恒等プロセスと交換プロセスが存在している必要があります。
これらの規則さえ満たしていれば操作論として扱えます。これらの規則からいくつかの基本的な性質を導けるのですが,その詳細は本書を参照してください。
次は余談です。操作論は,数学的には圏論における「厳密対称モノイダル圏」の理論といえます(難しい名前が付いていますが,すでに述べたように定義は簡単です)。参考までに「圏」の定義について紹介しておきます。

なお,ここでは余談として圏論の話をしましたが,この連載では圏論の知識は不要です。今後は,圏論の話はほぼしない予定です。
操作論の例
操作論について具体的なイメージをつかんでもらうために,いくつかの例を紹介します。

操作論の代表例の一つは線形代数です。線形代数と操作論の対応関係を示します。行列が操作論のプロセスに対応し,ヒルベルト空間(またはベクトル空間)が系に対応することが何となくわかると思います。
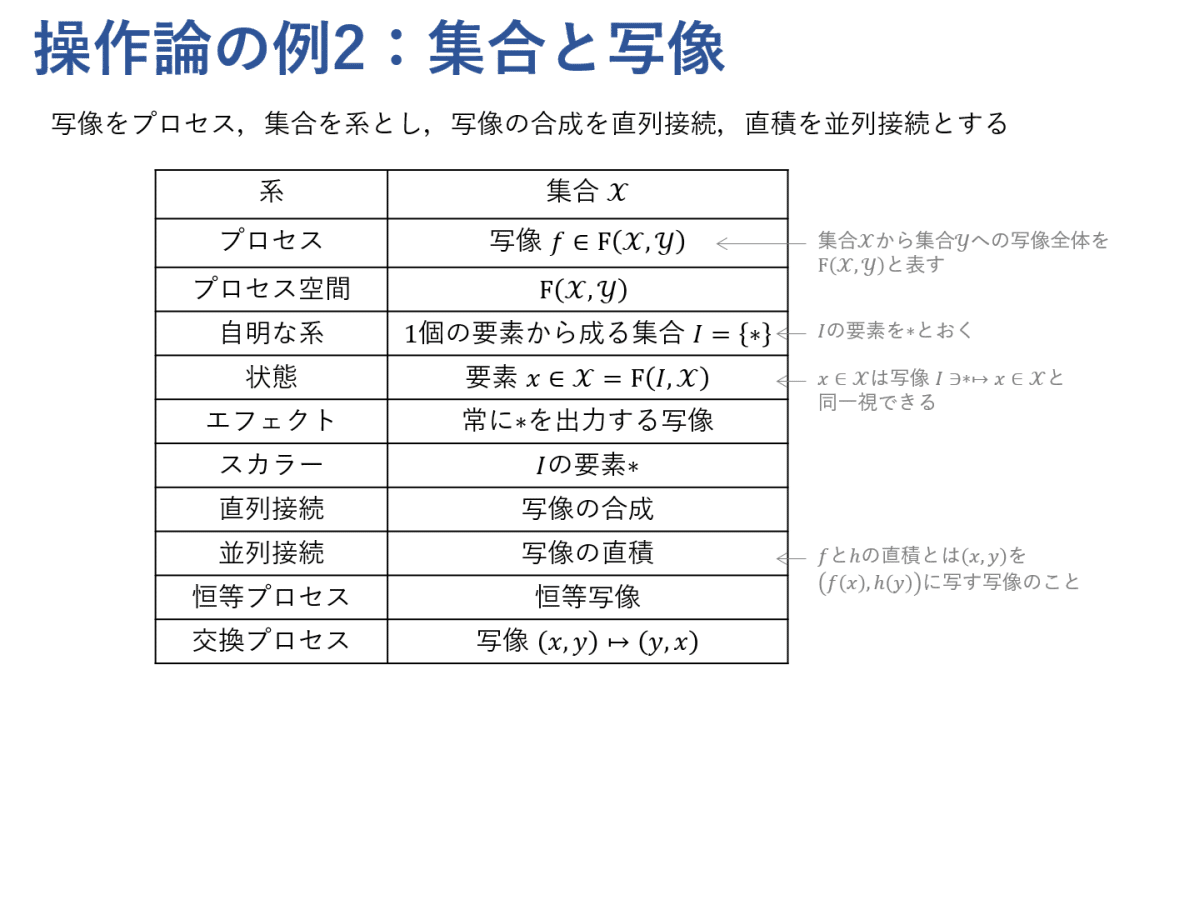
線形写像に限らない任意の写像をプロセスとするような操作論も考えられます。この場合,集合が系になります。並列接続は,テンソル積ではなく直積に対応します。

プログラムや作業手順,料理のレシピなども操作論とみなせます。直列接続は逐次的に施すことに対応し,並列接続は並列に施すことに対応します。古典論や量子論の操作的な性質を考えるときは,この例をイメージするとわかりやすいかもしれません。

最後の例は,可換群を系とする操作論です。ベクトル空間ではスカラー倍と和が定義されていますが,和のみが定義された集合を可換群とよびます。このように,直観的には和という演算さえあれば操作論を作れます。ベクトル空間は可換群の特別な場合とみなせますので,この操作論を拡張したものが線形代数の操作論といえます。なお,線形代数のテンソル積を可換群のテンソル積として理解すると,テンソル積の理解が深まるかもしれません。
古典論と量子論
古典論と量子論は,特別な性質を満たす操作論として定められます。

古典論の数学的構造は,二つの公理を満たす操作論として定められます。

先ほど示した公理から,上で示した表が得られます。

古典論の確率的な性質との対応についてイメージをつかんでもらうために,例を挙げています。大ざっぱに述べると,状態とは確率分布のようなもので,プロセスとは確率分布を確率分布に写す写像のようなものといえます。

有限次元系の量子論の数学的構造も,二つの公理を満たす操作論として定められます。また,これらの公理は古典論の場合と似ています。量子論(量子情報理論)の基礎をひととおり理解するためには,この構造を理解することが重要だと思います。
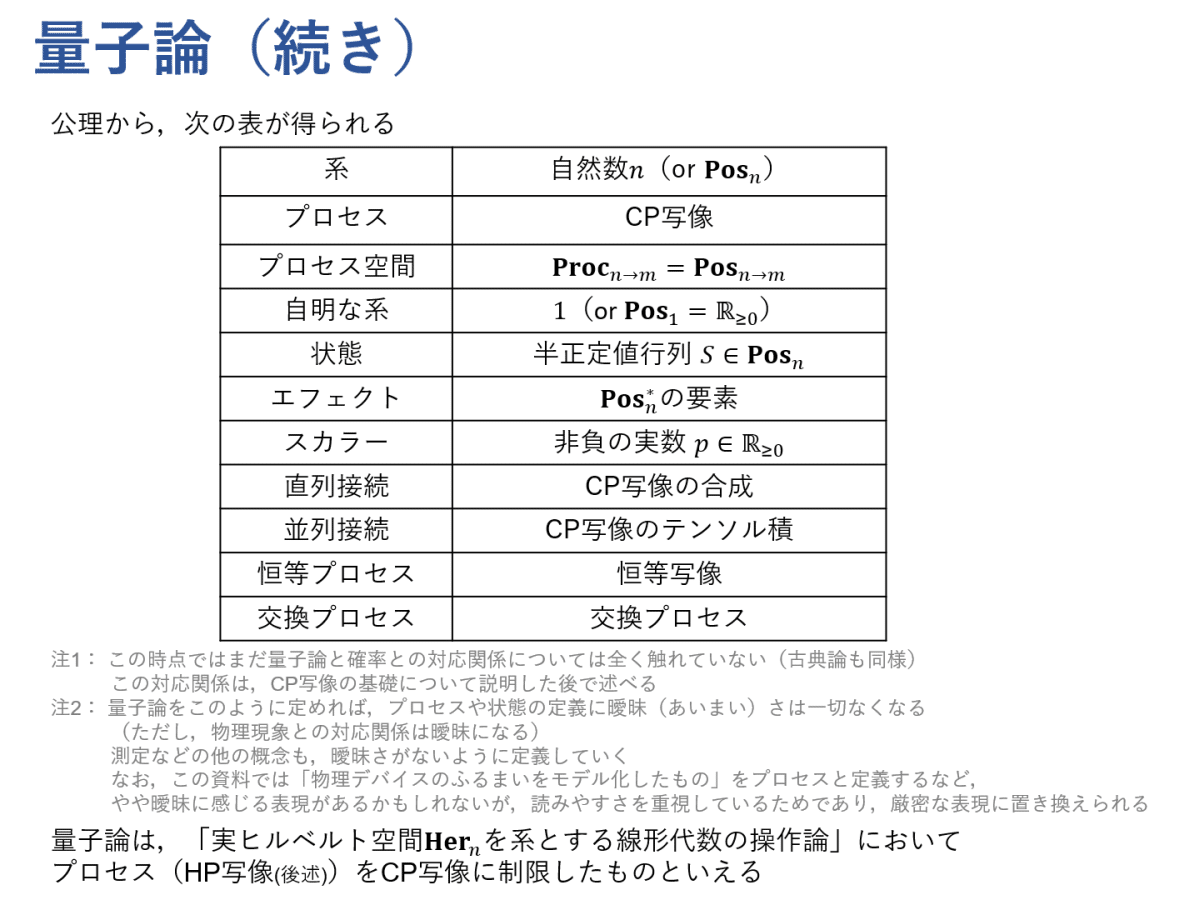
古典論の場合と同様に,上で示した表が公理から得られます。

量子論と確率論との大まかな対応関係を示します。ここでは一連のプロセスを操作論の図式として表現していますが,これから説明するCP写像の図式表現を理解すれば各プロセスの具体的なふるまいなども図式で表現&計算できるようになります。
古典論の数学的構造は確率分布というイメージから直観的に理解しやすいと思いますが,量子論の数学的構造を直観的に理解することは困難です。冒頭でも述べたように,量子論の状態やプロセスがなぜ半正定値行列やCP写像になるかについてを素直に理解する方法はまだ知られていないようです。ただし,この構造をいったん受け入れてしまえば,これから述べる操作的・確率的な性質の多くは直観的に理解できるようになると思います。
最後に,余談として,想定される主な質問に対して答えてみました。

今回は,量子論の数学的構造を説明しました。大ざっぱには,量子論はCP写像をプロセスとする操作論といえます。このため,量子論を理解するためにはCP写像を十分に理解することが重要です。
次回では,CP写像について説明します。また,次々回以降では,量子論と確率論との対応関係について述べながら,量子論の操作的・確率的な性質を中心に説明する予定です。
この記事が気に入ったらサポートをしてみませんか?
