第5章 戦略評価編 第5節ケリー基準(ベッティング法)

今回もstefan jansen読んでいきましょう！
この内容は中々面白いと思います。株式市場にケリー基準を応用するという話ですからね(*'ω'*)

ケリー基準とは

ケリー基準はギャンブルで長い歴史を持っています。なぜなら、期末の財産額を最大化するために、さまざまな（しかし好ましい）オッズで（無限の）賭けのそれぞれにどれだけ賭けるかについてのやり方を教えてくれるからです。ベル研究所のクロード・シャノンの同僚であったジョン・ケリーによって1956年に情報レートの新しい解釈として出版されました。彼は新しいクイズ番組「64,000ドルの質問」で候補者にかけられた賭けに興味をそそられました。西海岸の視聴者が3時間の遅延を利用して、受賞者に関するインサイダー情報を取得しました。

ケリーは、オッズが良好であるが不確実性が残っている場合、長期的な資本成長に最適な賭けを解決するためにシャノンの情報理論へのつながりを引き出しました。彼のルールは、各ゲームの成功のオッズの関数として対数資産を最大化します。資産の一定比率を賭けるので、全財産飛ぶことは理論上そもそもありえません。

公式

ケリーは、バイナリの勝敗のゲームを分析することから始めました。主な変数は次のとおりです。

b：オッズは、1ドルの賭けに勝った金額を定義します。オッズ= 5/1は、賭けが勝った場合に5ドルの利益に加えて、1ドルの資本の回復を意味します。
p：確率は、好ましい結果の可能性を定義します。
f：現在の資本に対する賭け金の割合。
V：賭けの結果としての資本の価値。

ケリーのルールは、無限に繰り返される賭けの価値の成長率Gを最大化することを目的としています。

インポートと設定

import warnings
warnings.filterwarnings('ignore')

%matplotlib inline
from pathlib import Path

import numpy as np
from numpy.linalg import inv
from numpy.random import dirichlet
import pandas as pd

from sympy import symbols, solve, log, diff
from scipy.optimize import minimize_scalar, newton, minimize
from scipy.integrate import quad
from scipy.stats import norm

import matplotlib.pyplot as plt
import seaborn as sns

sns.set_style('whitegrid')
np.random.seed(42)

DATA_STORE = Path('..', 'data', 'assets.h5')

最適解を求める

sympyのライブラリを使用して、公式を解きたいと思います。

share, odds, probability = symbols('share odds probability')
Value = probability * log(1 + odds * share) + (1 - probability) * log(1 - share)
solve(diff(Value, share), share)

出力

[(odds*probability + probability - 1)/odds]

f, p = symbols('f p')
y = p * log(1 + f) + (1 - p) * log(1 - f)
solve(diff(y, f), f)

出力

[2*p - 1]

これで最適解を得ることが出来ました。

S&P500のデータを取得

with pd.HDFStore(DATA_STORE) as store:
   sp500 = store['sp500/stooq'].close

データの期間は1950年1月3日～2019年12月31日までのデイリーの終値データになります。

平均と標準偏差を計算

今回は25年移動平均と標準偏差を計算してから、平均値-2σ、平均値、平均値+2σをプロットします。

annual_returns = sp500.resample('A').last().pct_change().dropna().to_frame('sp500')

return_params = annual_returns.sp500.rolling(25).agg(['mean', 'std']).dropna()

return_ci = (return_params[['mean']]
               .assign(lower=return_params['mean'].sub(return_params['std'].mul(2)))
               .assign(upper=return_params['mean'].add(return_params['std'].mul(2))))

return_ci.plot(lw=2, figsize=(14, 8))
plt.tight_layout()
sns.despine();

単一アセットのケリー基準ーインデックスリターン

金融市場の状況では、結果と代替案はどちらもとても複雑ですが、ケリールールロジックはそれでも使えます。これは、エドソープによって有名になりました。エドソープは最初にケリー基準をギャンブルに応用し、後にヘッジファンドのプリンストン/ニューポートパートナーズでも運用に成功しました（「ディーラーをやっつけろ」引用）

株やギャンブルの絶え間ない結果により、資本の成長率は、数値的に最適化できるさまざまな収益の確率分布の統合によって定義されます。 scipy.optimizeモジュールを使用して、最適なf *(オプティマルfと呼ぶ)についてこの式を解くことができます：
※掛け金の比率は0~200%に設定しております。

def norm_integral(f, mean, std):
   val, er = quad(lambda s: np.log(1 + f * s) * norm.pdf(s, mean, std), 
                              mean - 3 * std, 
                              mean + 3 * std)
   return -val

def norm_dev_integral(f, mean, std):
   val, er = quad(lambda s: (s / (1 + f * s)) * norm.pdf(s, mean, std), m-3*std, mean+3*std)
   return val

def get_kelly_share(data):
   solution = minimize_scalar(norm_integral, 
                       args=(data['mean'], data['std']), 
                       bounds=[0, 2], 
                       method='bounded') 
   return solution.x

annual_returns['f'] = return_params.apply(get_kelly_share, axis=1)

return_params.plot(subplots=True, lw=2, figsize=(14, 8));

パフォーマンス評価

(annual_returns[['sp500']]
.assign(kelly=annual_returns.sp500.mul(annual_returns.f.shift()))
.dropna()
.loc['1900':]
.add(1)
.cumprod()
.sub(1)
.plot(lw=2));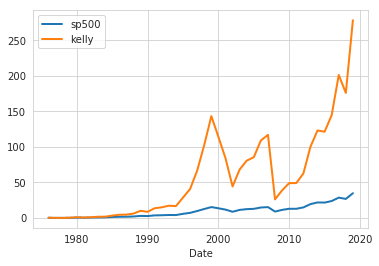

ケリー分数の計算

m = .058
s = .216

# Option 1: minimize the expectation integral
sol = minimize_scalar(norm_integral, args=(m, s), bounds=[0., 2.], method='bounded')
print('Optimal Kelly fraction: {:.4f}'.format(sol.x))

出力結果

Optimal Kelly fraction: 1.1974

多資産のケリー基準

ここでは、さまざまな株式の例を使用します。 E. Chan（2008）は、ケリールールのマルチアセットへの応用方法について示しており、その結果は平均分散最適化からの（潜在的に活用されている）最大シャープ比ポートフォリオに相当します。

計算には、共分散行列の逆である精度行列と戻り行列の内積が含まれます。

データから取得しますが、今回用いるデータはS&P500の構成銘柄のうち482銘柄で期間は1962年1月2日～2018年3月27日までのデイリーのデータになります。with pd.HDFStore(DATA_STORE) as store:

   sp500_stocks = store['sp500/stocks'].index 
   prices = store['quandl/wiki/prices'].adj_close.unstack('ticker').filter(sp500_stocks)

monthly_returns = prices.loc['1988':'2017'].resample('M').last().pct_change().dropna(how='all').dropna(axis=1)
stocks = monthly_returns.columns
monthly_returns.info()

精度行列の計算

cov = monthly_returns.cov()
precision_matrix = pd.DataFrame(inv(cov), index=stocks, columns=stocks)

kelly_allocation = monthly_returns.mean().dot(precision_matrix)

kelly_allocation.sum()

ポートフォリオの中の最も大きなアロケーション

kelly_allocation[kelly_allocation.abs()>5].sort_values(ascending=False).plot.barh(figsize=(8, 10))
plt.yticks(fontsize=12)
sns.despine()
plt.tight_layout();

ポートフォリオ vs S&P500

ax = monthly_returns.loc['2010':].mul(kelly_allocation.div(kelly_allocation.sum())).sum(1).to_frame('Kelly').add(1).cumprod().sub(1).plot(figsize=(14,4));
sp500.filter(monthly_returns.loc['2010':].index).pct_change().add(1).cumprod().sub(1).to_frame('SP500').plot(ax=ax, legend=True)
plt.tight_layout()
sns.despine();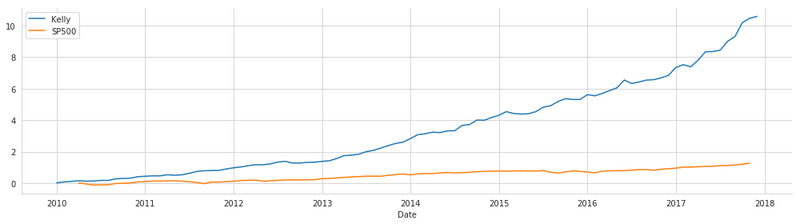

まとめ

ケリー基準の株式市場への応用方法をご存じない方々のために参考になればと思います(*'ω'*)

​