グリーン関数の定義"ΔG=δ"とはどういう意味か？ 数学的に正しい意味を知る

グリーン関数との出会いと困惑

　理学部の1・2年のカリキュラムにおいて楽しみだったのは電磁気学の講義である。私は物理学科ではないが、地球物理において重要な基礎の物理の中核であること、そして、電磁気学は数学の中でもっとも好きな分野であったベクトル解析を生み出し、また電磁気学自体がベクトル解析の最初の応用となることから、物理学科の電磁気学のコースを概ね履修した。

　電磁気学のなかで困惑したのが、真空中に連続的に分布する（静止した）電荷によって生じる静電場を、「グリーン関数」なるものを使って求める項目である。電場Eのスカラーポテンシャル、すなわちE=-∇φとなるスカラー関数φに対して、マクスウェル方程式から微分方程式∆φ=σ/ε_0を導くのは難しいことではない。ここで、σは電荷の密度、ε_0は真空中の誘電率である。さて、この微分方程式を解けば、スカラーポテンシャルφがわかり、そこから電場Eを求めることができる。この微分方程式の解き方は、多くの講義や教科書で次のように解説される。

1.グリーン関数Gを求める。すなわち、∆G(x)=δ(x)となるような関数Gを求める。たとえば空間が単純に3次元ユークリッド空間ならG(x)=-(4π|x|)^(-1)である。（なお、教科書によっては、∆G(x)=-δ(x)としていることもあるが、∆は線形性をもつので結果が-1倍になるだけである）

2.上で求めたグリーン関数Gを用いて、微分方程式の右辺σ/ε_0を畳み込み積分したものが解である。すなわち、φ(x) =∫ G(x-x')σ(x')/ε_0 dx' である。

　この解法は物理的には意味が分かりやすい。デルタ関数δ(x)は「原点だけに分布する単位量のソース(源)」の意味である。よって、「∆G(x)=δ(x)」の解G(x)は、原点だけにポツンとソースがあるとき、そこから出ている場を様子を記述する。連続的に分布する電荷σを、1点だけの電荷ソースの集まりだと思えば、それら1つ1つのソースから出るスカラーポテンシャルの場の重ね合わせが、求めたい全体のスカラーポテンシャルφである。そしてそれは、重ね合わせの積分によって表現される。数式と物理的意味が見事に対応していて美しい解法であるように思える。

　しかし、よく考えると、「∆G(x)=δ(x)」とはどういう意味であるか？ この式はGに対する偏微分方程式であるが、右辺はデルタ関数であり、これは通常の関数ではない。「超関数」と呼ばれるものである。

　おそらく、古典的な電磁気学を履修したり独学したりした人のなかには、このような数学的な厳密さがどこか引っ掛かっていまいち飲み込めていない人が一定の割合でいるのではないか。私もかつてそうであったので、同じような人がいたときにこの記事が少しでも参考になればいいと思っている。

超関数とは？

　超関数という言葉は、名前だけはよく知られているがそれが一体何を意味するのかはあまり知られていない。この記事でも、正確な定義を述べることはしないが、超関数とは

①性格の良い関数(具体的には、コンパクトな台を持つ=ある有界閉集合を除いて0であるC^∞級関数)のベクトル空間Fから実数体or複素数体Kへの線形写像であり、

②ある意味で連続性を持つもの

である。注意したいことは、超関数は通常の関数とは異なり、数から数への写像ではない点である。具体的にデルタ関数δで説明する。

　まず、デルタ関数δの定義は、次の通りである。性格の良い関数のベクトル空間Fの元fに対して、δを作用させた値<δ,f>を<δ,f>=f(0)で定義する。この記事を最後まで読めばわかるように、<δ,f>とは、「気持ち」としては∫δ(x)f(x)dxを表している。よく「デルタ関数の性質」として物理の本に書かれている「∫δ(x)f(x)dx = f(0)」とは、実は性質というよりもむしろこの定義のことである。このように定義すれば、δはFからKへの線形写像になる。しかも、ある意味で連続性が成立する写像なのである。このような線形写像のことをデルタ関数という。なお、積分の区間は特に指摘しない限り、考えている領域全体である。デルタ関数を扱う事情があるので、領域は原点0を含んでいるものとする。（最後の2文は細かいことなので気にしすぎることはないです）

　よくデルタ関数を無理矢理「普通の関数」として表現するために、「δ(x)=0 (x≠0), δ(0)=∞」と書いている記述が見られるが、これは極めて不正確である。実際、∫δ(x)f(x)dx = f(0)が全てのf∈Fで成立するような可積分関数δは存在しないことが知られている。ゆえに、デルタ関数を「普通の関数」として表すことは不可能である。

　「<δ,f>とは、「気持ち」としては∫δ(x)f(x)dxを表している。」と書いたが、逆に言うと、普通の関数であって局所可積分関数(すなわち、任意のコンパクト集合Kにおける積分∫_K |g(x)|dxの値が有限値に収束するような関数g)は、性質の良い関数f∈Fに対して値<g,f>=∫g(x)f(x)dxを対応させるF上の線形写像と見なすことができる。この写像は連続性を持ち、超関数の定義を満たすことがわかっている。よって、普通の局所可積分関数gは超関数と見なすことができる。この意味で、超関数は通常の関数の拡張概念であると思うことができる。

　一方で、超関数は特定の点での値を定義しない。気持ちとしては積分で挟んだ値なので、この意味では関数の拡張概念というよりはむしろ、「測度」の拡張であるといったほうがよい。（参考文献[1]）実際、超関数は英語で「distribution」という。再翻訳すれば「分布」なので、関数というよりは「重み付きの体積≒測度」というイメージのある言葉になっている。

　なお、超関数でよく知られているものには「シュヴァルツの超関数」と「佐藤の超関数」があるが、この記事でいう超関数は前者のものである。

「∆G＝δ」の意味を明らかにする

　以上の準備を基に、謎の等式「∆G=δ」の種明かしに入ろう。右辺が超関数である以上、これは超関数の等式である。すなわち、任意のf∈Fを作用させてその値が両辺で等しいなら、この等式が成立していることになる。そこでf∈Fを作用させてみる。右辺はδをfに作用させるのだから、f(0)になる。左辺はどうなるであろうか。左辺は超関数なのではあるが、いったん「普通の関数」だと思って、fをかけて積分してみよう。fは台がコンパクト、すなわち十分遠方（あるいは、領域の境界の近く）で0であるような関数であるから、部分積分を各成分について2回行うと、

∫∆G(x)・f(x)dx = ∫G(x)・∆f(x) dx

となる。すなわち、この右辺は<G, ∆f>に等しい。もちろん、この結果はGを「普通の関数」と見なしてこそ得られる結果なのではあるが、逆に、超関数の微分は「部分積分ができるように」定義される。すなわち、超関数Gを第i成分x_iで偏微分した超関数∂_i Gを、

<∂_i G, f> = -<G, ∂_i f>  (f∈F)

によって定義する。fはC^∞級であるから、右辺は意味を持つことに注意してほしい。このようにすれば、もとの等式∆G=δの意味は、任意のf∈Fに対して、

<G, ∆f> = f(0)

が成立するということである。こうしてみれば、単に微分方程式として手渡された等式「∆G=δ」の曖昧な部分がなくなっている。これは、超関数の意味で初めて成立する式なのである。

　解析学では、微分方程式に性質の良い関数を噛ませて積分することで、超関数の意味で解を定義することがしばしばあり、その意味での解を微分方程式の「弱解」という。滑らかな関数の空間など、関数の連続性に立脚した集合の範囲で解を考えるのは、関数解析の道具を使う際に困難を生じさせることがある。それよりも、2乗可積分関数の空間(L^2空間)など、積分に立脚した関数空間で考えたほうが、関数解析学の応用も容易であり、柔軟な考察が可能となる。ただし、このような積分により定まる空間は、不連続な関数をたくさん含んでいるので、微分演算に関する議論は難しくなる。超関数を利用することで、微分可能性を性質の良い関数に押し付けるのである。

　グリーン関数の場合も同様であり、1点だけに分布するソースが生み出す場を計算しようとすると現れる方程式は「普通の関数」による微分方程式では書けないが、超関数の方程式とみれば意味を持たせることができるのである。そういうわけで、「∆G＝δ」には通常の関数の偏微分方程式にはない手続きが含まれている。電磁気学以外でも、例えば弾性体力学などでグリーン関数のアイデアを何度も使うし、デルタ関数や、同じく超関数として定義される「1/xをかけてコーシーの主値積分」なども使われることがある。ゆえに、このあたりの数学的事情はもっと強調して教えてもらいたいと学生の立場からは思ったのだが、時間が足りなくなってしまうのだろうか。

　実際、ローラン・シュヴァルツが超関数の理論の整備における業績でフィールズ賞を受賞したのは1950年であり、デルタ関数やグリーン関数のアイデアが物理で使われるようになってから数学で正確に意味を与えられるまでには時間を要した。それだけに、数学としてそれ自体深い考察に基づいて緻密に整備された理論である。ただ、我々は偉大な20世紀の先人が生み出した道具を当たり前のように使っていかなければならないわけで、せめてこれくらいの種明かしは一般的な講義や教科書にあってよいと思える。このような思いのもと、この記事を書くことにした。

実際に「∆G＝δ」を確かめてみよう

　最後に、この記事を具体例でおさらいしよう。領域が3次元ユークリッド空間R^3であるときに、関数G(x)=-(4π|x|)^(-1)を超関数とみなしたときにグリーン関数の定義式∆G=δを満たすことを証明してみる。そのためには、∆G=δの両辺をコンパクトな台を持つC^∞級関数f∈Fに作用させた式「<G,∆f>=f(0)」が、任意のf∈Fについて成立することを確かめればよい。すなわち、

を示せばよい。この式の左辺はx=0で特異性を持つ関数の積分であるが、極座標に変換するとこの特異性は消えて、意味を持つ積分であることがわかる。とはいえ、分母に|x|がある以上、x=0のまわりでの被積分関数のふるまいには注意しなければならない。そこで、左辺の全空間R^3の積分を、原点x=0を中心とする半径εの球体での積分と、その外側での積分に分ける。すなわち、

後者の積分は特異性を持たないので、部分積分(ベクトル解析のガウスの発散定理)を2回用いて、

となる。x=0を除いて∆(1/|x|)=0であるので２つの境界項だけが残る。また、S_εはB_εの境界、すなわち半径εの球面である。そして、nはS_εの外向き単位法線ベクトルである。(外部領域におけるストークスの定理なので、面積分の項の符号の違いに注意する）このうち、第1項は次のように評価して、極座標に変換すればO(ε)のオーダーであることがわかる：

　第1行から第2行への変形は、ベクトルの内積に対するコーシー・シュワルツ不等式を使っている。そして、||∇f||=sup|∇f(x)|はベクトル値関数∇fの絶対値の、全空間における上限である。（fはコンパクトな台を持つから、∇fもコンパクトな台を持ち、この上限は有限である）一方第2項は、実際にナブラ演算子のところを計算し、外向き法線ベクトルがn=x/εで与えられることに注意すれば、

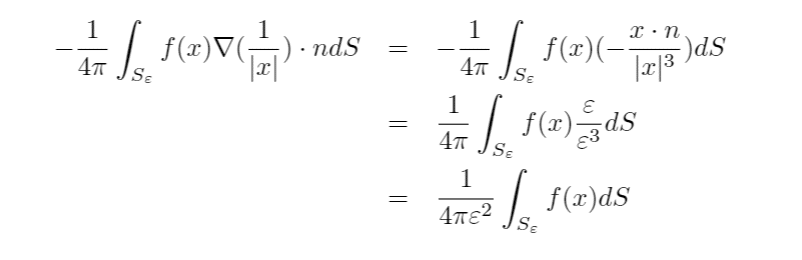
ここでfがx=0で連続であることを用いると、任意のη>0について、あるξ>0が存在して、|x|<ξ ならば |f(x)-f(0)|<ηとなるから、

ε→+0として、さらにηは任意の（いくらでも小さくてよい）正の数だから、前式の値がf(0)に近づくことがわかる。

次に、半径εの球体での積分を評価しよう。次のように評価すれば、この積分がO(ε^2)のオーダーであることがわかる。fはコンパクトな台を持つC^∞関数なので、∆fも有界であることに注意。

以上をまとめると、

となる。以上の計算から、ε→0とすることで示したい等式が証明される。

まとめ

　電磁気学などに現れるラプラス方程式のグリーン関数の定義としてよく現れる「∆G＝δ」は通常の関数の偏微分方程式ではなく、超関数の意味での等式である。超関数は性質の良い関数から数への連続的な線形写像であり、一般の関数で局所可積分なものは超関数とみなすことができる。気持ちとしては「かけて積分する写像」である。

　超関数の等式「∆G＝δ」は両辺を任意の性質の良い関数fに作用させた「<G,∆f>=f(0)」という式が成立することを意味しており、領域がR^3の場合、局所可積分関数G(x)=-(4π|x|)^(-1)はこの等式を満たす超関数とみなせる。

参考文献

[1]楕円型・放物型偏微分方程式　村田實、倉田和浩著　岩波書店(2006)