
bzip2を読む ブロックソート6
こんにちは、junkawaです。
本記事では、前回に続きブロックソートアルゴリズムの「巡回行列のソート」についてソースコードを交えて紹介します。
前回の記事
bzip2を読む はじめに
bzip2を読む ブロックソート1
bzip2を読む ブロックソート2
bzip2を読む ブロックソート3
bzip2を読む ブロックソート4
bzip2を読む ブロックソート5
前回までのおさらい
巡回行列のソートでは、先頭2バイトが異なる行について、クイックソートを行います。
クイックソートはある程度ソートが完了した後で、シェルソートに切り替えます。
本記事では、シェルソートの実装について紹介します。
シェルソート
シェルソートは mainSimpleSort() で行います。ソート中の比較関数 は mainGtU()です。
mainGtU()では、2つの行の全てのシンボルを比較して大小の比較を行います。
ソースコード紹介
mainGtU()@blocksort.c
https://github.com/junkawa/bzip2/blob/master/bzip2-1.0.6/blocksort.c#L338
〜
https://github.com/junkawa/bzip2/blob/master/bzip2-1.0.6/blocksort.c#L469
mainSimpleSort()@blocksort.c
https://github.com/junkawa/bzip2/blob/master/bzip2-1.0.6/blocksort.c#L472
〜
https://github.com/junkawa/bzip2/blob/master/bzip2-1.0.6/blocksort.c#L555
mainGtU()
338: /*---------------------------------------------*/
339: /*--- The main, O(N^2 log(N)) sorting ---*/
340: /*--- algorithm. Faster for "normal" ---*/
341: /*--- non-repetitive blocks. ---*/
342: /*---------------------------------------------*/
343: 同じ値やパターンが繰り返されない場合(一般的な場合)、早いそうです。
同じ値やパターンが繰り返される場合は、fallbackSort()を行います。
計算量は N^2 log(N)とのことですが、詳しく検討できていません。
344: /*---------------------------------------------*/
345: static
346: __inline__
347: Bool mainGtU ( UInt32 i1,
348: UInt32 i2,
349: UChar* block,
350: UInt16* quadrant,
351: UInt32 nblock,
352: Int32* budget )
353: {
i1
入力:比較対象の先頭インデックス。block[i1]から比較を始めます。
i2
入力:較対象の先頭インデックス。block[i2]から比較を始めます。
block
入力:入力データブロック
quadrant
入力:同じ入力文字、同じ入力パターンが連続する場合、比較に時間がかかるが、これを避けて高速に比較できるようにする情報。
nblock
入力:blockのサイズ。block[0..nblock]。nblockは最大で900,000。
budget
入力、出力:同じ入力文字、同じ入力パターンが連続する場合、クイックソートだと時間がかかるので、別のソート方法(fallbackSort())に切り替える必要がある。そのためのカウンタ。8バイト一致したら1減ります。
戻り値
True i1 の行がi2の行より大きい
Flase i1 の行がi2の行より小さい
i1 の行とi2の行が全て一致
354: Int32 k;
355: UChar c1, c2;
356: UInt16 s1, s2;
357:
後で紹介します。
358: AssertD ( i1 != i2, "mainGtU" );
i1とi2が同じ場合、アサートします。
比較対象のi1とi2は違う必要があります。仮に同じ場合、全てのシンボルが一致し、比較に時間がかかってしまいます。
359: /* 1 */
360: c1 = block[i1]; c2 = block[i2];
361: if (c1 != c2) return (c1 > c2);
362: i1++; i2++;
block[i1]とblock[i2]を比較し、値が異なる場合、block[i1] が block[i2]より大きい場合Trueを返し、小さい場合Flaseを返します。
値が同じ場合、次の文字を比較します。
以下、/* 1 */ の処理を12回繰り返します。
12という回数は、歴史的経緯で決定された値だと思われます。
経験的にこれが一番高速だったのでしょうか。
bzip2の最初のバージョン0.9.0では、1バイト比較の6回となっています。
0.9.5dでは、2バイト比較の6回。
1.0.0以降では、1バイト比較の12回になっています。
0.9.0のソースコードftp://ftp.gefoekom.de/pub/really_old_stuff/unix/tools/archiver/bzip2-0.9.0.tar.gz
0.9.5dのソースコード
ftp://ftp2.piotrkosoft.net/pub/mirrors/squid-www/contrib/seafood/SW/bzip2-0.9.5d.tar.gz
1.0.0のソースコード
https://mirrors.slackware.com/slackware/slackware-7.1/source/a/bzip2/bzip2-1.0.0.tar.gz
363: /* 2 */
364: c1 = block[i1]; c2 = block[i2];
365: if (c1 != c2) return (c1 > c2);
366: i1++; i2++;
367: /* 3 */
368: c1 = block[i1]; c2 = block[i2];
369: if (c1 != c2) return (c1 > c2);
370: i1++; i2++;
371: /* 4 */
372: c1 = block[i1]; c2 = block[i2];
373: if (c1 != c2) return (c1 > c2);
374: i1++; i2++;
375: /* 5 */
376: c1 = block[i1]; c2 = block[i2];
377: if (c1 != c2) return (c1 > c2);
378: i1++; i2++;
379: /* 6 */
380: c1 = block[i1]; c2 = block[i2];
381: if (c1 != c2) return (c1 > c2);
382: i1++; i2++;
383: /* 7 */
384: c1 = block[i1]; c2 = block[i2];
385: if (c1 != c2) return (c1 > c2);
386: i1++; i2++;
387: /* 8 */
388: c1 = block[i1]; c2 = block[i2];
389: if (c1 != c2) return (c1 > c2);
390: i1++; i2++;
391: /* 9 */
392: c1 = block[i1]; c2 = block[i2];
393: if (c1 != c2) return (c1 > c2);
394: i1++; i2++;
395: /* 10 */
396: c1 = block[i1]; c2 = block[i2];
397: if (c1 != c2) return (c1 > c2);
398: i1++; i2++;
399: /* 11 */
400: c1 = block[i1]; c2 = block[i2];
401: if (c1 != c2) return (c1 > c2);
402: i1++; i2++;
403: /* 12 */
404: c1 = block[i1]; c2 = block[i2];
405: if (c1 != c2) return (c1 > c2);
406: i1++; i2++;
407:
/* 1 */ の処理を12回繰り返します。
408: k = nblock + 8;
409:
ここで、nblockに8を加算している理由は不明です。
410: do {
411: /* 1 */
412: c1 = block[i1]; c2 = block[i2];
413: if (c1 != c2) return (c1 > c2);
まず、c1とc2で比較を行い、一致した場合、
414: s1 = quadrant[i1]; s2 = quadrant[i2];
415: if (s1 != s2) return (s1 > s2);
quadrantを使って比較を行います。
quadrantは、mainSort()のStep 3でセットされます。
ここでは、quadrantの簡単な紹介にとどめます。
(quadrantについては、mainSort()のStep 3で詳しく紹介します。)
c1(=c2)のシンボルから始まる行がすでにソート済みの場合
ブロック番号i1、i2はptr上でソート完了しています。
つまりptr上での i1の位置と、i2の位置を比べれば、以降のシンボルを比較しないでも、結果が分かることになります。

図では、説明を簡単にするためにシンボルをアルファベットにしています。実際は0〜255のシンボルです。
mainGtU()にて、block[88]以降とblock[198]以降を比較します。
先頭12バイトが一致したので、13バイト目を比較しています。
13バイト目(block[100]とblock[2100])が ‘b’ で一致しました。ここで、’b’から始まる行がすでにソート済みであると仮定します。'b'から始まる行がソートされた時、mainSort()のStep3にて、quadrantに ‘b’から始まる行についてptr上でのインデックスがセットされます。
block[100]から始まる行はソートの結果、ptrのインデックス70、block[2100]から始まる行はptrのインデックス40にソートされたとします。つまり、block[2100]から始まる行の方がblock[100]から始まる行より小さい、です。
quadrant[100]には70、quadrant[2100]には40がセットされます。
quadrantを使うことで、ブロック番号(100,2100)から、ptr上での位置(=比較結果)を得ることができます(quadrantを使わずに、ptr上を探索しても同様のことはできますが、時間がかかり本末転倒となるので、事前にセットしています)。
ソースに合わせて説明すると、i1が100、i2が2100。
c1が’b’、c2が’b’。s1が70、s2が40。100と2100以降を比較しなくても、この時点で以降の比較結果をquadrantから知ることができます。
c1(=c2)のシンボルから始まる行がソート済みでない場合
quadrantは初期値の0のままです。
したがって、quardant[i1]とquadrant[i2]はどちらも0となり、次の文字を比較することになります。
416: i1++; i2++;先頭12バイトの比較にquadrantを使わない理由は不明です。
先頭12バイトで同じシンボルが続く確率が低いため、quadrantを使わずに処理を高速化しているのでしょうか。
417: /* 2 */
418: c1 = block[i1]; c2 = block[i2];
419: if (c1 != c2) return (c1 > c2);
420: s1 = quadrant[i1]; s2 = quadrant[i2];
421: if (s1 != s2) return (s1 > s2);
422: i1++; i2++;
423: /* 3 */
424: c1 = block[i1]; c2 = block[i2];
425: if (c1 != c2) return (c1 > c2);
426: s1 = quadrant[i1]; s2 = quadrant[i2];
427: if (s1 != s2) return (s1 > s2);
428: i1++; i2++;
429: /* 4 */
430: c1 = block[i1]; c2 = block[i2];
431: if (c1 != c2) return (c1 > c2);
432: s1 = quadrant[i1]; s2 = quadrant[i2];
433: if (s1 != s2) return (s1 > s2);
434: i1++; i2++;
435: /* 5 */
436: c1 = block[i1]; c2 = block[i2];
437: if (c1 != c2) return (c1 > c2);
438: s1 = quadrant[i1]; s2 = quadrant[i2];
439: if (s1 != s2) return (s1 > s2);
440: i1++; i2++;
441: /* 6 */
442: c1 = block[i1]; c2 = block[i2];
443: if (c1 != c2) return (c1 > c2);
444: s1 = quadrant[i1]; s2 = quadrant[i2];
445: if (s1 != s2) return (s1 > s2);
446: i1++; i2++;
447: /* 7 */
448: c1 = block[i1]; c2 = block[i2];
449: if (c1 != c2) return (c1 > c2);
450: s1 = quadrant[i1]; s2 = quadrant[i2];
451: if (s1 != s2) return (s1 > s2);
452: i1++; i2++;
453: /* 8 */
454: c1 = block[i1]; c2 = block[i2];
455: if (c1 != c2) return (c1 > c2);
456: s1 = quadrant[i1]; s2 = quadrant[i2];
457: if (s1 != s2) return (s1 > s2);
458: i1++; i2++;
459:
/* 1 */ を8回繰り返します。
460: if (i1 >= nblock) i1 -= nblock;
461: if (i2 >= nblock) i2 -= nblock;
462:
ここでやっと、blokck[nblock-1]を超えた場所を参照した場合の対応をしていいます。
ここまで nblock を超えて参照したかをチェックしなかったのは、処理の高速化が原因だと思われます。
どれだけblock[nblock-1]を超えるか、図示します。

呼び出し元のdは最大15となっています(先頭2バイトの計数ソート分とクイックソートの13バイト分を超えた時)。
呼び出し元が、比較対象の要素数hi-loが20未満となって本関数を呼び出す時には、dは14以下かもしれません。呼び出し元が、先頭からの一致シンボル数が14より多い場合に本関数を呼び出す場合、dは15となっています。
呼び出し元のptr[i]の値は、最大nblock-1となります。また、本関数の先頭12バイトの比較と、ループ初回時の8バイトの比較で、計35バイト分、block[nblock-1]からオーバーしています。
これを考慮して、mainSort() 796行目では、事前に34バイト(BZ_N_OVERSHOOT)分、block[nblokc]〜block[nblock+BZ_N_OVERSHOOT-1]まで、block[0]〜block[BZ_N_OVERSHOOT-1]の値をコピーしています。
463: k -= 8;
464: (*budget)--;
8バイト一致したら、budgetを1減らします。
呼び出し元で、budgetが負数になっていることが確認できたら、一致するシンボルが多すぎるということで、fallbackSort()に切り替えます。
465: }
466: while (k >= 0);
467:
kの初期値がnblock+8なので、nblock+8 -> nblock -> nblock-8 … となり、kが負数になると、全てのシンボルが一致したとして比較終了します。
なぜnblock+8から始まるのか不明です。k=nblockとしても、全てのブロックについて比較できます。データキャッシュに関連する高速化のためでしょうか。
468: return False;
比較対象の行の全てのシンボルが一致した場合、Falseを返します。
469: }
470:
471:
mainSimpleSort()
472: /*---------------------------------------------*/
473: /*--
474: Knuth's increments seem to work better
475: than Incerpi-Sedgewick here. Possibly
476: because the number of elems to sort is
477: usually small, typically <= 20.
478: --*/
479: static
480: Int32 incs[14] = { 1, 4, 13, 40, 121, 364, 1093, 3280,
481: 9841, 29524, 88573, 265720,
482: 797161, 2391484 };
483:
incs配列はシェルソートの間隔です。
シェルソートの間隔はいくつか提案されているのですが、ここでは、Knuth's increments を採用しています。
mainSimpleSort()を呼び出す時は、ソート対象の数がMAIN_QSORT_SMALL_THRESH(20)未満としています。この場合Incerpi-Sedgewickの間隔 (1,3,7,21,48,112,...)より、Knuthの間隔がよいそうです。
484: static
485: void mainSimpleSort ( UInt32* ptr,
486: UChar* block,
487: UInt16* quadrant,
488: Int32 nblock,
489: Int32 lo,
490: Int32 hi,
491: Int32 d,
492: Int32* budget )
493: {
ptr
入力:ptr[lo..hi]の範囲で、ブロック番号 ptr[i] (block[ptr[i]]) から始まる(巡回行列の)行をソートする。
出力:ソート結果をptrに格納する。
block
入力:入力データブロック
quadrant
入力:同じ入力文字、同じ入力パターンが連続する場合、比較に時間がかかるが、これを避けて高速に比較できるようにする情報。
nblock
入力:blockのサイズ。block[0..nblock]。nblockは最大で900,000。
lo
入力:ソート対象の、ptr の下限インデックス。
hi
入力:ソート対象の、ptr の上限インデックス。
d
入力:文字列中の比較文字の位置。
budget
入力、出力:同じ入力文字、同じ入力パターンが連続する場合、クイックソートだと時間がかかるので、別のソート方法(fallbackSort())に切り替える必要がある。そのためのカウンタ。
494: Int32 i, j, h, bigN, hp;
495: UInt32 v;
496:
以下で説明します。
497: bigN = hi - lo + 1;
498: if (bigN < 2) return;
499: bigNが1となるのは、hi と lo が同じ時です。この時、ソートする必要はないので、すぐに関数を抜けます。
500: hp = 0;
501: while (incs[hp] < bigN) hp++;
502: hp--;
503:
シェルソートの間隔の初期値を決定します。
incs配列中の値で、bigNより小さい中で、一番大きな値を間隔とします。
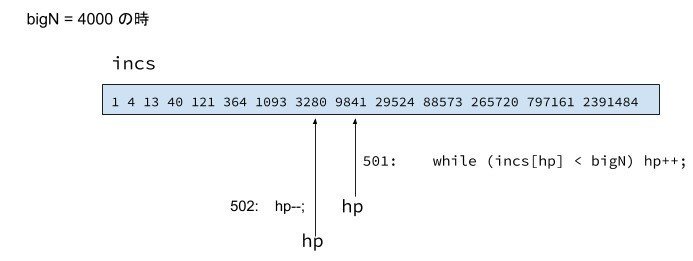
bigN = 4000 の時、incs[hp] は3280 を指します。
504: for (; hp >= 0; hp--) {
hp=0、つまり間隔が1(incs[0]は1)でソートするまで、ループを回します。
505: h = incs[hp];
506: シェルソートでは、間隔hを徐々に狭めていきます。hpが小さくなるにつれ、間隔incs[hp]も小さくなります。

図では4色しか表示していませんが、h=3280の場合3280色、h=1093の場合1093色あります。同じ色の要素間でソートを行います。
このように、間隔をだんだん狭めてソートすることで、最後のh=1でのソートを高速に終えることができます。
507: i = lo + h;
比較の基準値 block[ptr[i]+d] i の初期値を lo+h とします。
508: while (True) {
509:
lo+h〜hi の範囲で、間隔hで要素間をソートします。

図は、h=1093、lo=300の場合です。507行目より、i = 1393。
図中の上段は、i = 1393 の時です。
510〜523行の copy 1 では、512行目で v = ptr[1393]。514行目でmainGtU(ptr[300]+d, v+d,...)を比較し、517行目で大きい方をptr[1393]に入れ、521行目で小さい方をptr[300]に入れています。
図中の中段は、522行目で i = 1394とし、同様にcopy 2 を行った場合です。
図中の下段は、508のwhileループを繰り返し、i = 2486 ( lo+2*h)になった場合です。
この時、ptr[300]+d、ptr[1393]+d、ptr[2486]+d間でソートを行います。300、1393間はすでにソート済み(i=1393の時)です。
まず v = ptr[2486]で、ptr[2486]とptr[1393]をmainGtU(ptr[1393]+d, v+d,...) で比較します。ptr[1393]+dの方が小さい場合、mainGtU()はFalseを返すので、514行目のwhileループには入りません。この時、ptr[300]+d、ptr[1393]+d、ptr[2486]+d間はソート済みとなるため、2489の値を入れ替える必要はありません。
ptr[1393]+dの方が大きい場合、514行目のwhileループに入り、517行目でptr[1393]の値をptr[2486]に入れます。また、次のwhileループでptr[300]+dとv+dを比較します。ptr[300]+dの方が大きい場合、517行目でptr[300]の値をptr[1393]に入れます。そして521行目でptr[300]にvを入れます。ptr[300]+dの方が小さい場合、whileループには入らず、521行目でptr[1393]にvを入れます。結果として、ptr[300]+d、ptr[1393]+d、ptr[2486]+d間はソート済みとなります。
510: /*-- copy 1 --*/
511: if (i > hi) break;
比較対象の要素がなくなったら(hiを超えたら)、whileループを抜けます。
512: v = ptr[i];
513: j = i;下記では、v を ptr[j]、ptr[j-h]、ptr[j-h*2]、ptr[j-h*3] … の中で適当な場所に挿入します。
514: while ( mainGtU (
515: ptr[j-h]+d, v+d, block, quadrant, nblock, budget
516: ) ) {ptr[j-h]とvの0からd-1までのシンボルは同じ値です。
mainGtU()では、ptr[j-h]+d 、v+d 以降のシンボルを行の最後まで比較していきます。
ソートの比較では、-1、0、1を返すことが多いですが、ここでは、True、Falseが返ってきます。
ptr[j-h]+d以降のシンボルの方が大きい場合、Trueが返ります。v+d以降のシンボルの方が大きい場合、またはptr[j-h]+d以降とv+d以降のシンボルが全て一致した場合、Falseが返ります。
以下の処理は、ptr[j-h]+d以降のシンボルの方が大きい場合となります。
ソートでは、シンボルが大きい方を ptr の後方に置きます。
517: ptr[j] = ptr[j-h];ptr[j-h] を後方(ptr[j])に移動します。
518: j = j - h;間隔h離れた要素を比較対象にします。
519: if (j <= (lo + h - 1)) break;間隔h離れた要素がない場合、ループを抜けます。
520: }
521: ptr[j] = v;v を、適切な場所(ptr[j])に挿入します。
522: i++;
523: 次の要素(ptr[i])を、比較対象とします。
524: /*-- copy 2 --*/
525: if (i > hi) break;
526: v = ptr[i];
527: j = i;
528: while ( mainGtU (
529: ptr[j-h]+d, v+d, block, quadrant, nblock, budget
530: ) ) {
531: ptr[j] = ptr[j-h];
532: j = j - h;
533: if (j <= (lo + h - 1)) break;
534: }
535: ptr[j] = v;
536: i++;
537: copy 1と同じです。
538: /*-- copy 3 --*/
539: if (i > hi) break;
540: v = ptr[i];
541: j = i;
542: while ( mainGtU (
543: ptr[j-h]+d, v+d, block, quadrant, nblock, budget
544: ) ) {
545: ptr[j] = ptr[j-h];
546: j = j - h;
547: if (j <= (lo + h - 1)) break;
548: }
549: ptr[j] = v;
550: i++;
551: copy 1と同じです。
552: if (*budget < 0) return;budgetがなくなったら、呼び出し元に戻ります。
(fallbackSort()に切り替えます)
553: }
554: }
555: }
556:
557: まとめ
クイックソートから呼び出されるシェルソートについて紹介しました。これで先頭2バイトの値が異なる行についてのソートが完了しました。
次回は、先頭2バイトが同じ値となる行のソートについて紹介します。
ご覧下さりありがとうございます。いただいたサポートは図書館への交通費などに使わせていただきます。
