【数学】「み・は・じ」から始める微分積分

こんにちは、Junです。

今日は、微分積分を小学校5年生あたりで習う「み・は・じ」から解説していこうと思います。

1．み・は・じ

皆さんは、小学校5年生の頃に、以下のような図を見たことがあると思います。

それぞれを式に起こすと、

となります。

ここで、距離（道程）をx、速さ（速度）（※）をv、時間をtとおくと、

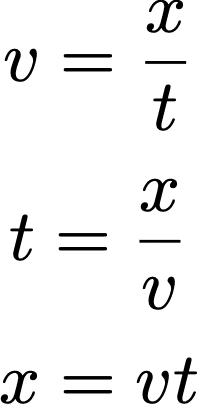
となります。

※数学や物理学において、速度と速さは厳密には異なるもとですが、ここでは混乱を避けるために「速さ」という表現を使うことにします。

2．距離と時間から速さを求める

100kmを2時間で走行したとき、速さは時速何kmか？

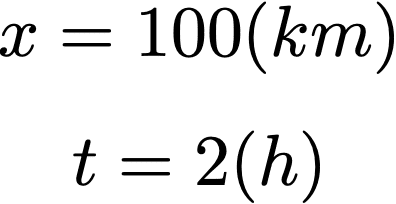
であるから、求める速さは

この状況を、横軸に時間t、縦軸に距離xを取ってグラフにすると以下のようになります。

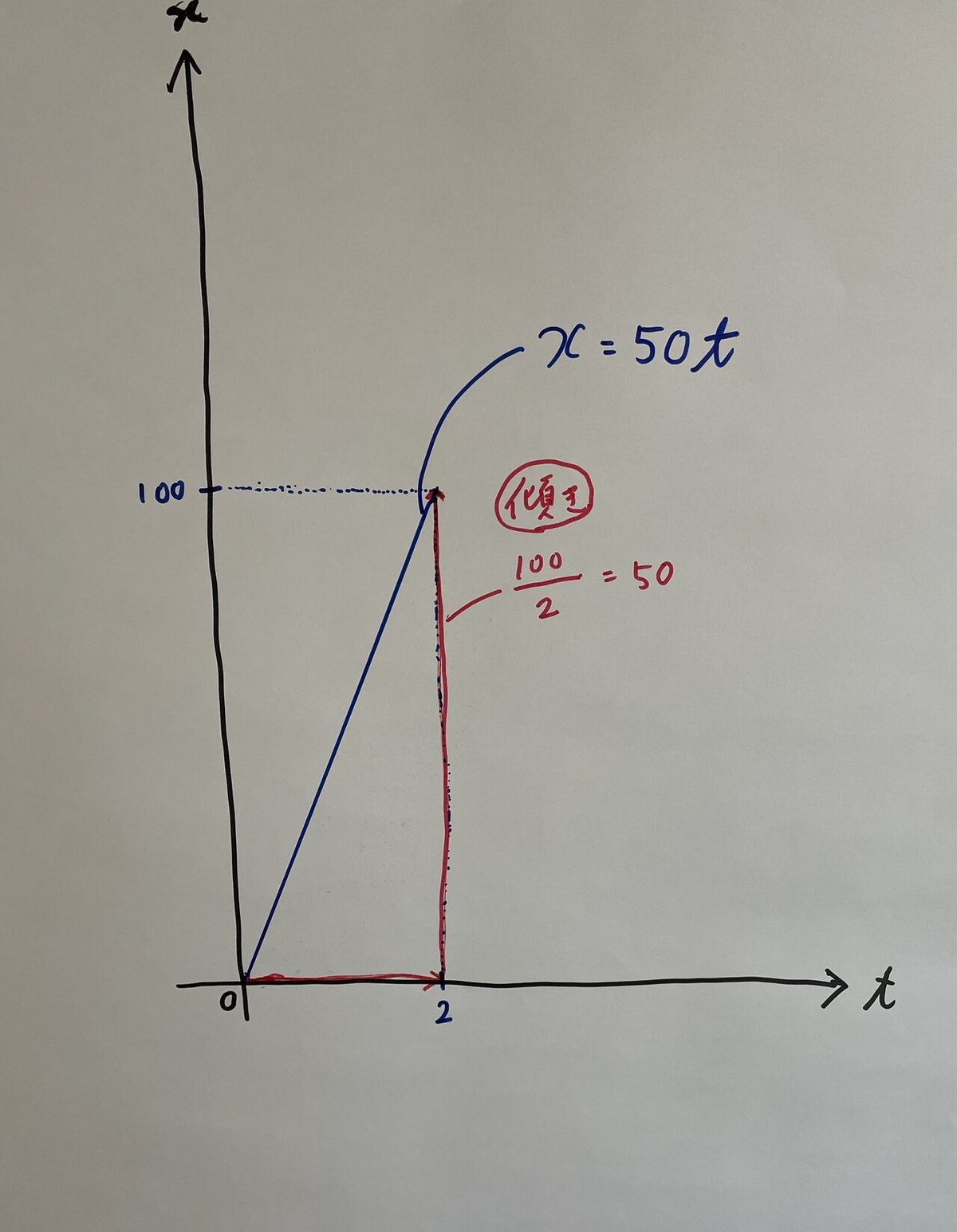
このグラフにおいて、速さは傾きにあたります。

このグラフの傾きは常に一定です。

3．速さ（速度）を求める⇨微分する

では、距離xと時間tの関係が以下のような状況にある場合はどうでしょうか？

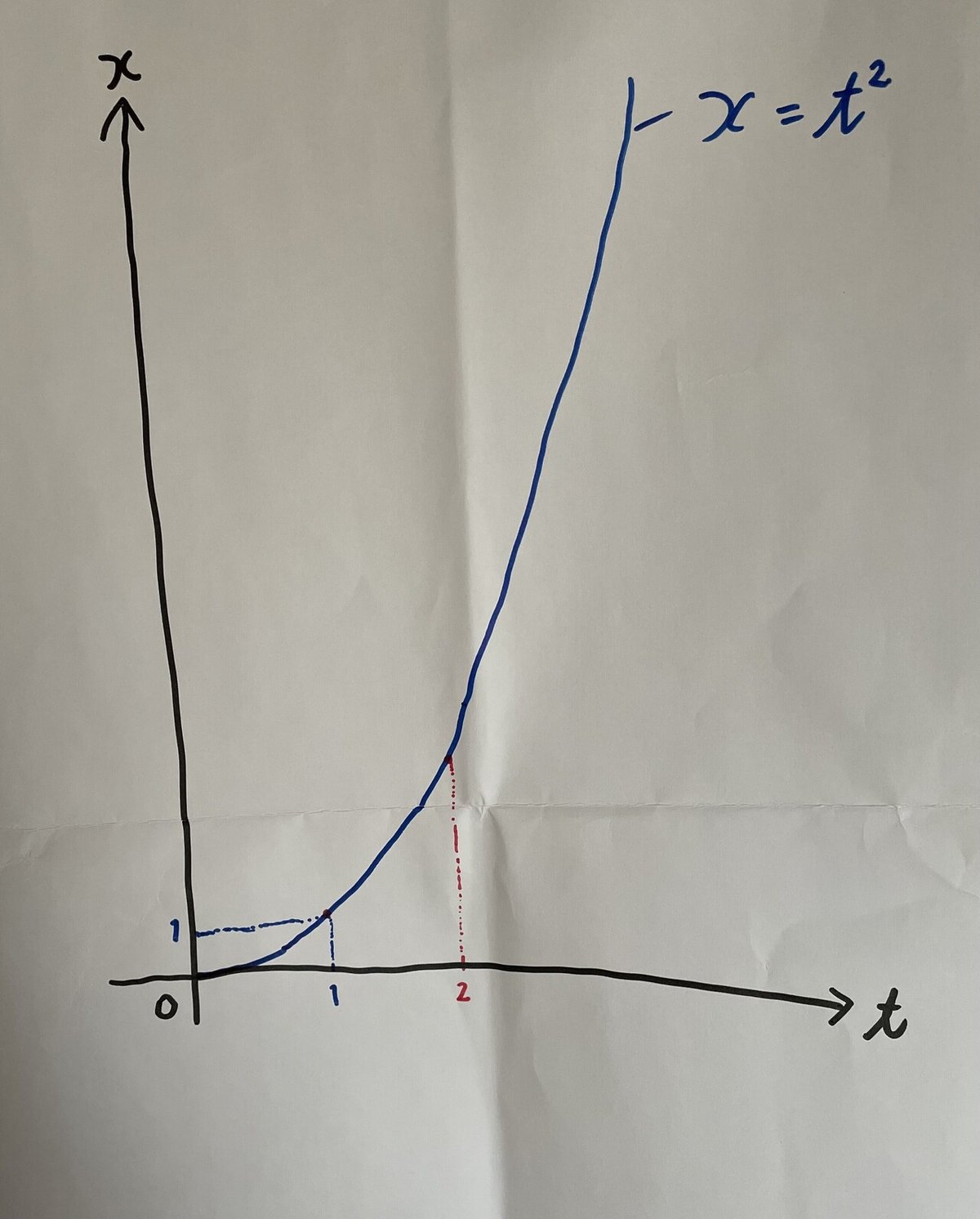
という関係が成り立っているとするとき、まず、t=1とt=2を結ぶ直線の傾きを求めると、

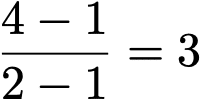
となります。

しかし、今回は、どの2点を取るかによって、傾きの値が変化します。
つまり、今回は一定の速さでは走っていません。

ここで、t=2における速さ（傾き）を求めたい。

つまり、以下における、接線の傾きを求めたい。

しかし、この1点において、

時間0、距離0なので、

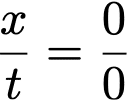
となってしまい、値が定りません。（不定形といいます）

そこで、以下のように考えてみます。

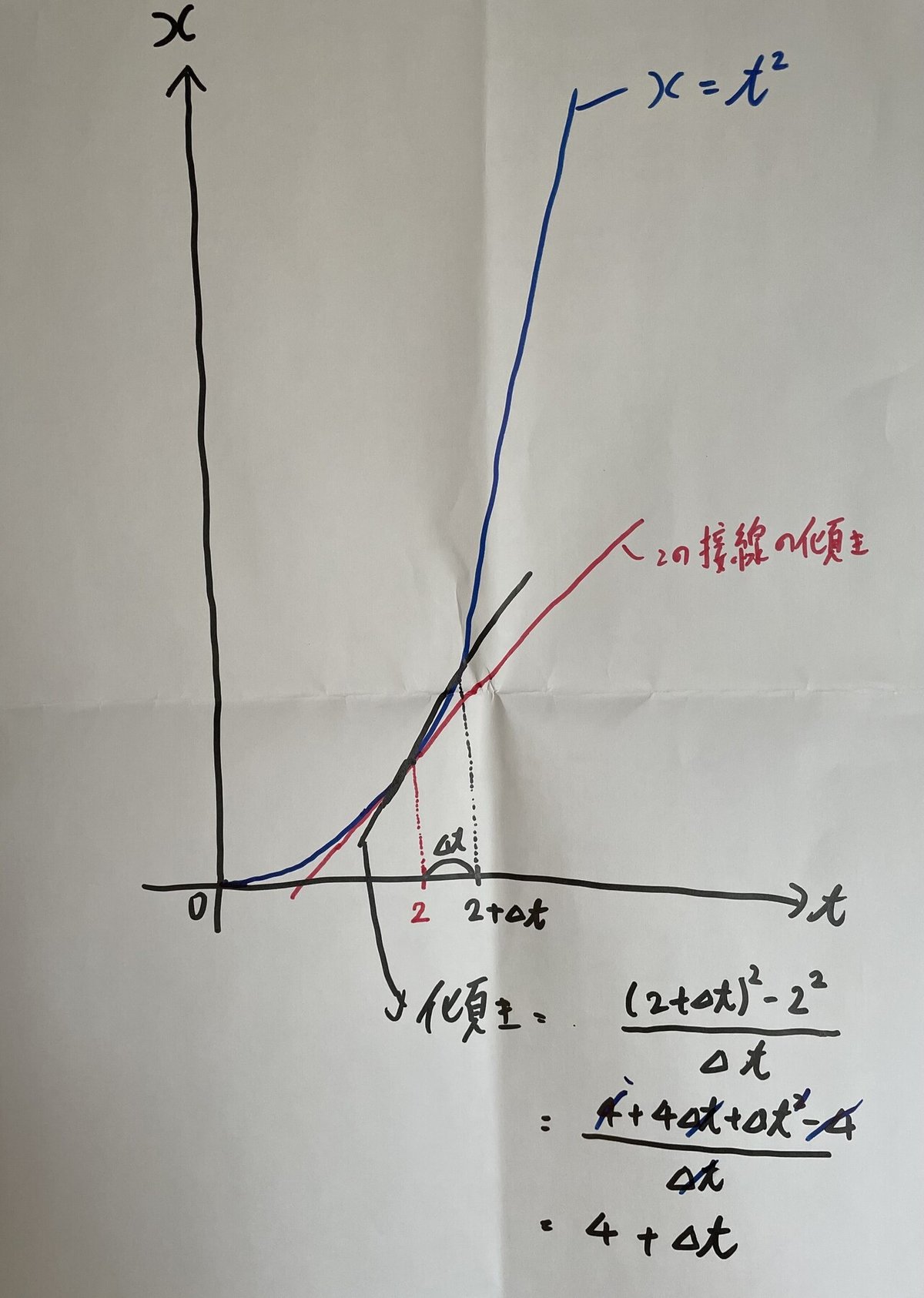
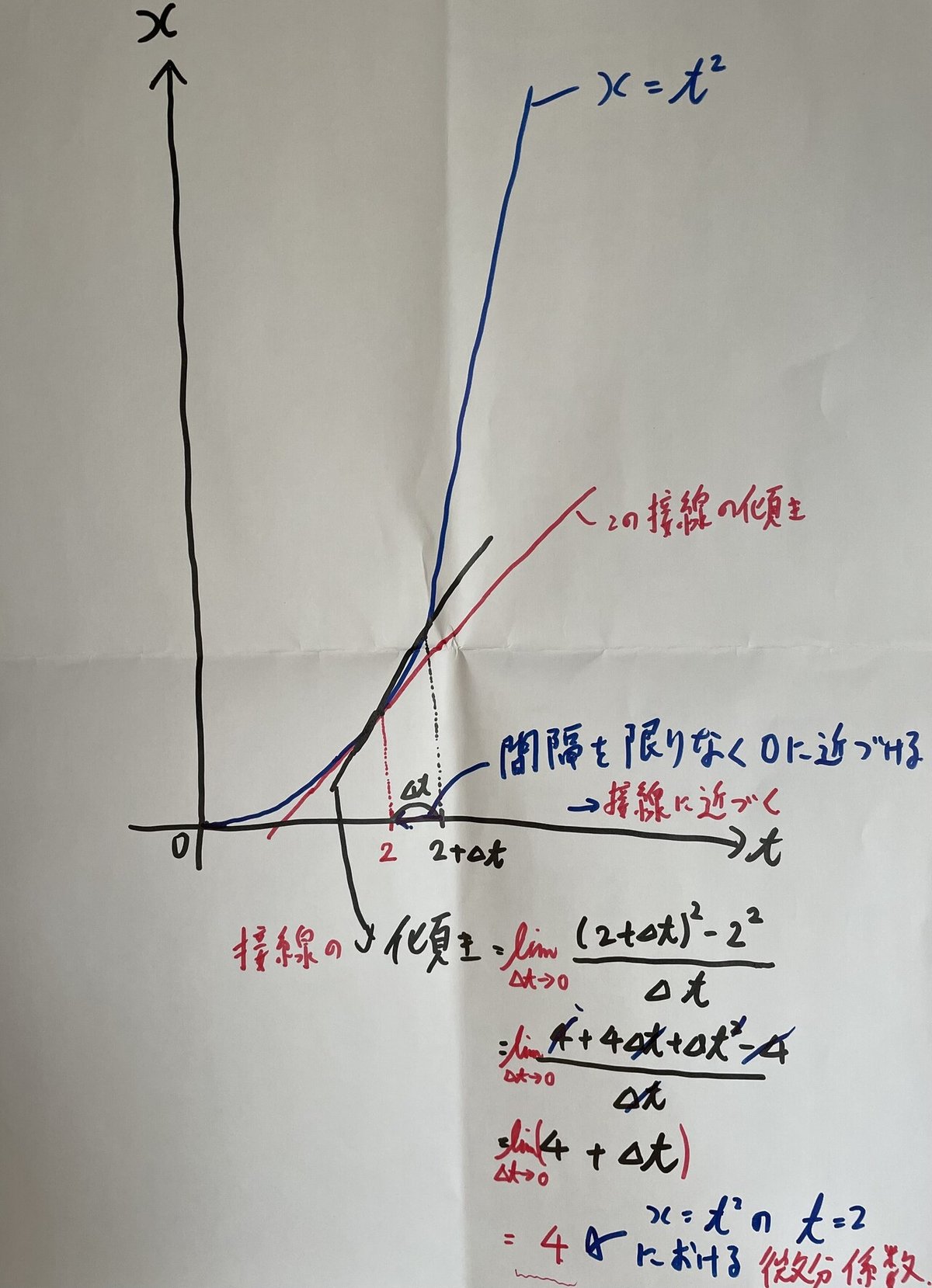
t=2から、Δtだけ離れたところにt=2+Δtを取ると、傾きは以下のように表せます。

そして、このΔtの値を限りなく0に近づけていくと、接線の傾きに近づきます。

これを、以下のような式で書きます。

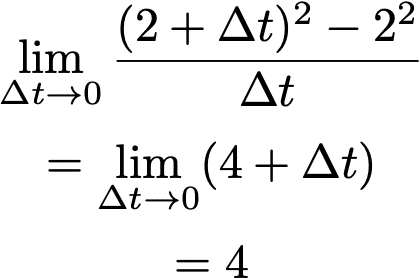
これより、接線の傾きが4であることがわかります。

この接線の傾きのことを微分係数といいます。

そして、これを任意の実数tについて定義した

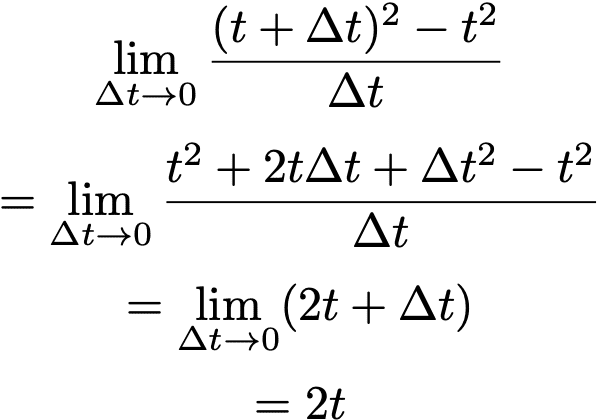
を

の導関数といい、これを求めることを微分するといいます。

そして、この導関数を

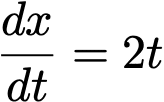
または、

と書きます。

4．速さと時間から距離を求める

100km/hで2時間走行したとき、何km走行したことになるか？

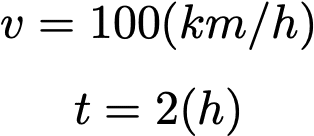
であるから、求める走行距離は、

この状況を、横軸に時間t、縦軸に速さvを取ってグラフにすると以下のようになります。

このグラフにおいて、距離は斜線部の面積にあたります。

つまり、速さvと時間tから、距離xを求めることは、面積を求めることになります。

では、速さが一定でない場合を考えます。

まずは、以下のように速度が変化する場合を考えます。

この場合は、以下の△OABの面積を求めれば良いので、

4kmとなります。（v軸の単位はkm/h、距離は4kmで(/h)は要りませんでした）

5．距離を求める⇨面積を求める⇨積分する

では、速さが以下のように変化する場合はどうでしょうか？

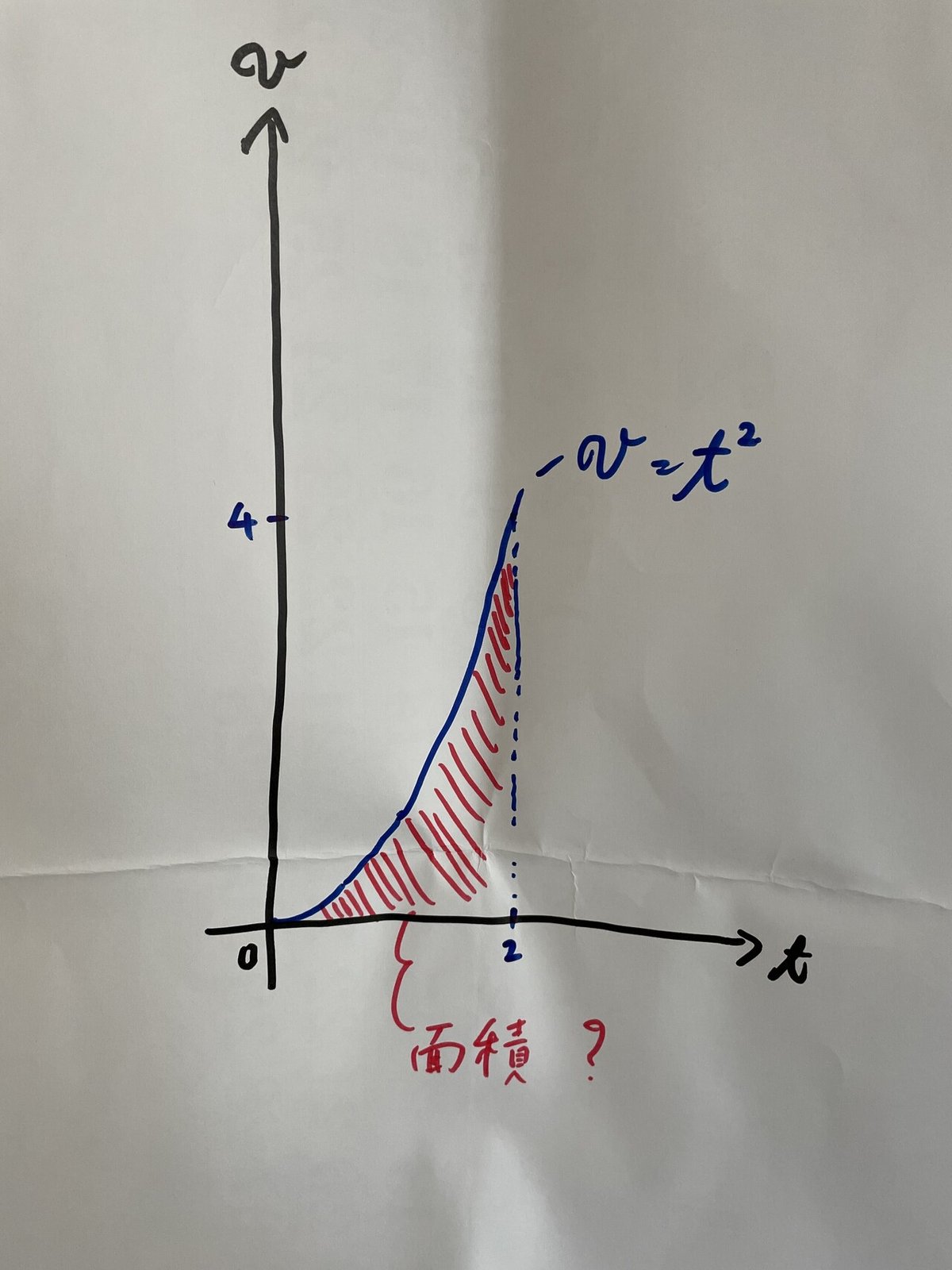
これまでの知識では、この斜線部の面積を求めることができません。
つまり、距離を求めることができません。

そこで、以下のように、グラフ上に長方形を描いていきます。

そうすると、k番目の長方形の面積は、

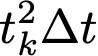
1番目の長方形からn番目の長方形を足すと、

このnを限りなく大きくしていくと、Δtの間隔がどんどん小さくなっていき、斜線部の面積に近づきます。

これを、以下のように書きます。

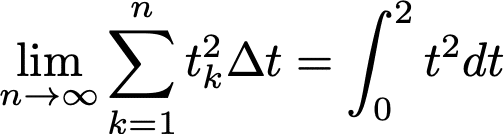
このことを、関数v=t^2を、0から2まで積分するといいます。
※これが定積分の定義です。

6.原始関数

さて、ここからどのように計算すれば良いでしょう？

距離から速さを求めるときは「微分」し、
速さから距離を求めるときは「積分」します。

つまり、微分と積分は逆演算であることがわかります。

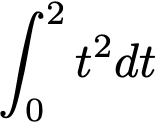
の計算をするためには、t^2の微分する前の形を知る必要があります。
この関数を原始関数といいます。

ここで、t^3を微分してみましょう。

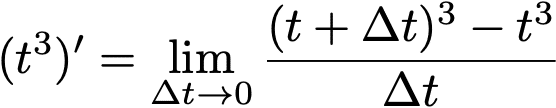
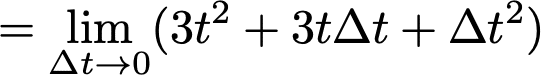
すなわち、

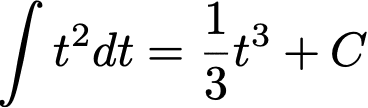
Cは積分定数（定数項を含んでいる場合も微分して同じ関数になるため）

これが、t^2の原始関数です。

この原始関数は面積を表しています。

これのt=0から2までの区間の面積を求めるので、

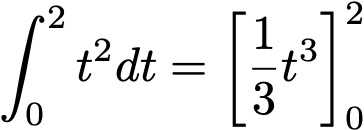
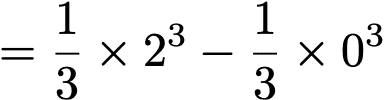
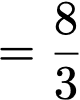
※定積分の場合、引き算によって積分定数Cが消えてしまうので、書きません。

この計算により、8/3(約2.3)km走行したことになります。

7.まとめ

微分積分と聞くと、難しそうに思えるかもしれませんが、このように紐解いていくと、特別難しいことをしているわけではなく、これまで習ってきた計算を抽象化しただけだということを抑えれば、比較的習得しやすいのではないかと思います。

次回は、様々な関数の微分積分について書いていこうと思います。

#数学がすき #みはじ #はじき #道程 #距離 #速さ #速度 #時間 #傾き #微分 #面積 #積分 #導関数 #原始関数