
【機械学習初学者向け】検索システム・ランキング学習の基礎知識まとめ
三菱UFJフィナンシャル・グループ(以下MUFG)の戦略子会社であるJapan Digital Design(以下JDD)でMUFG AI Studio(以下M-AIS)に所属している松本 尭之(まつもと たかゆき)です。2022年12月に三菱UFJ銀行からJDDに出向し、現在は銀行業務のAI活用支援に従事しています。
今回は、R&Dとして調査した「ランキング学習の基礎」について、共有させていただきます。
背景
検索エンジンは、もはや生活の一部となっています。
誰もが知るGoogleを始めとして、HP内での情報検索、企業内で独自開発した検索エンジンなどもあります。
私の出向元である三菱UFJ銀行にも、社内利用を目的とした検索エンジンがあり、手続きの検索や、冠婚葬祭にあたる諸々の申請方法を調べるなど、用途は多岐に渡ります。
気軽に情報検索ができることは大変ありがたい一方で、欲しい結果が得られないことも度々あります。
「MUFG版「ChatGPT」の開発秘話」にもあるように、LLM導入により情報検索が容易になり、今後検索エンジンを使う機会は減るかもしれません。
とはいえ、検索エンジンを全く使わなくなることも、遠い将来の話に思えますので、「行内検索エンジンの精度改善」を見据え、今回は「ランキング学習の基礎」について調査した内容を共有いたします。
なお、検索エンジンそのものを実装する場合、大規模なシステム構成が必要になります。
ユーザが検索を行うインターフェースや、検索クエリと文書を紐づけしたデータを格納するためのデータベースは多岐に渡りますが、
本記事では、検索システムにおける、「検索ランキングモデル」および「ランキング学習」について説明します。

用語集
通常の機械学習では、あまり聞き馴染みのない言葉が出てきます。私自身、少し混乱したので、以下に本記事で使う用語をまとめます。
検索ランキングモデル:検索エンジンにおけるランキングにて使用する、機械学習モデルのことを指す。単に、ランキングモデルと記載されることもある。
ランキング学習:検索ランキングモデルの学習のこと。LTR(Learning to Rank)と記載されることもある。
検索クエリ:ユーザが検索するときの単語や文。単にクエリと記載されることもある。
関連度:クエリに対する文書の関連度合いを示したもの。二値(関連がある/関連がない)、または多段階の数値で示される。後者の場合、数字が高いほど関連性が高い。
ユーザインターフェース:ユーザが操作する画面。検索クエリの入力や、検索結果の閲覧を行う。
インデクサ:文書のデータ取得、適する形式への加工、インデックス登録を実施する。
ランキング学習の流れ
ランキング学習は、以下の流れで実装します。
訓練データを用意
訓練データの前処理・特徴量追加
検索ランキングモデルの学習・評価
検索システムへの組込
以降、上記3より評価指標・アルゴリズムについて詳説いたします。
1〜2は、既存のデータセットを利用する前提とします。また4は、検索システム全体の話になるため、本記事では割愛します。
評価指標
まず、ランキング学習に利用される評価指標について紹介します。
再現率(recall / recall@k)
再現率は、ユーザが欲しい文書を取りこぼしなく検索結果に表示できたかを図る指標です。
検索エンジンにある全文書のうち、ユーザの検索意図と一致する文書を集合Aとします。
ここで、検索結果に表示した文書を集合Bとしたとき、
「AとBに共通する文書 ÷ A = 再現率」となります。
例えば、「みかん ゼリー」と検索して、10件ヒットしたとします。
10件のうち、4件がみかんゼリーに関する文書で、6件が桃ゼリーに関する文書を表示しました。
このとき全文書のうち、みかんゼリーに関する文書が8件あるとしたら、再現率は 4÷8=0.5 となります。
また、ランキング学習では、上位表示される文書に注目します。というのも、ユーザは検索結果の上位のみ確認することが多いからです。
そこで、上位k件に注目したrecall@kを利用することもあります。
さきほどのゼリーの例において、上位3位に表示された文書のうち、みかんゼリーに関する文書が2件だとします。すると、recall@3 は 2÷8=0.25 になります。
適合率(precision / precision@k)
適合率は、ユーザが欲しい情報だけを検索結果に表示できたかを示す指標になります。再現率とは異なり、検索意図にマッチした情報のみ表示することを重視しています。
先ほどの集合A(=検索エンジンにある全文書のうち、ユーザの検索意図と一致する文書)、集合B(=検索結果に表示した文書)で説明すると、
「AとBに共通する文書 ÷ B = 適合率」となります。
前述の「みかん ゼリー」の具体例においては、10件ヒットしたとき、4件がみかんゼリーに関する文書だったので、適合率は 4÷10=0.4 と計算できます。
なお、上位k件に注目した、precision@kを利用することもあります。
平均適合率(Average Precision)
precision@k を求めるにあたり、どのようなkが最適な値なのか分からない際に利用するのが、平均適合率(Average Precision)です。
検索結果に表示された文書(=先ほどの集合B)より、1件目から順にprecision@kを求めます。
求めたprecision@kの平均が、平均適合率になります。

MAP(Mean Average Precision)
前段で求めた平均適合率は、1つの検索クエリに対して求めた値でした。
しかし、複数のクエリを用いて性能を評価することが一般的です。そこで求めるのが、MAPです。
求め方は単純で、複数クエリで算出した平均適合率の平均値をとります。
逆数順位(Reciprocal Rank)
検索クエリに関連する文書が、上位表示されるほど精度がよいというのは、直感的に感じる部分だと思います。
その対となるものとして、逆数順位(Reciprocal Rank)は、クエリに関する文書が検索結果の最初に提示された順位の逆数をとったものになります。
少し複雑なので、具体例を用います。
異なる2つのランキングモデルから、以下のように10個の文書が得られたとします。

モデル①では、1件目に関連する文書があるので 1÷1=1 と逆数順位が求められます。また、モデル②も同様に1件目に関連する文書があるため、逆数順位が1となります。
しかし、ここで1つ注意が必要です。
1〜10位の全体をみると、モデル①のほうが1〜3位に関連する文書が集中しており、性能が高いことが分かります。
このように、あくまでも「ユーザのニーズを満たす文書が1つ発見できれば良い」という前提のもと有用な指標であることが注意すべき点です。
MRR(Mean Reciprocal Rank)
逆数順位も1つの検索クエリに対する評価指標です。
そこで、複数クエリに対しては、それぞれで求めた逆数順位の平均値となるMRR(Mean Reciprocal Rank)をとります。
考え方は、MAPと同じとなります。
CG(Cumulative Gain)
前述の評価指標は、いずれも検索クエリに対して「関連がある」「関連がない」の二値ラベルを付与した上で、利用する指標でした。
CGは、二値ではなく多段階の関連度を付与した上で利用できます。
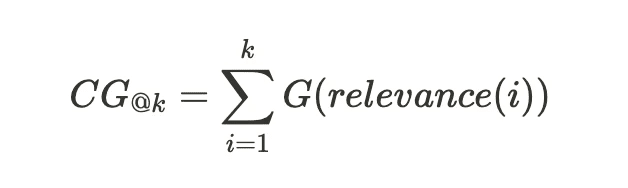
relevance(i)は、i番目の検索結果に付与された「検索クエリとの関連度」を示します。
G(y)は、CG@kを計算するにあたり、関連度の重みづけをする関数です。
※G(y)において、yそのものに意味はなく、数式を表現するための記号になります。したがって、y = relecance(i)と考えてください。

上記の計算式が利用されることが多いです。
なお、文書の表示順位が変わっても、CGの値にはなんら変化がありません。そのため、次に紹介する評価指標を用います。
DCG(Discounted Cumulative Gain)
繰り返しになりますが、CGの計算では文書の順位を気にしません。
しかし、「上位表示されるか?」という点も考慮すべきです。そこで、順位の高低も考慮するのが、DCGになります。

η(i)は、文書の順位に応じたペナルティです。下位文書ほどペナルティが大きく、

上記が使われることが多いです。
nDCG(Normalized DCG)
DCGを0〜1の範囲に正規化したものです。
これによって、異なるアルゴリズムを使った場合でも、精度の比較ができるようになります。

ここでいうiDCGとは、最も関連度の高い文書が上位にくるときの理想的なDCGになります。
少し分かりづらいので、具体例を使って説明します。
あるランキングモデルから、以下のような結果が得られたとします。

上記より、DCGを算出すると、以下のように求まります。

関連度が高い文書ほど、表示順位も高くなると以下のようになります。

この時のDCG(=iDCG)を求めます。

以上より、nDCG = 7.518 ÷ 9.824 = 0.765 と求まります。
評価指標のまとめ
以下に、紹介した評価指標をまとめます。

アルゴリズム
続いて、ランキング学習に利用されるアルゴリズムを紹介します。
基本の3種(ポイントワイズ・ペアワイズ・リストワイズ)
ランキング学習においては、目的関数の選び方から大きく3つに分類することができます。
ポイントワイズ法
検索クエリに対応する各文書に対して、関連度そのものを予測するように学習します。ペアワイズ法
検索クエリに対応する文書のペアに対して、関連度の大小を予測するように学習します。リストワイズ法
検索クエリに対応する文書のリストに対して、関連度の順序を予測するように学習します。
以下より、上記3種に類するアルゴリズムを紹介していきます。
PRank(ポイントワイズ法)
文書の分類を目的とした、単純パーセプロトンを用いたポイントワイズ法の1つです。
入力層→出力層の重みと、ランキングを決めるための閾値を学習・予測をします。単純で実装しやすい反面、線形非分離な問題においては、精度が低い傾向にあります。
RankNet(ペアワイズ法)
多層パーセプトロンを用いたペアワイズ法の1種で、様々なアルゴリズムの元ネタになっています。
2文書(文書A・文書B)において、「文書Aが文書Bより高順位である確率」と「真の確率」の交差エントロピー誤差を最小化することで順序を予測し、これを繰り返すことで文書全体の順序関係を導きます。
しかし、順位を直接予測するものではないため、「誤差は小さいが、順位が異なる」事態が発生します。
そこで上記を踏まえ、後続のLambdaRank、LambdaMARTが生まれることになります。
LambdaRank(ペアワイズ法)
こちらも多層パーセプトロンを用いたペアワイズ法の1種です。
RankNetで順位を直接予測できないことを受け、LambdaRankでは評価指標(nDCG、MRRなど)を用いた損失関数を定義し、順位を予測します。
nDCGを使う場合は、2文書を入れ替えた際のnDCG差の絶対値をとり、損失関数を定義します。
LambdaMART(ペアワイズ法)
LambdaRankに、MART(Multiple Added Regression Trees)という勾配ブースティングのアルゴリズムを適用した、ペアワイズ法の1つです。
決定木を複数組み合わせたアンサンブルであり、勾配ブースティングの特徴でもある「スケーリング不要」「欠損値があっても処理可能」は有効です。
また、LightGBMやXGboostなど、多くのGBDT系モデルで簡単に利用することができます。
ListNet(リストワイズ法)
多層パーセプトロンを用いたリストワイズ法の1つです。
順列確率(Permutation Probability)という、「文書のランキングの尤度を示した確率」を使い、損失関数を定義します。
RankNetでは、文書ペア単位の損失関数を使ったのに対し、ListNetではリスト単位の損失関数を使います。したがって、文書数が2つのとき、ListNetの損失関数は、RankNetと等しくなります。
ただ、配列関数は総乗であらわされ、求める順位が多いほど計算量も膨れ上がります。これを防ぐために、ランキングtop1のみに絞った配列関数を使うことが多いです。
アルゴリズムのまとめ
以下に、紹介したアルゴリズムをまとめます。
なお、記載したアルゴリズムの派生系も含めると膨大な数のアルゴリズムがある点はご留意ください。

最後に
ここまで読んでいただき、ありがとうございます。
主に、ランキング学習における評価指標・アルゴリズムについて紹介しました。
書籍やネット記事などを拝見する限り、評価指標についてはnDCGを利用することが多いように見受けられました。
場合によっては、2段階のランキングモデルを用意し、1段目モデルで再現率から最適化→2段目モデルで適合率から最適化というケースもあります。各段階の狙いとしては、以下の通りです。
1段目:「検索クエリに関連する文書を取りこぼしなく得る」こと。
2段目:「1段目の結果から、検索クエリに関連する文書を正確に得る」こと。
これにより、より関連度の高い文書を表示できる可能性があります。

また、アルゴリズムについては、基本的にはListNetなどのリストワイズ法に類するアルゴリズムを利用し、データセットの有無や、解決したい問題の複雑さから、他アルゴリズムを利用する印象です。
Google, Yahooを始めとして、検索システムは私たちの生活に浸透しきっています。
浸透しているが故に、検索システムの仕組みやランキング学習を意識する機会は、滅多にないと思います。正直に申し上げると、ここまで膨大な知識や技術がでてくるとは思ってもいませんでした。
ところが、本記事の執筆にあたり、検索システム並びにランキング学習という分野の一端を垣間見ることができました。
また、LLM(大規模言語モデル)にも通じる点もありました。
私個人としては、今後の発展性も高いと思うため、次回の記事では、紹介した内容をもとに実験した結果を共有できればと思います。
参考資料
ランキング学習について記載された書籍
ランキング学習について記載されたブログ
アルゴリズムに関して記載されたブログ
アルゴリズムに関して記載された論文
Japan Digital Design株式会社では、一緒に働いてくださる仲間を募集中です。カジュアル面談も実施しておりますので、下記リンク先からお気軽にお問合せください。
この記事に関するお問い合わせはこちらにお願いします。
M-AIS
松本 尭之
