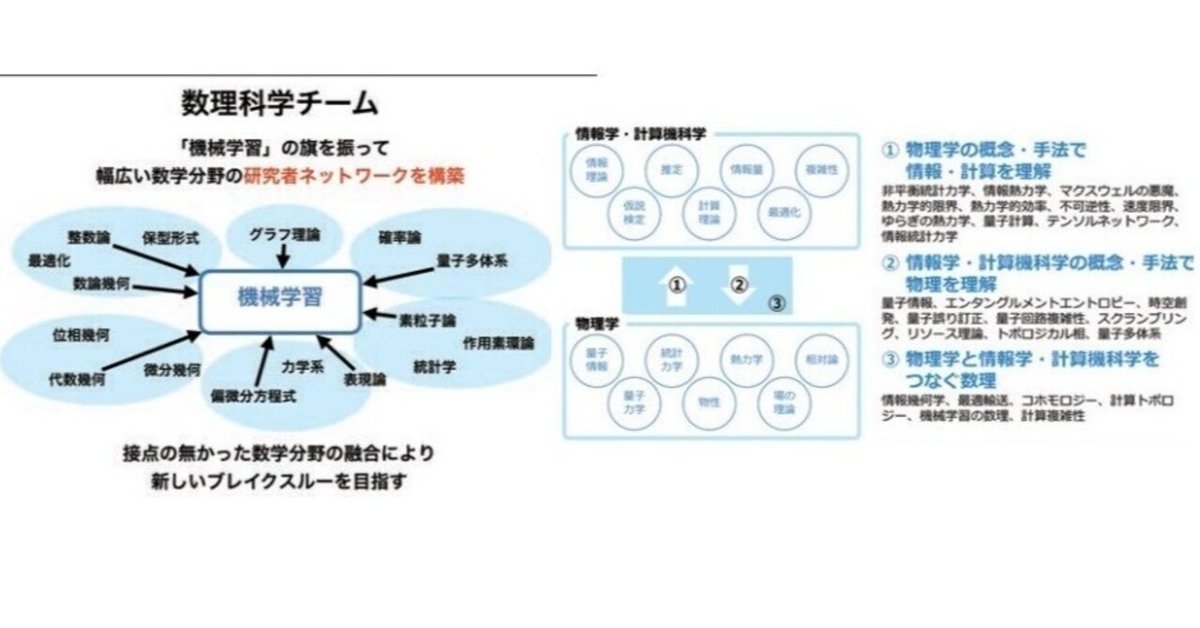
(資料集)情報熱力学・情報幾何学関連
情報熱力学・情報幾何学関連の資料集です(*'▽')
どなたかのご参考になれば幸いです( *ˊᵕˋ* )
〇東京大学 大学院理学系研究科 生物普遍性研究機構 伊藤 創祐 准教授
・ERATO「沙川情報エネルギー変換プロジェクト」
・学術変革領域研究B「量子効果によるエネルギー生成/利用の革新的効率向上法の開拓と実現」
・新学術領域研究「情報物理学でひもとく生命の秩序と設計原理」
これまでの研究
・ネットワーク上の情報熱力学
・E.coli走化性シグナル伝達の情報伝達と情報熱力学
・ゲーム理論的な情報熱力学
・情報幾何とゆらぎの熱力学, 情報熱力学
・化学熱力学とゆらぎの熱力学のアナロジー
・最適輸送理論とゆらぎの熱力学、Wasserstein幾何学
・population dynamicsにおける情報幾何的な速度限界
・確率過程, 決定論的な化学反応系における
熱力学的散逸の幾何学的な分解と熱力学的トレードオフ関係
・相関関数の非対称性と非平衡性の間の普遍的な関係
・非平衡性による緩和の振る舞いに関する熱力学的な限界
・流体系における熱力学とゆらぎの熱力学とのアナロジー
・脳ダイナミクスにおける脳波に対する熱力学的な不可逆性の周波数分解
・パターンダイナミクスにおける最適輸送と、
熱力学的な散逸とパターン変化のトレードオフ
・生成AI(機械学習・人工知能)の手法である
拡散モデルにおける生成精度の熱力学的な限界
・情報幾何と最適輸送理論の関係の数理的展開
・“情報理論と小さな系の熱力学”
https://sosuke110.com/NoteBenkyokai.pdf
第 1 章 情報理論入門 2
1.1 確率分布 . 2
1.2 Shannon entropy (シャノンエントロピー...... 3
1.3 Relative entropy (Kullback-Leibler divergence, 相対エントロピー) .... 4
1.4 相互情報量 (Mutual information... 7
1.5 Communication channel (通信路... 9
1.6 Noisy-channel coding theorem (シャノン第二定理.... 11
1.7 まとめ ... 14
第 2 章 情報理論と小さな系の熱力学 17
2.1 詳細ゆらぎの定理(Detailed fluctuation theorem.... 17
2.2 エントロピー生成 (Entropy production...... 19
2.3 フィードバック制御下での小さな系の熱力学 ..... 21
2.4 小さな “部分系”の数学的記述: Bayesian network ... 25
2.5 小さな “部分系”の熱力学: ネットワーク上の情報熱力学 ........ 29
2.6 まとめ, 今後の展望 ........ 36
・熱・統計力学と数学 ~ 熱・統計力学と情報理論・情報幾何の関係を例にして ~
https://sosuke110.com/surikagaku2023.pdf
平衡統計力学におけるカノニカル分布
平衡熱力学における Legendre 双対性
平衡状態におけるゆらぎと応答
結びに代えて - 幾何学と非平衡熱力学
私自身の興味の対象は未だ未完成とされている平衡状態を離れた非平衡・非定常な状態における熱・統計力学を, すでに完成したとされる平衡熱・統計力学の一般化としてどのように構築できるか,ということである.
この一般化の際に重要となるのは, 平衡熱・統計力学における結果の一般化を与えてくれる情報理論・情報幾何の数学だろうと我々は考えている.
なぜならば, これまでみたように平衡状態における確率分布に基づいた「平衡統計力学」の結果や, Legendre 双対性に基づいた「平衡熱力学」の結果は, 「情報理論・情報幾何」の数学の結果の特殊なケースとして理解可能だと言えるからである.
よって, 平衡状態を離れた非平衡・非定常な状態における熱・統計力学も, 何らかの意味で情報理論や情報幾何の数学の助けを借りながら, 物理的に妥当な形で構築することが可能だろうと考えている.
そのような考えのもと, 現在我々が興味を持って取り組んでいる研究は, 情報幾何や最適輸送理論などの情報理論に関係する幾何を用いて, 非平衡熱力学の幾何学的な理論フレームワークを構築することである.
実際, 今までに得られた結果によると, 熱力学的な散逸であるエントロピー生成や, 物理量のゆらぎ, 物理量の期待値の変化速度などは, Fisher 情報量や, Kullback–Leibler ダイバージェンス, Wasserstein 距離などの幾何学的な情報の指標を用いて捉えることができている.
その結果, ある種の省エネルギー性能であったり, もしくは熱力学的な最適化や制御を, 情報の幾何における測地線といったような幾何学的な視点から捉えることができるようになってきた (例えば, 文献14~16)).
このような研究によって非平衡熱力学をある種の「数学化」をすることで, 今まで物理的な事実として知られていた結果を数学的に捉え直すことができ, 拡張や一般化を考えることが容易になった.
さらに様々な幾何学的な不等式や幾何学的な事実を「物理的に」読み替えることで, 非平衡系のダイナミクスにおける物理的な制約や新たな見方を数学から提供できるようになってきた.
・物理学と情報幾何学—ゆらぐ系の熱力学の視点から
https://sosuke110.com/surikagaku2020.pdf
マスター方程式でのゆらぐ系の熱力学(stochastic thermodynamics)
エントロピー生成と Kullback–Leibler ダイバージェンス
射影とエントロピー生成
Fokker–Planck 方程式でのゆらぐ系の熱力学
時間に関する Fisher 情報量とゆらぐ系の熱力学
長さと熱力学的速度制限
時間に関する Fisher 情報量の単調性と定常への緩和
Glansdorff–Prigogine の安定性理論を情報幾何学の視点から捉え直すのが面白いと考えている9).
実際, 安定性理論における過剰エントロピー生成と呼ばれる量と dI(t)/dt の対応関係が成り立つ.
また安定性理論は非線形力学系の視点が導入されているため, 情報幾何学を力学系の視点から考え直すことにつながるだろう.
二つ目は, レート方程式で駆動される化学反応ネットワーク上の化
学熱力学を考えることである10).
このとき Gibbsの自由エネルギーと正測度空間の f-ダイバージェンスが対応づく.
確率分布の規格化の形をしていない保存則による拘束条件が入った正測度空間が考察対象になるため, 情報幾何学的にも新規性があり面白いと思う.
・最適輸送と熱力学的最適化
https://webpark2072.sakura.ne.jp/otworkshop/slide_ito.pdf
・連続状態の確率密度分布の最適輸送
・ブラウン運動における熱力学的最適化と最適輸送
・最適輸送の幾何と情報幾何
・特にブラウン運動を記述するFokker-Planck方程式と最適輸送理論が熱力学でつながっていることに基づき, 熱力学的な散逸(最小エントロピー生成)を達成する最適輸送を考えた.
・L2-Wasserstein距離の空間での速度の二乗に比例する散逸(過剰エントロピー生成率)が,さまざまな熱力学的な最適化に関係する不等式(熱力学的速度限界, 熱力学的不確定性関係)を与えることを示した.
・最適輸送の幾何と情報幾何が結びつくことを, 勾配流による表現による確率分布の情報幾何と, interpolated dynamicsと呼ぶ速度場を変更したダイナミクスの経路の同時確率分布の情報幾何の二つの視点から導出した.
・最適輸送に基づいた熱力学
https://sosuke110.com/ERATOkickoff.pdf
・最適輸送に基づく非保存力と保存力の分解
・最適輸送に基づくエントロピー生成率の分解
※過剰エントロピー生成率と維持エントロピー生成率の分解
・有限時間で最小エントロピー生成を達成する 最適なプロトコルと測地線
・観測量の速さとの関係
・様々な系への拡張 1 - Markov jump系
・様々な系への拡張 2 - 決定論的な化学反応ダイナミクス
・様々な系への拡張 4 - 決定論的な流体ダイナミクス
・情報幾何/情報熱力学との関わり
・維持エントロピー生成率のモード分解の 脳ダイナミクスへの応用
最適輸送理論におけるバリエーションの一つである「有限時間 で連続の式のダイナミクスで輸送する時 に流れに応じたコストがかかる」という問題 (e.g., Benamou-Brenier公式)とその拡張により, 様々な系(e.g., 拡散系, Markov jump系, 決定論的な化学反応系, 反応拡散系, 流体系)における最小エントロピー生成の問 題を取り扱う事ができる。
熱力学における非保存力と保存力による散逸の分解が, 最適輸送理論における最適なプロトコルの考え 方から導入できる。
またその分解によって, 時間変化に起因する散逸(過剰エントロピー生成率)と, 時間 変化を伴わないサイクルによる散逸(維持エントロピー生成率)に分解できる。
時間変化に起因する散逸(過剰エントロピー生成率)は, 系の状態の時間変化に対する制限をトレードオフ 関係(熱力学的不確定性関係/速度限界)の形で与える。
・情報による観測量の変化速度の熱力学的な限界を発見
・熱力学的な観測量の変化速度と情報の抽象的な概念を結びつけることに成功した。
・観測量の変化速度に関する情報による熱力学的な限界を新たに導出した。
・有限の熱コストで機能している生体システムにおいて、この熱力学的な限界が情報処理速度に影響している可能性があるため、生体システムの熱力学的な理解が進むと期待される。
・フォッカー・プランク方程式の幾何熱力学:情報幾何学と最適輸送の間の確率的熱力学的リンク
我々は、非平衡熱力学におけるエントロピー生成率の微分幾何学的側面に関する最近の研究成果を用いて、
非平衡熱力学の幾何学的理論、すなわち幾何熱力学を提案する。
フォッカー・プランク方程式の確率熱力学におけるエントロピー生成率の幾何学的側面に関する最近の研究結果を再検討することにより、情報幾何学と最適輸送理論の観点から非平衡熱力学の幾何学的枠組みを導入する。
提案された幾何学的枠組みは、
熱力学的コストと観測可能な変動との間の熱力学的トレードオフ関係、
最小熱力学的コストのための最適プロトコル、
および非平衡システムのエントロピー生成率の分解など、
いくつかの非平衡熱力学関係を得るのに有用であることを示す。
我々は、確率密度空間における勾配フロー表現と情報幾何学の関係、
および最適輸送における速度場と経路確率密度空間における情報幾何学の関係に基づいて、過剰エントロピー生成率を介して情報幾何学と最適輸送理論との間のいくつかの確率的熱力学的リンクを明らかにした。
・Nonequilibrium Physics : 非平衡科学
https://sosuke110.com/noneq-phys.pdf
第2章 確率過程
2.4 マスター方程式
※量子マスター方程式、Lindblad 方程式
2.5.2 Fokker–Planck方程式
2.5.4 移流拡散方程式とBrown運動
2.7 Langevin方程式
第3章 ゆらぎの熱力学
3.1 流れと力
第4章 情報量とゆらぎの熱力学
4.1 Shannonエントロピーと微分エントロピー
4.2 Kullback-Leiblerダイバージェンス
4.3 Fisher情報行列
4.3.1 情報幾何
4.3.3 Cram´er-Raoの不等式
4.4.3 相互情報量
4.5 エントロピー生成とKullback-Leiblerダイバージェンス
4.6 揺らぎの定理
4.7 詳細釣り合い条件におけるエントロピー生成率とKullback-Leiblerダイバージェンス
4.8 熱力学第二法則と平衡状態の安定性
4.8.1 力学系とマスター方程式
4.8.3 熱力学第二法則と平衡分布の安定性
第5章 力学系と安定性
5.1 確率過程とパラメータの力学系
5.1.1 キュムラントとモーメント
5.1.2 Fokker–Planck方程式とキュムラントの力学系
5.2 レート方程式
5.2.1 化学反応とマスター方程式
5.3 化学熱力学と平衡状態の安定性
5.3.1 平衡状態とエントロピー生成率
5.3.2 Kullback-Leiblerダイバージェンスの一般化とエントロピー生成率
5.4 非線形性と不安定な固定点
5.5 非線型性と分岐
・Geometric decomposition of entropy production in out-of-equilibrium systems
・Information geometry of excess and housekeeping entropy production
・Force-current structure in Markovian open quantum systems and its applications: geometric housekeeping-excess decomposition and thermodynamic trade-off relations
D3の吉村くんと、M1前川くん、D1永山くんとの論文がarXivに上がりました。吉村くんが博論前に急いで書き上げてくれました。GKSL方程式で記述される開放量子系における熱力学(量子熱力学)での流れと熱力学力の定義+etc(エントロピー生成の分解/トレードオフ)の論文です。https://t.co/o9s6hcp1Hc
— Sosuke Ito (伊藤 創祐) (@ito_sosuke) October 31, 2024
熱力学的力と不可逆電流は、古典的非平衡熱力学の基本概念である。
メソスコピック系からマクロスコピック系に至る古典系では、
エントロピー生成率はそれらの積で与えられる。
しかし、量子力学を尊重するそのような構造の完全な量子拡張はない。
本論文では、量子マスター方程式で記述される開放量子系における
勾配構造を伴う電流と力を表す反エルミート演算子を提案する。
エントロピー生成率は力演算子と電流演算子の積で与えられ、
古典系におけるエントロピー生成率の標準表現を拡張することを証明した。
この枠組みは、離散古典系の非平衡熱力学との包括的な類似性を構成する。
また、この構造が確率熱力学におけるいくつかの結果、
すなわちエントロピー生成の幾何学的ハウスキーピング過剰分解や、
熱力学的不確定性関係や散逸時間不確定性関係などの
熱力学的トレードオフ関係の拡張につながることも示す。
トレードオフ関係を議論するにあたり、量子拡散率と呼ぶ変動の尺度を導入します。
・Mondでの質疑応答(最適輸送・情報幾何・化学系・より上位の物理レイヤーなどと間の、それぞれの関連性について)
情報幾何空間はKullback-Leiblerダイバージェンス(KLD)の空間で考えるという話かと思いますが、僕自身はL2-Wasserstein距離空間の相当の話であればKullback-Leiblerダイバージェンスの空間(すなわち情報幾何空間)と
【対応がつく】と考えています。
少なくともLangevin系では対応づきますし
一般の(接続行列でグラフの構造が定義可能な)Markov jump系でも
情報距離空間の話との間で不等式評価ができそうな気配があります。
個人的には、L2-Wasserstein距離相当の空間の方が、
勾配流(gradient flow)という数学的に良い性質があることが知られているので、L2の方が熱力学的には自然だという感覚はあります。
例えば、その自然性の傍証として、
L2-Wasserstein距離相当の熱力学の話(特にgeometric decomposition)は、ダイナミクスに起因する微分演算子に基づく自然な幾何の話なので、例えばNavier-Stokes方程式における流体系の熱力学の話にも拡張が可能です。
(L2-)Wasserstein距離の空間の話だとその勾配は、
勾配流(gradient flow)という形で書かれます。
この勾配流の表現は、情報幾何における勾配である
素朴な確率分布のFisher情報計量ではないですが、一方で
経路の確率に関するFisher情報計量
とは関係し得ます。
またこの濱崎さんの論文における「遷移エネルギー」は
量子系のダイナミクス(Nonlinear Schrödinger equation)に基づいて定義されるもので、素朴にはKullback-Leiblerダイバージェンス(もしくは量子相対エントロピー)で記述される量ではないと考えています。
ただし、L2-Wasserstein距離空間での熱力学の文脈においては、
エントロピー生成率と呼ばれる散逸の量は
Kullback-Leiblerダイバージェンスで記述がされます。
速度限界はどの空間で見るかによって、
時間と対応するコストの量が変わります。
Fisher情報計量で与えられる情報幾何の距離空間での「速度限界」は~~などに代表されるものであり、コストは平衡近傍では仕事のゆらぎなどになる、物理量のゆらぎに関連するものになります。
~~におけるWasserstein距離の世界での「速度限界」とは異なるものです。こちらの世界ではコストは熱力学的散逸を意味するエントロピー生成が出てきます。
よってエントロピー生成という熱力学的な散逸と時間の関係をグラフ上で素朴に扱おうと思うと、L2-Wasserstein距離の世界での「速度限界」が関係してきます。
そもそも「速度限界」の出自は量子性に一切寄らないので、
そもそも最小単位を構成できる気はしませんが、
「固有時間」もしくは「固有速度」みたいなものは確かに
「速度限界」の式から定義可能です。
例えば、情報幾何の空間の話であれば~で与えられるCramér–Rao限界から、~~にあるような「観測量に関する速度」という概念を定義でき、
これは時間に関するFisher情報量であるintrinsic speed
と我々が呼ぶ「固有速度」を常に超えることがないことが、
Cramér–Rao不等式の帰結として出てきます。
なので、これをダイナミクスの「固有速度」ということは可能です。
この「固有速度」の逆数は固有時間とみなすこともできるでしょう。
またWasserstein距離の世界でも同様の「速度限界」から、
Cramér–Rao限界のような限界
(巷で言う熱力学的な不確定性関係、もしくは
Wasserstein-Cramér–Rao不等式)によって
「観測量に関する固有の速度」みたいなものは定義可能です。
Hatano-Sasaエントロピー生成はexcessとhousekeepingがありますが、
特にexcessのHatano-Sasaエントロピー生成は、
定常分布からの相対エントロピーすなわち
Kullback-Leiblerダイバージェンスの時間微分の量で記述が可能です。
例えば、Markov jump系におけるexcessのHatano-Sasaエントロピー生成相当であるnonadiabaticエントロピー生成は、~のように
定常分布と現在の分布の間のKLDの時間微分の形で記述が可能です。
またこの表現はある種のLyapunov安定性とも結びついています。
またこの表現に基づくことで、Markov jump系よりも一般のケース(レート方程式で記述される化学反応ダイナミクス)においても、情報距離の双対空間に基づいて、このHatano-Sasaのexcessエントロピー生成は記述が可能です。
またこの表現は、L2-Wasserstein距離の世界での
勾配流の表現とも関連しており、
定常分布と現在の分布の間のKullback-Leiblerダイバージェンスではなく、連続の式による確率ダイナミクスを記述するときの、
ある種のdivで表される微分演算子における
kernel(核空間)で定義されるような分布
(我々はこれをpseudo canonical distributionと呼んでます)と、
現在の分布の間の
Kullback-Leiblerダイバージェンスの時間微分の形で記述ができます。
また、Langevin系に限ってはHatano-Sasaの
excessエントロピー生成も
housekeepingエントロピー生成も
経路の確率を使うことでKullback-Leiblerダイバージェンスで記述
する方法はあります。
これはHatano-Sasaの原論文や関連などで議論された、
積分型ゆらぎの定理で記述されることから直ちにわかることです。
このJohn Baezの話は基本的にPrice方程式に関係する話だと思います。
Price方程式の話は、基本的に「情報幾何」の「速度限界」の話に相当していて、今まで上げた論文の中では~に対応するものです。
なので、Wasserstein距離の世界の「速度限界」とは異なります。
例えば、「情報幾何」の「速度限界」と関連する話で~がありますが、ここで議論された話はPrice方程式相当であることが指摘されています。
実際、我々はこれに相当する話に基づき、
進化の「速度限界」についての話を情報幾何の空間で行いました。
また、上のプレスリリースの著者である濱崎さんも、
ポピュレーションダイナミクスにおいて
情報幾何の空間での「速度限界」をやっていたかと思います。
そもそも情報幾何の速度制限は
化学反応系の濃度に関する正測度空間に拡張可能なので、
化学反応で記述されうるポピュレーションダイナミクスのような
非線形ダイナミクスにも速度限界は議論可能でした。
さらに、L-2 Wasserstein距離の空間に関係が深いMarkov jump系での
「熱力学的な速度限界」も化学反応系に拡張可能なので、
この論文では、代表的なポピュレーションダイナミクスである
Lotka-Volterra系で我々は「熱力学的な速度限界」を議論しています。
またグラフ上のL2-Wasserstein距離の話は、
この化学反応(もしくはMarkov jump系での)での
「熱力学的な速度限界」の本質的な拡張と位置付けることは可能です。
とこのように、非常に込み入った状況になっているので、
また新たな理解によってこの辺りの話は整理しなおされる可能性
はあります。
〇東京大学大学院 工学系研究科 物理工学専攻 沙川貴大 教授
・ERATO「沙川情報エネルギー変換プロジェクト」
・学術変革領域研究B「量子効果によるエネルギー生成/利用の革新的効率向上法の開拓と実現」
・新学術領域研究「情報物理学でひもとく生命の秩序と設計原理」
・「Maxwellのデーモン」はフィードバック制御によって,第二法則と矛盾はせずに,情報(相互情報量)を仕事・自由エネルギーに変換するデバイスであると理解され,量子情報理論との関係も見出されたことで,現在でも活発な研究対象となっています.
・これらの拡張された第二法則においては,仕事 W や自由エネルギー F などの熱力学変数が,相互情報量 I やShannon情報量 H などの情報量と,対等に扱われる形になっています.
したがって,この拡張第二法則は「情報熱力学の第二法則」と呼びうるものになっています.
また,この結果は,量子と古典の両方の領域に適用できる一般的なものです(量子効果は,自由エネルギーや相互情報量の具体的な表式の中に現れます).
・第二法則が課す限界よりも多くの自由エネルギーを系に獲得させる実験に,世界で初めて成功しました.
これは,微小非平衡系において情報を利用したフィードバックを用いることで,第二法則の制約を超えてエネルギー収支を自在に制御でき,相互情報量を自由エネルギーに変換できることを示した原理実証であると言えます.
・外部パラメータによって駆動される熱力学系において,平衡状態間の遷移に関する熱力学第二法則は,エントロピー生成が非負であると述べることができます.
しかし,非平衡定常状態間の遷移に関する制約は,エントロピー生成が非負であることだけでは十分に特徴づけることができません.
そこで,非平衡定常状態間の遷移におけるエントロピー生成から,定常状態を維持するために必要なエントロピー生成を差し引いた過剰エントロピー生成が,非平衡定常系の熱力学を考えるうえで重要な役割を果たすという議論がこれまでになされてきました.
我々は,有限個の状態をジャンプするマルコフ過程について,準静的過程における過剰エントロピー生成のキュムラント生成関数を,フルオーダーで計算するための一般的な関係式を導きました.
ここで,キュムラント生成関数と量子力学におけるBerry位相との間には数学的な対応があり,キュムラント生成関数はパラメータ空間上の経路だけに依存する幾何学的な量になっています.
この結果に基づき我々は,非平衡定常状態間の遷移において,過剰エントロピー生成を特徴づけるようなスカラー値の熱力学ポテンシャルが一般には存在しないことを示しました.
我々の結果は,非平衡定常状態間の遷移を記述するにはベクトルポテンシャルが必要である可能性を示唆しており,非平衡定常系の性質を解明する上での新たな方向性を示していると考えられます.
・量子測定で得られる測定値のゆらぎには,量子系そのものがもつ量子ゆらぎと,測定に伴うエラーの,二重構造があります.
前者は状態と物理量だけから計算されるものですが,
後者は量子測定のプロセスを考慮して初めて明らかになります.
我々は,量子測定理論と,Fisher情報量など推定理論の概念・手法を用いて,この二種類のゆらぎの構造について研究してきました.
非可換な物理量の間には,量子ゆらぎによって不可避の不確定性関係があります.一方,非可換な物理量を同時に測定すると,測定に伴うエラーの間にも不可避の不確定性関係が生じることが,理論的にも実験的にも知られてきました.
つまり,不確定性関係にも,二重構造があることになります.
たとえば,位置と運動量を同時に測定すると,量子ゆらぎと測定のエラーが同じだけの寄与をして,不確定性関係の下限が通常の二倍になることが知られています.
環境からのノイズがある状況では,量子系に対して理想的な(エラーのない)射影測定を行うことができません.
そのため,ノイズのある状況においてどうやったらできるだけエラーの少ない測定ができるか,ということが,量子情報処理を行う上で問題になります.
我々は,一般の有限次元量子系において,Fisher情報量を尺度として最適な(最もエラーの少ない)測定を明らかにし,そのときに得られる情報量を決定することに成功しました.
・情報処理の熱力学(情報熱力学)
https://noneq.c.u-tokyo.ac.jp/wp-content/uploads/2021/10/natsugaku_Sagawa.pdf
・シラード・エンジン(マクスウェルの悪魔)
・情報理論入門
・ゆらぎの定理と熱力学第二法則
・ランダウア原理(ランダウアーの原理)
・測定とフィードバックの熱力学
・「デーモンのパラドックス」をめぐって
このようにして,デーモンと第二法則の整合性は完全に理解できたわけであるが,これで 情報熱力学の研究が終わったというわけではない.
むしろ逆で,これを出発点にして,多様 な情報処理を含む非平衡ダイナミクスを,現代的観点から研究する途が拓かれたと言える.
定量的なマクスウェルのデーモンの実験は,2010 年に はじめて実現された [2].
その実験では,螺旋階段状のポテンシャルを作り,単一コロイド粒 子をフィードバックによって登らせることに成功した.
そのときの情報から仕事・自由エネ ルギーへの変換効率 (15) は,約 30 %であった.
また最近になって,単一電子による実験で もデーモンが実現されている [45, 46].
それはオリジナルのシラード・エンジンにより近い ものであり,変換効率は 70 %以上を達成している.
またこれらの実験において,フィード バックがある状況でのゆらぎの定理が検証されている.
理論的に興味深いもう一つの方向性は,たくさんの系が複雑に相互作用し,測定やフィー ドバックに限らない複雑な情報の流れがあるときに,情報熱力学をどう拡張するかというこ とである.
このような状況は,ベイジアン・ネットワークという概念で定式化できる(図 7 を参照).
最近,そのようなネットワーク上での情報流と非平衡ダイナミクスを統一的に扱 う形に,ゆらぎの定理や第二法則が拡張された [51].
そこでは,移動エントロピー(transfer entropy)と呼ばれる,情報の流れを表す概念が重要な役割を果たす37.
そのようにして得ら れた第二法則の拡張は,通常の第二法則よりも不等式として真に強いものであることが示さ れている.
さらに,上記の理論はいずれも,生命現象の解析に応用できる可能性を秘めている.
実際,ネットワーク上の情報熱力学を,大腸菌の走化性のシグナル伝達に応用する試みがなされている.
その結果として,大腸菌内での情報流と,ノイズに対する走化性の頑健性の間の,定量的な関係が明らかになった [53].
また,本稿では古典系の場合のみを議論したが,量子系への拡張も可能である [54–58].
その場合は量子情報理論と熱力学の接点が重要になる38.
たとえばエンタングルメント(entanglement)や量子ディスコード(quantum discord)[60] などの量子的な相関は,熱力学第二法則と密接な関係をもっていることが明らかになりつつある [61, 62].
このように,情報熱力学は,複数の分野を横断する豊かな研究分野を形成しつつある.今後のさらなる展開に期待したい.
・沙川貴大『非平衡統計力学』 ゆらぎの熱力学から情報熱力学まで

・Maxwellのデーモンと情報熱力学
http://cat.phys.s.u-tokyo.ac.jp/publication/Suri_Kagaku_Final_Version.pdf
・はじめに:情報は物理的
・熱力学と情報
・シラードエンジン
・微小系の非平衡統計力学
・量子デーモン
・情報熱力学の第二法則
情報熱力学においては,デーモンはもはやパ ラドックスの元凶ではなく,ミクロな世界にお ける情報処理の「デバイス」としての機能を果 たす.
デーモンは情報を利用することで従来の 熱力学第二法則 (1) を破る操作も実行でき,~~~
情報熱力学は,物理学 だけでなく,情報理論や制御工学といった,様々 な分野との関連を持っている.
一般化された第 二法則 (5) は,情報と熱力学が交わる広大な世 界のごく一端を示しているに過ぎないと思われ る.
情報の物理学はまだ始まったばかりである.
・ネットワーク上の情報熱力学とその生体情報処理への応用(伊藤先生&沙川先生)
https://www.jstage.jst.go.jp/article/butsuri/72/9/72_658/_pdf
・(ベイジアン)ネットワーク上の情報熱力学
・生体シグナル伝達の情報熱力学
生体における情報の役割を明らかにすることは重要である.
近年は狭義のシステムズバイオロジーのみならず,統計物理的なアプローチの重要性が認められるようになってきている.
そのような統計物理の概念・手法に基づいた研究の流れのなかで,基礎的な熱力学に基づいた今回の研究が,新しい研究の方向への第一歩となることを期待している.
我々の研究以外でも,生体情報処理における情報熱力学の有効性が示されている.
たとえば式(7)右辺の連続極限に相当する情報流(dynamic information flow, DIF; またはlearning rate※)を用いて情報熱力学を構築し,9) 生体センサーを解析する試みがある.10)
このような,情報理論と熱力学に基づいて生物の柔軟な情報処理を理解しようとする試みは,今後さらなる展開をみせることが期待される.
※Learning rate 学習速度 ≒ 統計力学的機械学習と深く関係
〇カリフォルニア大学 数学教授 John Baez
・Information Geometry
パート 1 - 統計力学からのフィッシャー情報メトリック。
パート 2 - 統計力学アプローチをフィッシャー情報メトリックの
通常の定義に結び付けます。
パート 3 - あるシステムの混合状態へのマップを備えた
任意の多様体上のフィッシャー情報メトリック。
パート 4 - 虚数部が量子不確実性を測定する
複素数値の実数部としてのフィッシャー情報メトリック。
パート 5 - 例: 熱浴中の調和振動子。
パート 6 - 相対エントロピー。
パート 7 - 相対エントロピーの 2 次導関数の行列としての
フィッシャー情報メトリック。
パート 8 - 情報幾何学と進化: 自然選択がベイズ推論と
どのように似ているか、またそれが
相対エントロピーとどのように関連しているか。
パート 9 - 情報幾何学と進化: 複製方程式と、
成功した種が優位に立つときのエントロピーの減少。
パート 10 - 情報幾何学と進化: レプリケータ方程式の下で
エントロピーがどのように変化するか。
パート 11 - 情報幾何学と進化: 相対情報の衰退。
パート 12 - 情報幾何学と進化: 進化ゲーム理論の紹介。
パート 13 - 情報幾何学と進化: 集団が進化的に安定した状態に
近づくにつれて相対的な情報が減少する。
パート 14 - オープン マルコフ過程と最小散逸の原理。
(Blake Pollard との共同)
パート 15 - オープン マルコフ プロセスにおける
相対エントロピーの変化。(Blake Pollard との共同執筆)
パート 16 - 複製子方程式とフィッシャー情報メトリックを関連付けた、
フィッシャーの自然選択の基本定理の更新バージョン。
パート 17 - 熱力学におけるシンプレクティック幾何学と接触幾何学。
パート 18 - 確率論におけるシンプレクティック幾何学と接触幾何学。
パート 19 - 驚き(自己情報量)と運動量の類似性、および
古典力学、熱力学、確率論間の類似性の概要。
パート 20 - 統計多様体を使用して熱力学と確率論の関係を展開します。
パート 21 - ランダム変数(正規分布/ガウス分布)のリストの
期待値に対する制約の下で
エントロピーを最大化するギブス分布の基本的な特性。
日本語訳の参考は以下のとおりです。
〇統計数理研究所 松縄 規
・分布の起源 ーノンパラメトリックな統計的不確定性関係と統計基礎方程式ー
https://core.ac.uk/download/pdf/234006407.pdf
1.なぜ分布の起源なのか?
2.記号,仮定
3.ノンパラメトリックな統計的不確定性関係と統計基礎方程式
4.実対称ランダム行列の分布の特定化
5. 実対称ランダム行列の最小不確定1性分布の例
6.あとがき
母集団分布の存在を仮定するFisherの特定化の問題を見直し,
データあるいは適切な思考実験を通じて統計基礎モデルを構築する
という意味での分布の特定化の問題に取り組むための
有力な道具立となることが分かった.
このようにして得られた統計基礎モデル系の状態の変化にともなって
どう発展するかは,関連する統計的特性関数のLegendre変換を利用し,
正準パラメータ等の統計的モデルの変化を正準情報量規準を導入して
考察することができる.それについては稿を改めて議論する.
・分布の発展 ールジャンドル変換と正準情報量規準ー
1.はじめに
2.最小KL情報量(カルバックライブラー情報量・ダイバージェンス)に基づく正準分布
3.多変量分布に対する情報量不等式
4.KL情報量の下半連続性
5.Legendre変換と正準情報量規準
6.分布の逐次発展
7.あとがき
カルバックライブラー情報量を用いて、与えられた多変量統計基礎モデルが、ある一般的な条件のもとで、移動情報量最大(or内部生成情報量最小)の意味で、「最適な統計モデル」へ「発展」する可能性を、正準情報量規準の形で考察した。
このことを考察可能にしていることの一つは
「カルバックライブラー情報量が、
”負のエントロピー(相対エントロピー)”」
であることにある。
この事実は、ボルツマンにその起源を見ることができ、
現代の統計学の研究者たちも「ときに符合を誤って」言及する基本事項である。
しかしながら、この重要な関係は統計学に十分に理解されて、取り込まれていない。
この部分に主として関係する統計理論は、
最尤法(注:自由エネルギー原理や最大エントロピー原理、測地線などの変分原理や、機械学習での最適化など)と、その精緻な修正の理論展開であるが、研究の進展についれて、統計理論そのものと、関連諸科学との交流が薄れてしまったように思える。
統計学に関連する諸科学で現れる「双対問題」の解析に重要な意味をもつ、ルジャンドル変換およびプリゴジンの内部生成エントロピーの類推として、内部生成情報量が、非常に有用な役割を演じることが分かった。
なお、ルジャンドル変換は、甘利の情報幾何による統計理論にも重要な役割を演じるものとして登場している。
(注:ルジャンドル変換からシンプレクティック構造へも関連していきます)
分布の発展という課題には、熱力学的な解析手法の中での、この変換の活用を行うことも、関連諸科学との相互理解に役立つと考え、そのような近接方法を取った。
情報幾何学の理解の上に、その積極的利用を行えば、本問題に対するより系統的で理解しやすいアプローチが提案できる可能性もある。
また逆に、ここで得た知見が情報幾何の分野に新しい解釈をもたらすかもしれない。
例えば、本稿で提案した
「移動情報」と「内部生成情報」の関係は、
平坦双対な情報空間における、互いに「双対な情報量」
あるいは「情報測地線」に、
「物理的意味を付与した」
とも解釈できる。
(注:伊藤先生の維持エントロピーと過剰エントロピー生成や、エントロピー生成速度、移動エントロピー、確率密度流などとも関係しています)
本稿執筆の過程で、統計の基礎理論が、驚くほど綺麗にルジャンドル変化に乗ってくるということを実感した。
このことは逆に、統計理論が諸科学から「共通の理解」が得られる土壌を、潜在的に有しているといえよう。
様々な分野での「ランダムな要因」に起因する発展(注:確率過程、ランダム行列など)にも、本稿の結果は部分的に当てはまるかもしれない。
〇国立研究開発法人 科学技術振興機構(略称JST)
・「情報・物理・数理の共創 ~非平衡ダイナミクスの理解が見せる新たな景色~」
https://www.jst.go.jp/crds/pdf/2022/SP/CRDS-FY2022-SP-07.pdf




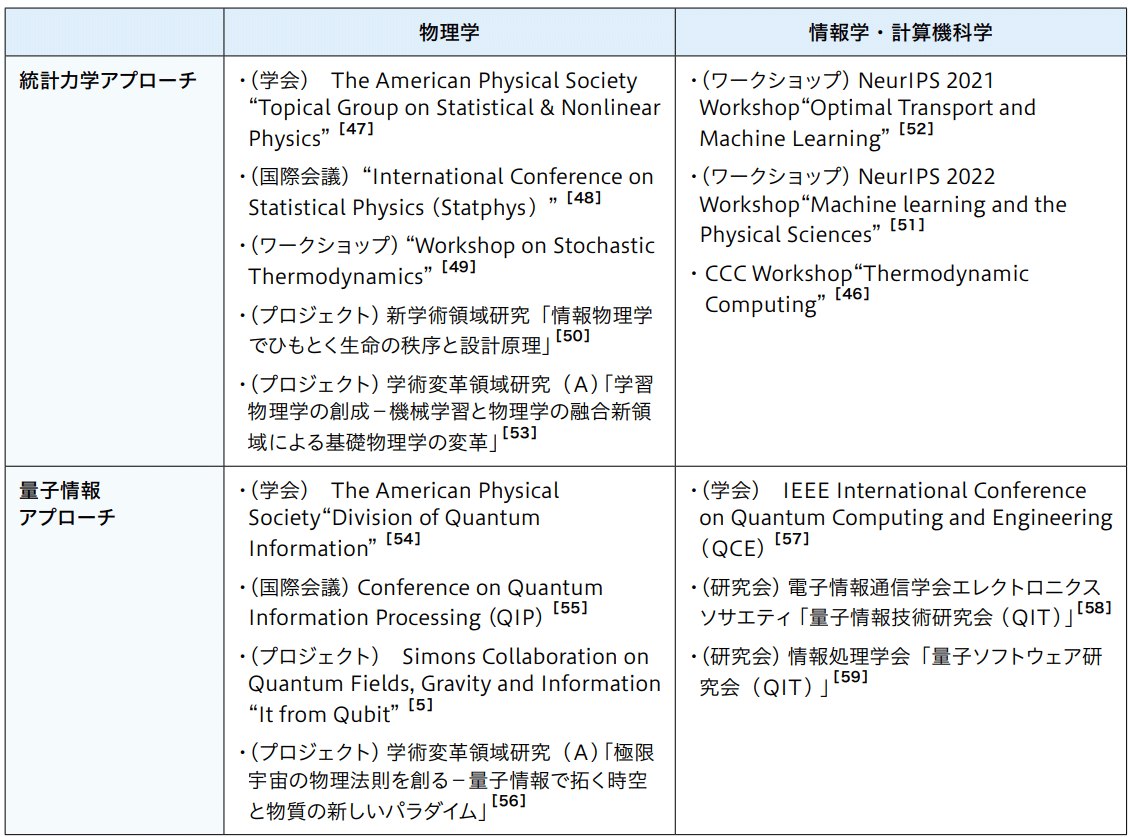

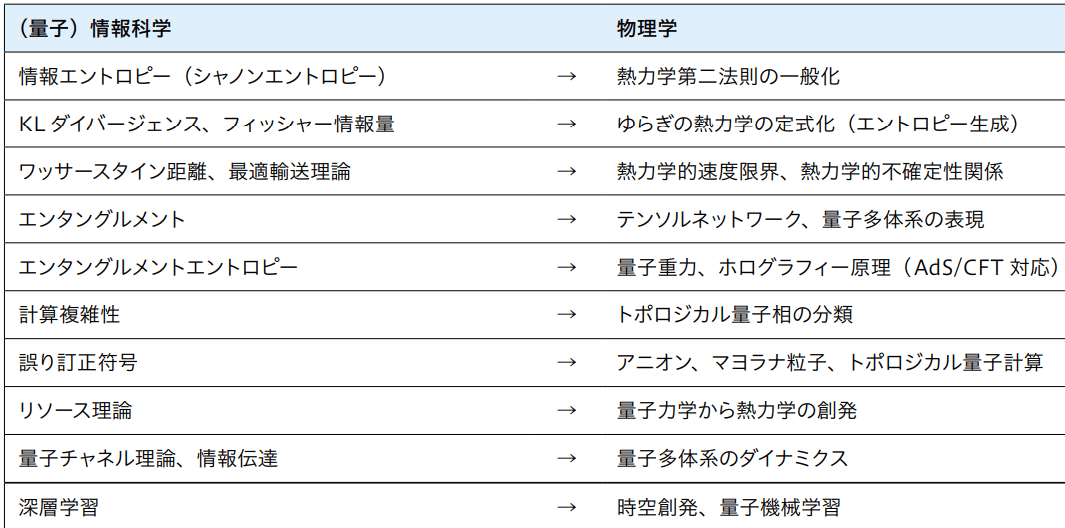




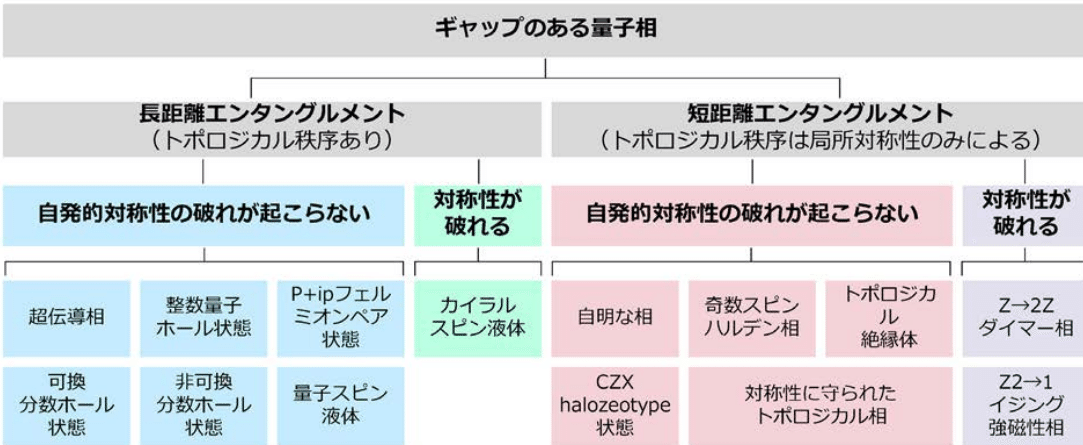
・科学技術未来戦略ワークショップ報告書:【情報と計算の物理と数理】
https://www.jst.go.jp/crds/pdf/2022/WR/CRDS-FY2022-WR-11.pdf



















〇その他
・純粋状態量子力学の量子熱力学への変質 三重大学大学院工学研究科 奥山 進治
ここでは、
Shanonn エントロピーに対して
Clausius の等式を要請することにより、
温度の類似物が導入でき、その結果、
純粋状態量子力学が量子熱力学に形式的に変質する
ことを示す。
・情報幾何学入門 ― 幾何学者から見た情報幾何学 ― 松添 博 (名古屋工業大学)
https://www.sci.kyoto-u.ac.jp/sites/default/files/2021/kce/OI9VaQ/files/170928kyoto-handout.pdf
1 多様体速習
2 統計モデルの幾何学
3 双対接続と双対平坦空間
4 最尤推定量の幾何学
・情報幾何入門 産業技術総合研究所 赤穂昭太郎
https://staff.aist.go.jp/s.akaho/papers/infogeo.pdf
共通言語としての情報幾何
• 確率モデルやその周辺分野
– 統計学
– システム制御
– 符号理論
– 最適化理論
– 統計物理
それぞれ独自の理論・アルゴリズムがあるが関係がよくわからない
情報幾何で統一的に理解しよう
・空間の構造 計量テンソル、接続・接空間、測地線
・フィッシャー情報行列(共分散行列/相関行列)、フィッシャー計量
・フィッシャー情報量、クラメールラオの情報不等式、統計的推定限界
・指数分布族と混合分布族、e接続とm接続、EMアルゴリズム
・ルジャンドル変換と双対空間、基底の変換
・部分空間、射影、カルバックライブラーダイバージェンス(カルバックライブラー情報量、発散)、拡張ピタゴラスの定理
・隠れマルコフモデル(潜在変数モデル)
・集団学習、ベイズ推定、マルコフ連鎖
・情報幾何の基礎的スタディ ~情報幾何とその応用について~
1.情報幾何とその周辺
2.情報幾何の基礎知識
(1)確率分布と幾何学その1
(2)確率分布と幾何学その2
(3)確率分布と幾何学その3
(4)確率分布について
(5)確率分布の点~座標系
(6)点の近傍~接空間・接ベクトルと自然基底
(7)点の近傍の性質~Fisher情報計量
(8)異なる点を結ぶ~アファィン接続
(9)アファィン接続その2~接続係数、平坦性と共変微分
(10)アファィン接続その3~α接続とem-接続
(11)指数型分布族その1
(12)指数型分布族その2
(13)双対接続の持つ性質
(14)ダイバージェンス
3.ニューラルネットと情報幾何
(1)ニューラルネットの統計モデルその1
(2)ニューラルネットの統計モデルその2
(3)ニューラルネットの統計モデルその3
(4)期待値パラメタと最尤推定
4.EMアルゴリズム
(1)EMアルゴリズムとは
(2)EMアルゴリズムの幾何学
(3)EMアルゴリズムの手順
・Kullback-Leibler情報量とSanovの定理
東北大学大学院理学研究科数学専攻 黒木玄 助教
https://genkuroki.github.io/documents/20160616KullbackLeibler.pdf
1.3 Kullback-Leibler 情報量と相対エントロピーの定義
1.4 Kullback-Leibler 情報量の基本性質
最大相対エントロピーの原理
1.8 Kullback-Leibler 情報量と多項分布の中心極限定理の関係
2 条件付き大数の法則からBoltzmann因子へ
4 Sanovの定理を使ったカノニカル分布の導出
4.1 分配函数とエネルギーの期待値
4.2 条件付き確率分布のカノニカル分布への収束
6 付録: Cram´erの定理
6.3 カノニカル分布の相対エントロピーとの関係
6.6 Ψ(β) = log ∑r i=1 e −βiqi の Legendre 変換は相対エントロピー
7.2 統計力学の教科書におけるカノニカル分布の導出 (1)
8 付録: 他の種類のエントロピーについて
8.1 自由エネルギーやMassieu 函数との関係
・Information geometry in quantum field theory: lessons from simple examples(情報幾何学とAdS/CFT対応、ゲージ/重力の双対性、「情報/幾何」双対性)
https://scipost.org/preprints/scipost_202002_00001v1/
こちらに日本語訳の参考があります。
1 はじめに
2 情報幾何学
3 双曲幾何学のred herring(罠)
4 不安定系の配位
7 曲率の異なる概念
8 考察
ホログラフィックRG(繰り込み群)
複雑性
・統計における幾何のかかわり 高野 嘉寿彦 自然科学教育部門 教授
2.統計多様体
共分散行列と正規分布
概複素構造をもつKähler-like 統計多様体
3.指数型分布族
5.概複素構造をもつ統計多様体
概 Hermite-like 多様体
Kähler-like 統計多様体
6.概複素構造をもつ指数型分布族の例
・大阪市立大学数学研究所ミニスクール 「情報幾何への入門と応用」
https://www.sci.osaka-cu.ac.jp/~ohnita/2006/inf_geom/sos_dan/book_0403.pdf
長岡 浩司 情報幾何の基礎概念
渡辺 澄夫 代数幾何と学習理論の関係について (1)
栗木 哲 積分幾何と統計分布理論
田中 利幸 確率モデルにもとづく推論の情報幾何 (1)
田中 勝 ゲージ変換とα-接続
高野 嘉寿彦 概複素構造をもつ統計的モデルの例について
・情報幾何と機械学習 赤穂昭太郎
https://staff.aist.go.jp/s.akaho/papers/infogeo-sice.pdf
はじめに:なぜ情報幾何なのか
図 1 機械学習の幾何的イメージ情報幾何とは何
機械学習の情報幾何
おわりに
・量子系のエンタングルメントと幾何学(ゲージ重力対応) 講師:松枝宏明(仙台高等専門学校 教授)
http://nakamura-lab.phys.sci.ehime-u.ac.jp/matsueda2018.pdf
第 3 章 エンタングルメントとテンソル積変分理論
第 4 章 ブラックホール熱力学
第 5 章 情報幾何的アプローチによるゲージ重力対応の研究
5.1 双曲的時空におけるバルク境界対応 .66
5.1.1 AdS/CFT 対応 . 66
5.1.2 GKP-Witten 関係式 .67
5.1.3 笠–高柳の公式 .69
5.2 情報幾何によるゲージ重力対応の研究 .71
5.2.1 情報幾何の基礎とエンタングルメント熱力学 . 71
5.2.2 ガウス分布の幾何学 .73
5.2.3 時空間座標とカノニカル変数の間の変換則,
エントロピー公式の導出 . 74
5.2.4 双対性とバルク境界対応 .76
・第一原理計算と密度汎関数理論(数値計算)
※関数=値の集合(リスト・ベクトル)
汎関数=関数の集合(リスト・ベクトル)
・確率分布・確率密度関数は、確率量・確率測度の集合
・確率密度汎関数は、確率分布(確率密度関数)の集合
・量子力学の経路積分 ≒ 汎関数積分 → 密度汎関数理論
・グランドカノニカル分布 → 混合分布族(異なるパラメータを持ったカノニカル分布の集合) → 汎関数
・確率密度行列の集合や、波動関数の集合 → 汎密度行列・波動汎関数 ≒ 非平衡量子統計力学(各密度行列、汎導関数に対するギブス測度の割り当て)
