
2023年本試験問題 第4問 「表計算でデータサイエンス?」

高橋尚子(國學院大學)
今回は,2023年1月に実施された大学入学共通テストの「情報関係基礎」第4問$${^{1)}}$$です.
第4問は,第3問と対で,どちらかを選択する問題で,内容は表計算ソフトウェアを使ってのデータ処理(一種のプログラミング)を扱っています.プログラミングができない人が選択するとか,たかが表計算かと袖にすることはできません.題材がとても実用的で,一度じっくり取り組んでみる価値があります.
今回の題材は住民活動の情報共有サイトです.4つのカテゴリ(清掃・植樹・防犯・観光)で構成され,活動に参加した会員が動画投稿・動画視聴・コメント投稿を行えます.このデータを使って,コメント投稿の割合が高いカテゴリや,初めて視聴される割合が高いカテゴリを見つけ出し,他のカテゴリに案内する記事を作成しようと考えます.そこで,動画投稿・コメント投稿の多い会員の動作分析を行うことにする,という流れです.問題文には、前提が書かれ、全体的に長いのが特徴ですので,まずは,この話の流れを掴むことが大事です.
また,ここでは,シート名は「太字」,セルに入力された文字列は“文字列”,式はフォントをCourierで記載しています.
【問1】
問1は,表計算ソフトのうち,条件付きセルの個数や,論理関数の複雑な条件判断の式を完成させる問題です.機能(関数)の使い方は,問題用紙の最後に説明が掲載されていますので,確認するとよいでしょう.
会員の投稿数をまとめる
動作分析の手始めとして,分析に同意した10名の会員について,7週間にわたり動画投稿回数とカテゴリごとのコメント投稿数を記録したシート1「週別履歴」を作成します.次に,それに基づき,会員ごとに7週間で,実際に行動した週数,動画投稿数,各カテゴリへのコメント投稿数を記録したシート2「会員まとめ」を作成します(図1).
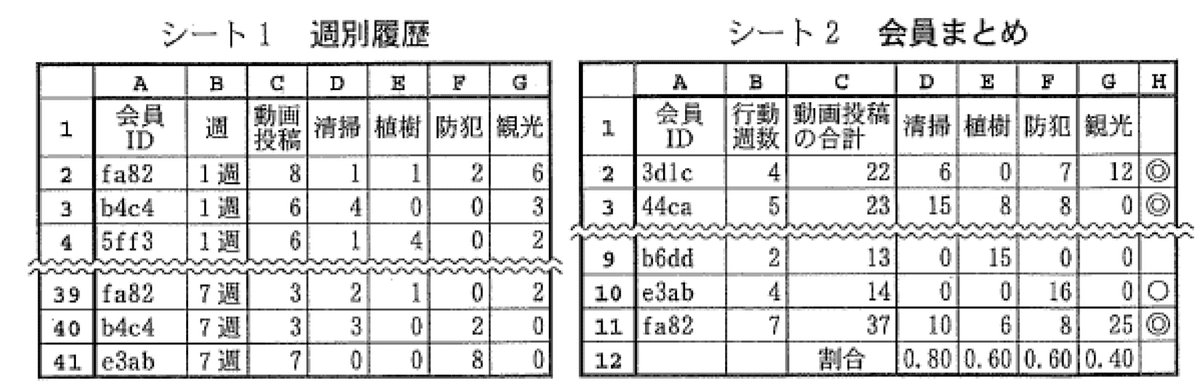
「会員まとめ」のB列“行動週数”は,「週別履歴」のA列「会員ID」ごとの出現数を合計します.そのため,検索条件がついたセルの個数を返すCOUNTIF(セル範囲,検索条件)を使います.B2に書く式【ア】は,A列と一致するセルの個数を求めるため,セル範囲を「週別履歴」の2行目から41行目と指定し,検索条件をA2とした④COUNTIF(週別履歴!A$2~A$41,A2)となります.この式は,B3〜B11に複写するため,参照するセル範囲の行番号が変わらないように指定しています.C列“動画投稿の合計”は,同じようですが,セルの値を合計するので,SUMIF(セル範囲1,検索条件,セル範囲2)を使います.C2には,SUMIF(週別履歴!【イ】,A2,週別履歴!【ウ】)と入力します.よって,セル範囲1の【イ】はA列を範囲にするので⓪A$2~A$41,セル範囲2の【ウ】はC列を範囲にするので②C$2~C$41とします.

完成したC2の式は,次のようになります。


会員の行動と投稿数を評価する
次に,「会員まとめ」にH列(判定欄)を追加して,会員の活動状況を3つに分けます.分け方は,“行動週数”が4以上かつ“動画投稿の合計”が7以上である会員について,複数カテゴリに投稿していれば◎を,そうでなければ○を,7未満の会員に対しては空白文字列を表示させるようにします.IF(検索条件,式1,式2)を使いますが,プログラミングの分岐で考えても複雑な指定です.さらに,条件が重なるので,IFの中にIFを入れる,いわゆる入れ子という形にします.フローチャートで書くと,図2のようになります.ここで,説明のために,IF(外側の条件,外側の式1,外側の式2)と,外側の式1に入れる式をIF(内側の条件,内側の式1,内側の式2)として,区別します.

IFの外側の条件は,2つの条件が「かつ」で指定されていますので,AND(条件式1,条件式2)を使います.ここで,H2には IF (AND (B2>=【エ】, C2>=【オ】), IF (COUNTIF (D2~G2,"=/0") >=2,【カ】,【キ】),【ク】) と入力します.よって,B2“行動週数”の条件【エ】は4,C2“動画投稿の合計”の条件【オ】は7,とします.外側の式1に重ねてIFを使います.内側の条件にCOUNTIFで複数カテゴリに投稿したかどうかを判断する式,セル範囲D2からG2のうち,0でない(≠0)のセル個数が2個以上と指定しています.この条件に合致する内側の式1【カ】は②”◎”,合致しない内側の式2【キ】は①”〇”,そして外側の式2【ク】は⓪””,とします.
完成したH2の式は,次のようになります.


最後に「会員まとめ」の12行目の4つのカテゴリ欄に,そのカテゴリにコメント投稿した人数の割合を求めます.コメントを1個以上投稿したセルの個数をCOUNTIFを使って求め,10名で割る式を作ります.よって,COUNTIFの検索条件は1以上ですから,【ケ】は1とします.
【問2】
問2は,条件判断を選択する問題と,2つのシートから特徴を見つける問題です.
まず,「会員まとめ」で◎のついた会員だけを対象に,動画視聴を始めてから対象カテゴリを移動した履歴をダウンロードして,シート3「カテゴリ移動」を作成します(図3).ダウンロードしたデータは250件以上あり,途中が省略されています.

カテゴリの移動を一覧できる表にする
A列には移動前のカテゴリの名前を,B列には移動後のカテゴリの名前が記録されています.一連の視聴履歴の始まりは“(始)”として記録し,最後に視聴した記録の移動先は“(終)”と記録されています.新たに,C列に“(始)”,D列からG列までに各カテゴリ名の列を追加して,移動前カテゴリを列方向に,移動後カテゴリを行方向として,移動前カテゴリの列位置に移動後のカテゴリ名を入力し,それ以外の列位置には“-”を設定します.一目でカテゴリの移動が分かるような表を作ります.
つまりカテゴリを移動したセルだけに,移動後のカテゴリ名が入力されるようC3にIFを使って式を作ります.作成した式は,行方向と列方向の両方に複写するため,セル参照を変更するかどうかに注意が必要です.移動前のA列,移動後のB列,移動前カテゴリの2行目は変更しないように指定します.C2にはIF (【コ】= 【サ】, 【シ】, ”-” ) と入力します.よって,条件の左辺【コ】と右辺【サ】は順不同で①$A3と⑧C$2,式1【シ】は④$B3,とします.
完成したC3の式は,次のようになります.

続いて,「カテゴリ移動」から,列方向に“(始)”と移動前カテゴリを,行方向に移動後カテゴリと“(終)”を並べ,それぞれの位置にその移動前・移動後の移動の回数を計算したシート4「移動回数」を作ります(図4の左).回数の計算は,カテゴリ名に合致するセルの個数を求めるので,COUNTIFを使います.C3には COUNTIF(カテゴリ移動!【ス】,【セ】 )と入力します.よって,セル範囲【ス】は「カテゴリ移動」の ⑤C$3~C$253,検索条件【セ】は④$B3,とします.作成した式は,D3~G253まで複写するため,検索するセル範囲は行を変更しない,検索条件は列を変更しないように指定します.
完成したC3の式は,次のようになります.



カテゴリの移動回数と割合を比較する
さらに,シート4「移動回数」から,それぞれの移動前カテゴリから移動後カテゴリへの移動の割合を求めたシート5「移動割合」を作ります(図4の右).

このシートの式は問われていません.最後に,2つのシート「移動回数」・「移動割合」から,読み取れる特徴を見つけます.選択肢⓪は「移動割合」のD列を見ると観光でなく植樹が多いので違います.①は「移動割合」の4行目を見ると防犯でなく清掃が多いので違います.②は「移動回数」のD4とE5,および「移動割合」のD4とE5を比較すると合致します.③は「移動回数」のD4とE5を比較すると合致しません.よって【ソ】は②が把握できます.

【問3】
問3は最終目的である分析結果を求めるため,条件判断の選択やセル探索の設定,カテゴリ移動の流れ図を完成させる問題です.
「移動割合」を使って,移動前カテゴリから移動する先の多い順に1,2,…と順位をつけるシート6「移動順位」を作成します(図5).

カテゴリごとの移動順位を表にする
この「移動割合」から「移動順位」を,IFとRANK(式,セル範囲)を使って求めます.C3にはIF(【タ】,”-”,RANK(移動割合!C3,移動割合!【チ】)と入力します.よって,IFの条件式は,移動前カテゴリ(列)ごとに,移動前と移動後が同じ(移動してない)場合なので,【タ】は①$B3=C$2,とします.合致しない(移動した)場合の式2はRANKを使い,セル範囲【チ】は①C$3~C$7,とします.これで式を右に複写したときに列は変更しますが,下に複写しても行は変更しません.ここは,選択する解答群が入り組んでいるので,落ち着いて探しましょう.
完成したC3の式は,次のようになります.




カテゴリの移動順位を確定する
これら複数のシート結果をまとめてシート7「分析一覧」を作成しています(図6).
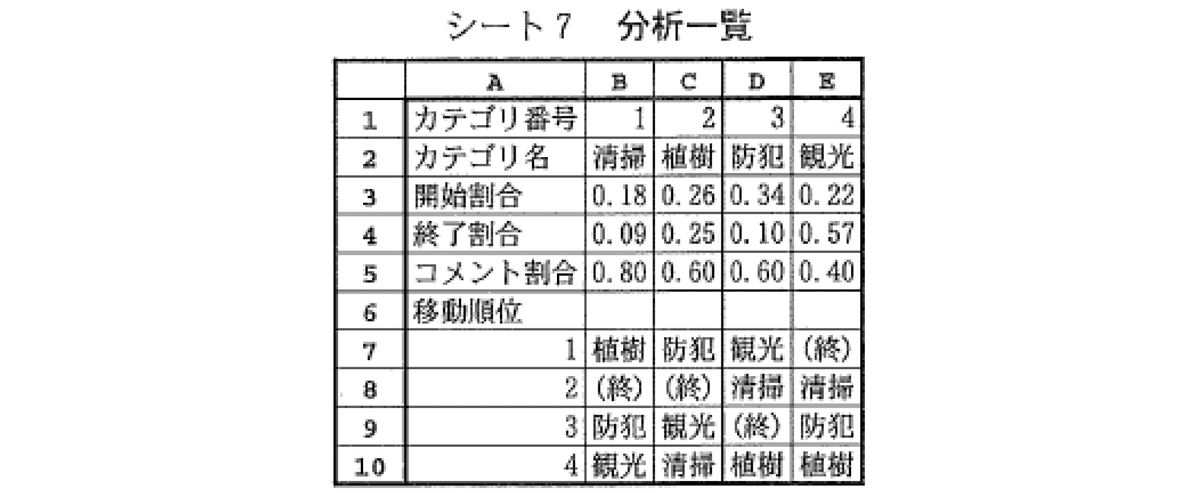
5行目までは,それぞれのカテゴリについて,視聴を開始する割合,視聴が終了する割合,コメントを投稿した会員の割合を並べてあります.6行目からは,カテゴリから次に移動する先のカテゴリを,移動順位に従って並べるための数式をVLOOKUP(検索値,セル範囲,列位置)を使って求めます.B7にはVLOOKUP(【ツ】,移動順位!【テ】,6-【ト】)と入力します.よって,検索値【ツ】は⓪$A7,セル範囲【テ】は⑨D$3~$H$7,6から引く列位置【ト】は①B$1,とします.この式を,B8~B10とC7~E10に複写しますが,セル範囲と列位置は右に複写したとき列が変更するようになります.列位置を6からカテゴリ番号を引いているのは,「移動割合」のH列を参照しているからです.
ここも,選択する解答群がシート6といっしょになっているので,該当する記号に合わせて探しましょう.
完成したB7の式は,次のようになります.

カテゴリの移動を矢印でつないだ図にする
最後は,「分析一覧」を使って,カテゴリのつながり図を作ります.図7の左は,コメントを投稿した割合が最も高いカテゴリ清掃(B2)から移動順位1位のカテゴリのつながりです.移動順位1位であるカテゴリを拾うと,【ナ】【ニ】【ヌ】はそれぞれ②植樹(B7),③防犯(C7),④観光(D7),となります(図7の左).
図7の右は,開始割合が最も高いカテゴリ防犯(D2)から移動順位が“(終)”より上位になるカテゴリのつながりです.【ネ】は④観光(D7)となり,観光からの移動順位1位が“(終)”なので先がありません.次に,【ノ】は①清掃(D8),【ハ】は②植樹(B7)となり,防犯(C7)に戻ります(図7の右).


最後の移動図から,コメント投稿の割合が高いカテゴリや,初めて視聴される割合が高いカテゴリは,「清掃」や「防犯」であるということが分かりました.が,それについての評価などは行っていません.
【問題を通して】
ダウンロードしたデータを使用するなど,データサイエンスやビックデータを意識した問題のように見えます.また,データ数が多いので,問題用紙にすべての具体例がない表は,力業(ちからわざ)では解答できません.逆に,問2の後半から問3にかけては,具体例が表にすべて示されているので,そのことに気がつけば,問2の前半まで,式が分からなくても答えられます.問題の導入部分を丁寧に作り込み,後半はササッと流した感じです.そのわりに,解答群が入り組んでいたり,複数回使用できたりと,それぞれに確認が必要です.新しい「情報I」の出題を予測するような気がしないでもないです.
また,表計算ソフトの出題は,全体的に条件の設定が多く,複写を前提とした式の作成ばかりで,どれも難問です.プログラミングと同じく,表計算で実際にシート作成や関数の設定を行った経験がないと解答に時間がかかりそうです.
★なお,本稿で題材にした「情報関係基礎」の問題は,本来は専門高校の生徒を対象に想定しています.2025年に実施される共通テストの「情報I」については,下記の参考文献2)3)を参照してください.
参考文献
1)情報関係基礎アーカイブ,
https://sites.google.com/a.ipsj.or.jp/ipsjjn/resources/JHK
2)水野修治:令和7年度大学入学共通テスト『情報I』の実施に向けて ~問題作成方針に関する検討の方向性と試作問題~,情報処理, Vol.64, No.2, pp.74-77 (Feb. 2023).
https://doi.org/10.20729/00223448
3)植原啓介:大学入試センター「試作問題」の分析,情報処理,Vol.64, No.4, pp.e45-e58 (Apr. 2023).
https://note.com/ipsj/n/ne5b8f55f5346
(2023年8月12日受付)
(2023年9月5日note公開)
■高橋尚子(正会員)
本会教育および会誌担当理事を歴任(2019年~ 2023年).大学時代に女子大初のマイコンクラブを結成.女性SE第一期生として富士通入社,その後ASCIIでビジネスパソコンスクール開校,OAインストラクタを経て独立.1995年から大学で非常勤講師を始め,2007年から國學院大學経済学部で情報教育に就く.
情報処理学会ジュニア会員へのお誘い
小中高校生,高専生本科~専攻科1年,大学学部1~3年生の皆さんは,情報処理学会に無料で入会できます.会員になると有料記事の閲覧,情報処理を学べるさまざまなイベントにお得に参加できる等のメリットがあります.ぜひ,入会をご検討ください.入会はこちらから!
