
現代の社会問題の起源とその解決策〜社会物理学による考察〜
このノートについて
そもそも,社会で騒がれる数多くの問題に共通する起源は何なのか.
社会物理学という分野を通してこの考察をしてみる.
そして,現代社会にとって,現代の人間にとって,何が大事なのか?
そんなことに,ここでは想いを馳せたい.
作成から投稿までのスピード重視で書いた適当なノートなので,とにかく学んで,考えて,感じたことも含めて書かせてもらっている.何か勘違いなどもあるかもしれない.
自分なりにデータ収集や,グラフのプロット,さらに,数理モデルのシミュレーションについては追計算なども行ったので,内容が長くなってしまった.本来ならば複数のノートに分けて書いた方が良かったのかもしれないが,ご容赦願いたい.また本ノートには間違いが含まれている可能性があるため,情報を扱う際には自身でよく確認してから扱ってほしい.もちろん誤りがあり,もし親切にご指摘いただけるのなら修正するつもりである.
社会物理学(Sociophysics)とは?
21世紀に入ってから,学問の発展とともに,社会物理学(Sociophysics)はかなり発展してきている.
この分野は簡潔に言えば,物理学,主に統計力学の知識を用いて,
ミクロな個人の行動やルールから,マクロな社会の普遍的法則を導き出そうとする取り組みである.
この分野について,現在の大まか状況をいくつかのレビュー論文や,教科書を読み,学ぶ中で,私個人が考えたこと,問うたこと,その中でも特に本質的に現代社会にとって大事と感じた部分について,このノートを通して書き残せたらと思う.
どのような社会問題があるだろうか?
まず,最近のニュースで気になったものをいくつか挙げよう.
代表例:子供と教育,学校,大学の問題
人々の考え方は教育に大きく依存する.
社会は人々が作り,人々の思考によって,構成される.
特に幼少期の環境による教育は社会基盤であることは間違いない.
そこで,これからの社会の将来に大きく影響を及ぼす,子供の問題について,まずは考えたい.
子供の不登校数が過去1番の数,割合になったそうだ.
原因は,いじめの増加や,勉強が詰め込みばかりでつまらない,将来への不安など多岐にわたるようだ.この根本要因は何だろうか?
https://spc3.net/wp-content/uploads/2018/06/SR.pdf
私はこの根本要因として,現教育環境が受験といった同一レール上の競争に基づいていることが大きな問題であると感じる.インターネットなどの情報化が進み,さらにAIが発展してきた中で,そのような学校の在り方に問題があるのだと感じる(多くの大人はインターネットやゲーム,AIなどのテクノロジーが悪いと捉える場合が多いが,そもそも現在の学校が産業革命に合わせた機械を扱える人,特に工場労働者を増やすために作られたものではなかったか?).
学校を受験勉強する場(特に,同年代の子供達を同じレール上でレースさせる場,教員から一方的な教育を受ける場)ではなくて,社会的な交流と創造の場としての在り方への大きなシフトが必要なのではないかと感じる(現在もこれを掲げてはいるが,ほとんど実践できていないと思う).
例えば,以下の文献がそのことを大きく取り上げている(能力主義,メリトクラシーへの批判).特に,お互いに大人から子供まで広く,双方向に学び合い,問いあって,創造する場としての学校や大学が必要なのかもしれないと感じる.
また,由々しき問題として,大学のビジネス化,さらにそこに追従するように高校までのカリキュラムの構成があるだろう.
大学が法人化され,大学内で収入を確保する必要が大きくなったと同時に,少子化が追い打ちをかけ,子供達やその家族から大きくお金をまるで搾取するシステムになってしまった.学生が学校や大学を卒業する頃には,多額の借金を抱えていて,それらを安定して返せるほど安定した仕事もない,ようやく返し終わる頃には結婚適齢期もすぎるというような,ある種のトラップまで生まれている.その機能不全の割に,皆が大学へ行くから行くというようになり,大学進学率は年々上昇し,もはや年ごとの大卒率は過半数を超え,当たり前になっている.そして何より,同じ学部に入れば,皆ほとんど同じことを学んでいて,オリジナリティが学部ではもちろん,個人でもほとんど全くない.個人のオリジナリティやキャラクターを作るのは完全に個人任せですべて自己責任となっている.むしろその活動の邪魔なタスクとして授業や講義が存在しうる場合すらある.これでは何のための学歴であり,学びなのか全くわからないし,機械的なレールに乗せて,はみ出ることを許さない.まるで,罪人,囚人のように扱っていて,人を不幸にしているだけだろう.これはその延長である,大学院に行っても同じことだし,ほとんどの研究者もあらゆるすでに用意された評価指標の中で生きている.これは企業も同様であろう.
そして,多様性が問題になり,それとまるで相反するような,女性限定などのフェミニズム的な募集や,産学連携重視や,資格,即戦力重視の,まるで多様性が無い募集が増えるという矛盾を抱えるわけである.これはとても滑稽で,もはやお笑いじゃないかとさえ感じる.
(ここで、女性限定募集はわかりやすいので補足させていただきたい。少なくとも私の知る限り、多くのまともな女性にとって、このような募集は余計なお世話で、採用後に”女性だから〜”などの嫌味を言われるであろうと言う心理的負担や、偏った男性中心の思考環境下に呆れて避ける傾向が多い。つまり、このような募集は、現在の男性偏向の職場をさらに助長し、悪化させていくと言える。まるで全く相手の立場に立って考えることのできていない、想像し難いほど上から目線の、一方的かつ、短絡的な偏見に満ちた悪質なものである。それは誰も得しない、極めて害悪な募集方針なので、徹底的に批判させていただいた。)
これは日本に限った問題ではない.
全世界が,テクノロジーの進展に合わせた価値観が何かわからなくなって,古い教育システムからの更新がうまくできていない.
入試システムを変えてみたり,カリキュラムを変えてみたり,多くが試行錯誤をしている.そのため,上記と同様の問題が多くの国で見られる(実際は,他の要因とも複合的に絡み合っているだろうが…).
ただ,子供だから学校へといった概念や,教師と生徒という立場という根本を覆し,大人も子供も年齢や立場を超えて,皆互いに学び,交流し,創造し合うためにその場所に行こう,というモデルはほとんど私は知らない(静かな図書館と,大学の飛び級くらい?スポーツや,ボードゲームなども可能性があるかもしれない,最後に触れるオンラインサロンなどもあるかもしれないが,これもまだ特定の有名人のファンクラブに近い状況だろう).
よりグローバルな社会問題
個人的に一番の問題だと感じている社会問題を最初に取り上げたが,
社会問題としてあげられるのはもちろん他にもたくさんある.
よくある社会問題として,現在や将来的なものまで広く含めれば,以下のようなテーマが取り上げられている:
・少子化
・高齢化
・格差と分断
・水不足,食料不足(特にタンパク質),エネルギー不足
・環境問題(地球温暖化,森林伐採,地球環境や生物多様性の破壊,薬品汚染やマイクロプラスチック汚染など)
これらの内容は,よく政治の場でも政策として取り上げられていると思う.
また,世界的には,SDGsなどでも関連する内容は多く取り上げられている問題であろう.人類史的にも,急にこのような問題が取り上げられるようになった理由が何かあるのではないか?これらに共通する起源は何かを社会物理学を学ぶ中で自分なりに見えてきたことを書き残してみたいと思う.
ここでは,数理モデルの詳細,特に,数式の扱いや,細かな発展に関してはあえて触れずに,説明する上で重要と思われる仮定や結果,結論だけを取り上げる.詳細が気になる方はこのノート最後の参考文献をあたってほしい.ここでは,主なモデルの仮定と結果,その結論から,私なりに読み取った社会問題の起源と,その改善策について考えたことを書かせていただいた.
社会のモデル化と考察
ここでは,先に挙げた,グローバルな社会問題に関して,社会物理学の知見を引き出しながら議論してみたい.
少子化(高齢化),人口問題
まずは,人口問題についての普遍性,スケーリング則を取り上げよう.
あらゆる都市や組織,さらには,細菌などの成長で見られるスケーリング則である,Zipf's law (ジップ則,時にパレート・ジップ則)について紹介する.
*Zipf's law
(ジップ則,特に,都市のサイズと人口成長の普遍性では,rank-size rule)
人口が順位$${r}$$位の人口を$${P_r}$$とした時,第1位の人口$${P_1}$$を使って,
$${P_r = P_1 n^{-\alpha}}$$($${\alpha \sim 1}$$)
が成り立つ.(実際のジップ則はこれをより一般的に拡張したもの.)
このスケーリング則は都市や,国単位など,ある程度規模の大きい集まりになると成立しているようだ.
以下の日本の都市データを利用して,プロットしてみよう.

指数$${\alpha \sim 0.83}$$という結果が得られた.
このように日本の都市においても,Zipf’s law が成り立っていることがわかる.
どのような人々の行動によって,このスケーリングが成り立っているのか,スケーリング則のミクロな起源を知りたいと思うのは自然な考えだろう.
人々のランダムな振る舞い(空いている近隣スペースへと広がろうとする感じ)のモデル(専門的には,ランダム成長モデル)や,
人々が作るつながりのネットワークを模擬したモデル(バラバシ・アルバートモデル,これは以下で議論したい)
から,類似の結果を得られることが知られているが,
結局,ミクロな相互作用から,このマクロなスケーリング則(Zipf’s law)の導出にはまだまだ議論の余地が多いようだ[Saichev et al., 2009].
このスケーリング則は,人間の具体的な戦略行動によらずに,生物としてのランダムな選択が招いた,単純な自然現象によるものと言えるかもしれない.そのため,この法則によるものかわからないが,ブラックホール型自治体と言われるように,地方から,一部の都市圏へと,若年層を中心に,より多様な就職先や,キャリアを求めて,人口吸引が起こっていることが地方の人口不足を引き起こしていると問題視され,多くの自治体が消滅する可能性が議論されているのが現状だ.
ブラックホール型自治体が出現してしまう原因として,魅力的な就職先がない問題だとか,地方に魅力がないからなどが取り上げられているが,この問題の実の原因は,単純な自然現象,ランダム成長とネットワークの成長の関係に人類,日本がついていけていないだけでなのかもしれない.
言い換えれば,これは人口が増えていけば起きて当たり前の現象であり,もはや政策等で対処しても無駄なのかもしれない.人口問題に逆らわずに,これが起こる前提で個人レベルや,社会レベルでサポートし合うシステムを作るのが大事なのかもしれない.
格差と分断,対立,官僚化の起源
ここでは,格差や対立がどのような起源で起こるのか,
また,そこから生じる,官僚化,ピラミッド構造組織の発生の起源に,
社会物理学の知見から迫っていきたいと思う.
*segregation model (棲み分けモデル,分断のモデル)
まずは分断モデルを作ってみよう.
2次元の正方格子 16x16 マスのシステムを考えてみる.
各格子点上にランダムに2種類の点,
A(赤)とB(青)を50%と50%の割合で配置する.
(点の数は全マス16x16に対しての割合,密度でユーザーが与えている.)
ここで,各点から隣接するマスを考えよう.
異種同士,AとBが隣接する場合には確率 $${p_{AB}}$$ で別の空いているマスへ移動するとする.
また,同種粒子が隣接するマスにいるときは確率$${p}$$で別のマスへ移動を行う.
異種同士は居心地が悪いとして,常に$${p_{ab} > p}$$ であるとする.
ステップごとに,この操作を行う.
すると,以下のような結果が得られる.

このモデルの面白い点は,
異種に囲まれた点は居心地が悪く,移動していく
というメカニズムを入れただけだが,
そのようにすると,同種同士が自然と集まりだす.
これで,所謂,分断ができあがります.
つまり,異なる思想を持っていて,そのような人たちに囲まれて居心地が悪く,移動し合っていくにつれ,自然と似たもの同士が集まり,似たもの同士が異なる思想を持つ集団を敵対し合う,そんなことが起こり得るわけです.
しかし,移動する確率はもちろん,密度を変えれば以下のようになります.

このようにすると,青と赤のクラスターが先ほどよりも小さくなり,互いに混じり合っていて,分断が起こりにくくなっているのがわかる.
つまり,密度を下げれば,分断が解消される可能性があると考えられる.
(もちろん,定量的にどのくらい分断している,もしくは解消されていると言えるか,さらに検討する余地はあるが…)
*Bonabeau model (ボナボーモデル,格差と官僚化のモデル)
次に,格差と官僚化が生じるメカニズムについてのモデルを扱いたいと思う.このモデルは Ising モデルから着想されたモデルである.格差が生じる理由を密度による相転移現象から理解することができる.さらに,このモデルは Ising モデルベースで構築されていて,平均場近似による解析が可能であるなど,現象の本質を理解する上で便利なモデルになっている[Bonabeau et al., 1995].
・モデルの設定
以下にどのようなモデルなのか簡単に説明しよう.
2D-square lattice を考えよう.サイズを$${L \times L}$$とする.
ここではスピンではなく,格子点上に粒子(粒子数$${N}$$)をランダムに配置する.各粒子はステップごとに隣接する格子点のいずれかにランダムに進む(ランダムウォーク).
同じ点に配置された粒子同士は戦闘する.$${i}$$番目の粒子が$${j}$$番目の粒子に勝つ確率$${Q_{ij}^{+}}$$は以下の式に従う:
$${Q_{ij}^{+} = 1/(1 + \exp(-\eta \Delta_{ij})), \Delta_{ij} = F_i - F_j}$$
ここで,$${\eta}$$ は熱揺らぎの大きさに相当するパラメタであり,戦闘結果のランダムさを与える.
$${F_i}$$ は粒子の強さを表しており,$${F_i}$$ はランダムに初期値を与える. $${F_i}$$ は以下のように各ステップごとに緩和する:
$${F_i \to F_i - \mu \tanh(F_i)}$$
$${\mu}$$ は緩和パラメタ(忘却パラメタ)とする. また,各粒子について,戦闘に勝利した場合には,$${+1}$$,敗北した場合には,$${-1}$$を粒子の強さ$${F}$$に加える.

・シミュレーションと結果
シミュレーションはモンテカルロ(Monte Carlo)法で行う.
技術的だが,一応詳細として,モンテカルロ法の平衡ステップは$${T_{eq} = 5 \times 10^4}$$, モンテカルロステップは$${T_{mc} = 1 \times 10^4}$$としている.また,モンテカルロ法でのメリットは粒子数によってほぼ計算量が確定していることであり,密度変更がしやすいことなどがある(計算量は$${\mathcal{O}(N^2)}$$).
シミュレーションパラメタは$${N = 1000, \mu = 0.1, \eta = 5}$$ として,シミュレーション結果を示そう.
ユーザーが指定した数の粒子数(ここでは15個)を全粒子数の中からランダムに注目し.その粒子の瞬間平均勝率$${\braket{P_{i}}}$$の時間変化を並べて1つのグラフに3次元プロットしている(各軸は各粒子のラベル,時間,瞬間平均勝率である).
粒子の瞬間的な勝率$${\braket{P_{i}}}$$は以下のように定義する:
$${ \braket{P_{i}} = \frac{1}{N-1} \sum_{j = 1, j \neq i}^{N} \frac{1}{1 + e^{-\eta \Delta_{ij}}} }$$
密度$${\rho=0.1, 10}$$の2つの状況を見てみよう.


また, オーダーパラメタとして,ここでは,粒子の勝率の揺らぎを用いる.この揺らぎが大きいほど,実力(強さ)の格差が大きくなっていることを意味する.オーダーパラメタの計算方法は生物学的アナロジーを利用して,以下のように行っている:
$${i}$$番目の粒子のそのステップまでの勝利数$${D_i}$$(Dominance) と敗北数 $${S_i}$$(Subordinations) として,$${i}$$番目の粒子の瞬間的な勝利確率 $${X_i = D_i / (D_i + S_i)}$$を用いて,$${\sigma^2 = \sum_{i=1}^{N} (X_i - 0.5)^2}$$ を定義する.
オーダーパラメタはこの値を用いた粒子平均$${\sigma^2 / N}$$ より計算している.
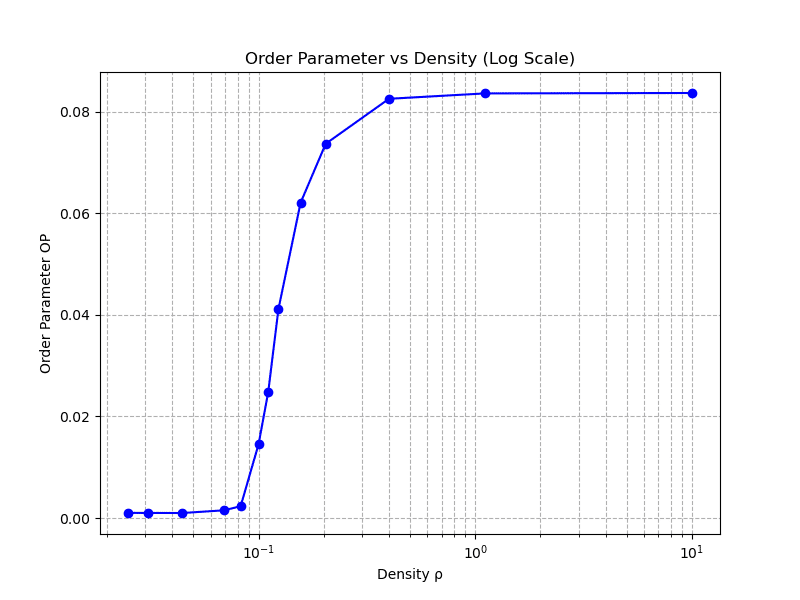
ここで重要なのは,人口密度がある密度(臨界密度)を超えた時に,急激に平等社会から格差社会への移行(転移)が起こっているということだ.
以降では,転移が起こる臨界密度はこのモデルのどんなパラメタによって決まるのかを議論していこう.
・平均場近似による解析
このモデルの最大のメリットとも言える.平均場近似による解析を少しだけ紹介する(詳細は煩雑なので,直接文献を参照のこと).この解析によって,どのような条件で平等主義社会から格差社会への転移が起こっているのかのヒントが明瞭に得られる.
このモデルの時間発展式は以下のように記述される:
$${\frac{dD_i}{dt} = \frac{\rho}{N} \sum_{j =1, j \neq i}^{N} Q_{ij}^{+}}$$
$${\frac{dS_i}{dt} = \frac{\rho}{N} \sum_{j =1, j \neq i}^{N} Q_{ij}^{-}}$$
$${\frac{dF_i}{dt} = \frac{dD_i}{dt} - \frac{dS_i}{dt} - \mu g(F_i)}$$
ここで,$${Q_{ij}^{-} = 1 - Q_{ij}^{+}}$$である.
$${g(F_i) = \tanh{F_i}}$$は忘却関数として定義している.
この微分方程式の安定性解析を行うと,以下の平均場解析に臨界密度$${\rho_c}$$が得られる(Monte Carlo シミュレーションとはずれるが,変数への依存性は同じ):
$${\rho_{c} = \frac{2\mu}{\eta (1 + \frac{1}{N})} \sim \frac{2 \mu}{\eta}}$$
where, $${N \gg 1}$$
この結果より,格差社会への転移点は,忘却度$${\mu}$$とノイズの大きさ$${\eta}$$($${1/\eta}$$が大きいほど,ノイズが大きいことを意味することに注意)によって依存し,
$${\rho_{c}(\eta, \mu) = 2\mu/\eta}$$
のように与えられる.
つまり,現在のように人口密度が大きい社会では,戦闘におけるノイズを大きくするか,以前の戦闘(成果や経験)を重視しない社会によって,より平等な社会に移行することができることを意味する.ただし,このモデルから,格差がない状態は全員が揺らいでいて,ある種の不安定ともいえる.むしろ,社会秩序には多少の格差がないといけないのかもしれません.(各々がちょうど良い強さを手に入れた結果,格差がある状態?)
社会ネットワーク:人々はどのように繋がっているのか?
人々のつながりは大事だ,しかしテレビ番組などを見ていてわかるように,いつも大体同じ人が出演したり,活躍している.それは人々のつながりの中で一部のコミュニティが目立った活躍をしているだけとも言える.
人々の社会の構造の持つ性質はなんだろうか?
そんなことを考えるためにグラフ理論を基礎として,ネットワークの持つ普遍性を探ってみよう.
*ネットワーク(グラフ理論)の基礎知識
まずはネットワークの構造を理解するにあたって,グラフ理論をベースとするため,グラフ理論の基礎知識を簡単に示しておく.

・ノードとリンク
ネットワークは「ノード」と「リンク」の繋がりによって表される.
どのようなものをノードやリンクに定義するかは状況によって異なる.
例えば,ソーシャルメディアのネットワークを考えると,ノードは人が持つスマートフォンなどのデバイス,リンクはデバイス同士を繋げる通信網といったように考えることができる.

・次数と平均次数
各ノードに対して,つながったリンクの数を「次数(degree)」という.
ネットワークの持つ平均次数は以下のように計算される:
$${\braket{k} = \frac{1}{2N} \sum_{i = 1}^{N} k_{i}}$$
ここで,$${N}$$はネットワーク内の全てのノード数であり,$${k_{i}}$$は$${i}$$番目のノードの次数である.

・平均経路長
ネットワーク内の$${i}$$と$${j}$$番目のノードを繋ぐリンク数の最小を$${d_{ij}}$$として,その全ての組み合わせを計算し,平均をとったものを「平均経路長」という:
$${\braket{d} = \frac{1}{N(N-1)} \sum_{i,j=1,\cdots,N / i \neq j} d_{ij} }$$
この計算は「幅優先探索」などのアルゴリズムを用いて,計算するのが一般的である.
以後の議論では,この平均経路長に関するスケーリング則を与える(スモールワールド性).
・クラスター係数
あるノード$${i}$$に着目して,そのノードと1つのリンクだけを介してつながる距離1のノードを考える.距離1のノード同士が1つリンクでつながっていて,ノード$${i}$$を含めて三角関係を作っている場合に,クラスターと呼ぶ.
局所クラスター係数は,$${i}$$番目のノードにつながったノード同士を繋ぐリンク数$${L_i}$$(クラスターの個数とも言える)および次数$${k_i}$$を用いて,
$${C_i = \frac{L_i}{{}_{k_i}C_{2}} = \frac{2L_i}{k_i (k_i - 1)} }$$
のように計算される.
平均クラスター係数は全てのノードについて,局所クラスター係数を計算し,全ノードでの平均
$${\braket{C} = \frac{1}{N} \sum_{i = 1}^{N} C_i }$$
のように計算される.

以上で,これから説明するネットワークの持つ性質を議論できる準備が整った.
・small-world(スモールワールド)
これは,「6次の隔たり」と言われ,有名な話である.
あなたの友達の友達の友達の…というように,6人を介すれば,世界中の誰にでもつながることができると言われる話である.
(現在ではインターネットなどつながりの発達によって,3次や4次などとも言われるほどになっている.)
あるネットワークがあるとき,何次の隔たりなのかを調べる方法を考えてみよう.
平均次数 $${\braket{k}}$$ のネットワークを考える.
ネットワーク内の1つのノードには,平均次数 $${\braket{k}}$$ より,平均$${\braket{k}}$$個のノードがリンクによって接続されている.
1つのノードにつながった,$${\braket{k}}$$個のノードのうちの1つについても,平均$${\braket{k}}$$個のノードがつながっている.
この議論を用いれば,ネットワーク内の1つのノードについて,
1つのリンクでつながる平均のノード数は,$${\braket{k}}$$
2つのリンクを介してつながる平均のノード数は,$${\braket{k}^2}$$
3つのリンクを介してつながる平均のノード数は,$${\braket{k}^3}$$
…
のように考えられる(ランダムネットワークの仮定).
これより,平均経路長$${\braket{d}}$$を用いて,
$${N \sim 1 + \braket{k} + \braket{k}^2 + \braket{k}^3 + \cdots \sim \braket{k}^{\braket{d}}}$$
のように近似できる.
よって,平均経路長$${\braket{d}}$$に関するスケーリング則が得られる:
$${\braket{d} \sim \frac{\ln{N}}{\ln{k}}}$$
スモールの意味は,ネットワーク内の2つのノードを繋ぐ平均経路長$${\braket{d}}$$がノードの総数$${N}$$に対して,たかだか$${\ln{N}}$$にしか依存しないことを意味する.
例えば,同じ平均次数を持つネットワークを考えた時,
ノードの総数が$${N=10^6}$$(100万)のネットワークと,$${N=10^{12}}$$ (1兆)のネットワークで,平均経路長がやっと2倍になる程度の差しかない.
その割に平均次数$${\braket{k}}$$に対しては,大きな変動がある.
例えば,あなたのスマートフォンにはSNSなどを通してどれだけの人とつながっているだろうか?
人にもよるだろうが,全てのサービスでのつながりをトータルすれば,$${\braket{k} \sim 10^3}$$人程度とされることが多い.
ここで,地球の全人口を80億人 ($${N \sim 8 \times 10^9}$$) とすれば,隔たりの次数は,
$${\braket{d} \sim \frac{\ln{(8 \times 10^9)}}{\ln{(10^3)}} \sim 3.3}$$
という結果が得られる.
我々はたった3人を介すだけであらゆる人とつながっている.
あなたの友達の友達の友達くらいで世界中の人とつながっていることになる.
これはあなたにとって信じられる結果だろうか?
私はこの結果を通して,いかに周りの人を大切にするだけで世界が変わるかを考えるきっかけになればと思う.極端な話だが,あなたの考え方を周りに伝えただけで,世界の1/3以上が変わるかもしれないほどの力があるとも言える.
ただ,この議論は,以下で議論するハブや,スケールフリー性を考慮していないので,十分でないことには注意しておいてほしい.
・scale-free(スケールフリー)
実際のネットワークを見てみると,1人の人や1つの組織,1つのウェブサイトがたくさんの人の連絡先や,多くの情報を持っているなんてことはよくあることだ.
そのようなノードを「ハブ(hub)」という.
ここで,議論するスケールフリー性は,本ノートの最初に少し議論した,Zipf's law(都市の人口と順位のスケーリング則)のネットワーク版と考えられる.
実際に現実のネットワークを調べてみると,Zipf's lawのように,
ネットワーク内で無作為に選んだ1つのノードが次数$${k}$$を持つ確率$${p_k}$$について,以下のスケーリング則が成り立つ:
$${p_k \sim k^{-\gamma}}$$
このスケーリングはハブの存在を意味している.
すなわち,人々のコミュニティなどで,たくさんの人につながる1個人,いわば,有名人が存在することを意味する.
注意:スケールフリー,scale-freeの意味
スケールフリーの意味は,ネットワークの次数分布$${p_k(k)}$$(1つのノードが次数$${k}$$を持つ確率)のグラフを描いたときに,特徴的なスケール(特徴的なピーク)が現れない(フリーである)ことを意味している.
*Barabasi-Albert model (バラバシ・アルバートモデル)
現実のネットワークは,スモールワールド性を基本に抑えつつも,スケールフリー性(ノードには大量のリンクを持つハブが存在する状況)が観察されている.では,これらの性質をうまく表現したネットワークの有名なモデルとして,Barabasi-Albert model(バラバシ・アルバートモデル)が知られている.
・設定:Barabasi-Albert model
このモデルでは,ノード総数$${n_0}$$を持つネットワークに対して,ノードを1つずつ追加していくことを考える(成長するネットワークを考える).
ただし,ノードをネットワークに追加するときに以下の条件をつける:
-成長(ネットワークは徐々にランダムにつながって大きくなっていく)
各ステップごとに新たなノードを1つ加えるが,
その際にすでにある$${n(t) = (t-1) + n_0}$$個のノードのいずれかにリンクを必ず接続していく($${t}$$はステップ数).
-優先的選択(たくさんのノードに繋がりやすいハブの存在を仮定する)
1つのノードがネットワークに追加されるときに,ネットワーク内の各ノードの次数$${k_i}$$を用いて,$${i}$$番目のノードに新たなノードがリンクされる確率$${\Pi(i)}$$は,
$${\Pi(i) = \frac{k_i}{\sum_i k_i}}$$
で与えられる.
この条件によって,成長と優先的選択という,新たなノードはより多くのリンクを持つノードに繋がりやすいシステムが導入される.(これは先のBonabeauモデルで議論してきたような,より強いものがより強くなるといった格差を生む構造にも相当していると言える.)現在の優先選択は$${k_i}$$に対して線形だが,これに非線形性を持たせるモデルや,コネクションへの適応度(分断のモデルのように性格的に繋がりやすいノードを仮定)を考慮することなど多くの改良が行われている.
(この辺りも多くの発展があるので,機会があればまたノートなどにまとめたい.)
ちなみに,このモデルの次数分布は以下のように求められている:
$${ p_k = \frac{2n(n+1)}{k(k+1)(k+2)} \sim k^{-3} (k \gg n) }$$
この結果は,このネットワークがスケールフリー性を再現していることを示している.
多くの改良されたモデルは存在するが,ここでは一旦ここで,このモデルの議論は終えたいと思う.
まとめると,現実のネットワークでは,ネットワークが成長していくだけでなく,ハブという多数のリンクが繋がりやすいノードが存在するという,優先的選択が起こっているのかもしれないと言える.
私たちは,生まれつき不平等であることを薄々自覚しているはずだ.
親ガチャと揶揄されたりするように,新たにネットワークに追加される際に,接続されるのが,(人脈だけでなく,資本的)コミュニティのハブであれば,有利だったりすることもある.
これは,「富める者はますます豊かになるだろう」とも言われる,マタイの福音書から由来して,”マタイ効果”と呼ばれているそうだ.
つまり,このモデルはある意味で残酷だろうが,
不平等性はあらかじめ備わったアルゴリズムなのかもしれない,
ということを示唆しているように見える.
人口減少への諦め:物理的制約としての受け入れ
ここまでの議論で大体わかってきたのは,地球規模での人口密度過多(人口密度が転移点を超えてしまった状況,$${\rho > \rho_c}$$)が起こってしまっているのではないかと考えられることだ.
これに付随して,社会の競争激化や戦争,エネルギー,水,食料不足,さらに,環境汚染の問題も起こっているように見える.地球温暖化に関しても同様の要因に起因している(特に,温室効果ガスの大量排出によるもの)とも科学的には考えられるが,より広く見れば,地球や太陽サイクル,その他の宇宙線などの要因かもしれない.
本題と少しずれるが,重要なこととして,以下を注意しておきたい:
科学は,仮定や予想に基づいて,モデル化,観測したもの,論理的に積み重ねた知識からの判断でしかなく,その枠を超えた未知な部分はわからない.つまり,「科学的だから」といっても,それが絶対的にあらゆる状況で正しいとは限らないし,わからないものはわからない(ただし,それが科学なら,すべての条件を同じく揃えれば.同じ結果が再現されるように,記述されているはず).その仮定や前提が正しくないかもしれないし,結果の抽出やその議論などに意図的な扱いがあるかもしれない.また,課題設定から結論まで,全体を通して,偏見や思いこみがあるかもしれない.(もちろん,このノートも例外ではない.)
現在直面している日本をはじめとして,その他の国で起こっている人口減少は,増えすぎた人口が要因であると考えられ,
先のモデルによれば,この人口減少はもはや,我々が当たり前に感じる重力といった,ものを掴んで離せば下に落ちるのと同じように,起こるべくして起こっている,物理的な制約とも言えてしまう.
つまり,より極端に言えば,人口密度過多な状況下での,少子化対策はもはや無駄と言えてしまう.
具体的には,出生数を増やそうとしても,物理的に無理な上に,もし増えたとしたら,より上記に挙げてきた社会問題は,特に首都圏,大都市圏ではさらに悪化するのである.
では,人口減少はもはや受け入れることが必要だ.
それを受け入れた上で,どんな問題が起こるだろうか?
本質的な社会問題:人口減少への諦めという視点から
主に以下のようなものがあるのではないかと感じる:
・孤立や孤独,家族がいない個人が増える
(社会規律,法律,倫理観などが未だこの移行に追いついていない?)
・社会インフラ維持がこれまで通りできるかどうか?
・医療技術などがあっても,それを施せる人が不足していく?
・困った時に助けてくれる人,会社,団体などがない不安
・食糧生産が十分に行えなくなる
この辺りが大きく問題になるのではないか?
(もちろんまだまだあるだろう…)
(それとも,これらは単なる不安で実際は問題ではないのかもしれない…)
解決案
上記のように,現在,直面している社会問題のほとんどは人口の急激な増加による「人口密度過多」を起源に持つものと,ここでは考えている.
そして,現在直面している,日本の人口減少は「人口密度過多」によるものである.この観点で社会問題に対する解決策を大まかに考えてみたい.
この解決策は多岐にわたって考えられるが,本ノートでは,社会物理学からのアプローチを考えていたので,ミクロ(個人レベル)とマクロ(社会レベル)の解決方法を考えてみたいと思う.
ミクロ:個人の思考のアップデート
そもそも人間は生物として,どう生きるべきだろうか?
いくつかのアイデアを列挙してみる.
*過去を忘却する
ボナボーモデル(Bonabeau モデル)からの知見を利用すれば,格差を是正したいのなら,人口密度はもちろんだが,戦闘の勝敗に関して,ノイズを高めたり,戦闘で得られる経験をできるだけ無視することが格差是正に影響していた.
それをヒントに考えてみると,
全ての人が過去の評価を気にせず,自信を持って生きることや,
ある人を評価するときに過去のことをあまり考えずに評価し認めること.
などが個人レベルでの思考や,意識改革として,格差是正には重要なのかもしれない.
*共依存関係の理解
人間以外の生物も支え合って生きている.
一見すれば,弱肉強食に見えるが,これは生物学における古典論のようなもので,捉え直す必要があるだろう.被食者はたくさん産んでいて個体数が多いし,捕食者は個体数が少ないことがほとんどだ.
つまり,捉え直すと,
被食者側は,食べられる分も考慮して,捕食者のためにたくさん産んでいるとも捉えられるし,
捕食者側は,被食者数を維持するために,その個体数を減らしているとも捉えられる.
このように生態系はバランスしあって,共生,共存をしている.互いに依存しあって,その強みと弱みの凸凹をうまくパズルのように食住関係を作って生きているのだ.
人間も同じように生きているはずなのである.そのツールとして,お金やテクノロジーの発展がある.人間は決して,お金を稼ぐために生まれたわけでもなければ,テクノロジーや経済の発展のために生まれたわけではないだろう.それらはあくまで,凸凹をうまく埋め合うのに使うツールとして,捉えておく必要がある.
さらに極端に言えば,お金もテクノロジーもその仕組みを誰も理解していなければ,役には立たない.その中では人は凸凹を埋め合うためのコミュニケーションをとって,互いに助け合っていく必要がある.助け合う,支え合う関係が人間の本質なのだろうと思う.
自分だけが良い思いをしたい,誰かよりも優れていたい,そんな気持ちは誰もが多少なりとも抱えているだろう.しかし,それも周りのおかげでそのような気持ちを抱けるのだ.あなたや,私が生きているのは周りのすべての存在のおかげである.(それは人間という種に限らない.ペットはもちろん,空気や無機質な物質も含めてすべての存在である.)
つまり,私がここで示したかった解決策の1つは,
万物に感謝し,相互作用しあって,依存しあって生きていることを自覚するという思想のアップデートが必要なのではないかという提案である.
争いなどしている場合ではない.万物に依存していることを自覚し,感謝しよう.
この取り組みは,先のモデルで言えば,
・対立や戦闘数の減少,場合によっては相互作用の大きさを弱める
・揺らぎの増加
による解決策である.
*性悪説から性善説に立ち返る
人は放っておくと,怠惰になるのか?
働いていない人間は怠惰だからなのか?
そんな前提を改めることを推奨している.
これは人口過多になって,競争社会にある今,人を信頼し合うのは難しい面があるかもしれない.
しかし,ボノボなど,猿などをみると,人類が進化してきたのは,助け合うことができたからだとわかるのだ.
また,性善説に関しては,以下の文献もヒントになるのかもしれない.
自らを犠牲にしてまでなぜ,他人に尽くすのか?という話のようだ.
(私はまだ,この本を読めていないので,いつか読みたいと思っている.)
*競争構造にあることを理解し,思い込みから脱却,自由な行動をとる
また,競争構造による官僚化,さらにビジネスの既得権益化が専ら進んでいることを理解しておくことが重要なのかもしれない.
すでにある学校や,その資格試験は本当に価値があるものだろうか?
皆が個人でその価値や意味を問い直し,改め,すでに用意されたレールに乗る意義を考え直す必要があるのかもしれない.
レオナルド・ダ・ヴィンチは観察眼と絵の描画を通して,芸術や,数学,物理,工学など幅広い分野に貢献していた.現代の枠組みにとらわれない成果の出し方である.既存の枠組みは何のためにあるか問い直し,自らのできる範囲でできる限りのことをすればいい.そこでは,各個人を同じ土俵で見ることなく,互いに尊重しあうことが大切かもしれない.
皆が同じようなレールに乗る必要は本当にあるのか?
凸凹を埋め合って互いに必要なサポートをし合う仕組みは作れないのか?
全ての組織の柔軟性が将来はますます試されていくに違いない.
*国,組織の存在を自覚,俯瞰し,忘却し,個人での繋がりを意識する
我々は生まれた時点で,国に所属している.それは官僚組織だ.
同様の文化的教育,言語教育がなされることで,各個人はみな類似の思想を”常識”として持つようになる.これにより秩序や安寧が保たれるわけだが,同時にグローバルな社会においては,異なる思想を持つもの同士,すなわち国や組織同士の戦争が起こりやすくなることを示す(分断モデルを参照のこと).
このシステムがあることを自覚し,国,外国人,日本人,組織人という単位で考えず,個人との繋がりを重視した生き方を理解する.相手は間違っていると決めつけたり,敵という関係を作らずに,ライバル,共存し合う仲間として理解する.地球を保護し,自らの生命はもちろん,周囲の生命を持続して,幸せに生きるための方法を探るという意識を持つ.
マクロ:社会とテクノロジーの発展
偶然か必然か,いや,私の視野が狭いせいかもしれない,
多くの解決の取り組みをちょっと考えてみると,
イーロンマスクが関わっているプロジェクトが多い気がしている.
(これも私の偏りが入っているだろう.これ以外の他の例もあるはずだ.)
*人口密度の制御:人類の居住面積を増やす
宇宙進出(例えば,火星移住)や,海底進出などで,居住面積を増やすことで,人口密度を適切にコントロールする.
仮想空間にも居場所をつくり,メタバースなどを発達させる.
*人口密度の制御:人口の時間操作
人口密度は $${\rho(t) = N(t) / S(t)}$$のように各時刻$${t}$$における人口$${N(t)}$$に依存している.この人口を制御する方法だ(ジェノサイドの方針は反対だ).そこで,ここでは時間操作を行う.例えば,非現実的だが,ある程度の人口をタイムトラベルで未来へ送ること(相対論や,冷凍保存を利用するなど).
*社会テクノロジーから個人レベルへの寄与:脳テクノロジーによる解決
ニューラリンク,Neuralinkでは,すでに何人かの両手両足麻痺の治験者に対して,脳に微小チップを埋め込み,コンピュータの操作などをできるように能力拡張させることに成功している.
このように,我々はすでに脳機能を理解し,そこから情報を取り出すことが可能になっている.
もちろん逆に,情報から脳機能へのアクセスもできるようになってきているだろう.(いずれもかなり怖い話ではあるが…)
これが進めば,脳波から,感情を読み取って,その人にあった生き方をできるように周りが配慮するなどしやすくなるだろう.例えば,個人レベルの倫理学や法律の策定も可能になるだろう.(現在の法律もデータにすれば個人の持つハードディスクなどに保存できるだろう,また,法律の取り出しにLLMが使える.)
*オンラインサロン
私は個人的にはオンラインサロンにいいイメージはない.理由はハブのような有名人が自身の新たな収益源にするために子供から大人まで信者を増やすようなやり方に見えてしまうからだ.ファンクラブのようなものとしても機能している側面が大きい.また,サロンを仲介する業者がもっとも稼げる仕組みに見える.
これらは私の情報不足や,偏見かもしれないが,このように個人の知名度に由来するやり方ではなく,より公共的な手法で参加できるオンラインサロンや,公園での公開青空教室といった方針で進むことはできないのかとも思っている.(現在,実際にその多くは新興宗教,ネズミ講,詐欺集会であったりすることも多く安全性が保証されていないのが難点だ.)
*仮想的な敵の構築,他生物種からの指示を受ける
社会的に協調し合うために,人類が皆仲間であるという環境を作る必要がある.そこで,宇宙からの侵略や,大規模自然災害が間違いなく来るという,仮想的な敵を用意する.その危機感をより強く煽って,人類全体で協力しなければという雰囲気を作る.もしくは,絶対的な神として,他生物種や,AIなどを信仰する.
(私は以上のアイデアは単なる思いつきで書いたものだ,あくまでもブレインストーミングで出てきたものの1つだ.)
*お祭り
私は祭事が1つの回答かもしれないと思っている.人類が仲間であることを神などを信仰することで,人類の協調性や創造性,あらゆる面を実装できていると思う.また,ひらかれた公共的な,非営利的な実行形態を持っていて,参加条件もないことがほとんどだ.特定の個人に対する信仰的側面も持たない.何かお祭り的要素によって,現在の分化して専門化してしまった要素を統合し,社会問題の解決,特に本質的な社会問題の解決に繋げられる可能性があるかもしれない.
*note.comのようなメディアサービス
このnote.comなどは年齢や立場,職種,思想なども問わずに誰もがこのような情報発信をサポートしている.私たちはこのような場を持てることに感謝しつつ,最大限それを利用し,楽しむことができるし,同時に社会問題に挑むことができる.
補足:エコロジカル・フットプリント
このノートでは具体的には取り上げなかったが,人口増加による環境資源の共有についての限度も考慮しておく必要がある.
エコロジカル・フットプリントは,そもそも地球という環境にどの程度の人口が収容できるのかを概算している.
データサイエンスが進み,あらゆる消費がデータ化でき始めた現代だからこそ,我々は最適な人口(人口密度)を探る時が来ているのだと思う.
まとめ
ここでは,私なりに,現在感じている大きな社会問題を取り上げ,社会物理学を学んでいく中で,感じた社会問題の起源と,その解決方法について大雑把に考察した.あくまでも個人の1つの試行実験のようなものだし,これはプロトタイプ(試作的なアイデア)である.問うて,学んで,考えていくプロセスの中で,また新たなアイデアが出てくるだろう.その都度,またこのようなノートを書こうと思う.
社会物理学的な観点を主体に今回は現代社会を考察してみたが,その勘所を掴めているかどうかは,より多彩な視点から考える必要があるだろう.例えば,人類全体や,個々人の現在に至るまでの考え方を探るには,人文社会学的観点や,歴史学,宗教学などを組み合わせる必要があるかもしれない(もちろん実践的にいろんな人と出会って個々人の考え方を探るのも重要だろう).さらには,将来的な問題解決には,これまでの過去も前提に,エンジニアリングはもちろん,心理学,脳科学,…と多岐にわたる分化してしまっている分野をきちんと全て統合させて整理し,年齢や職業,文化を超えた人々と共に考える必要がある.本来はそのような場がもっと活発にあればいいのだろうと思う.だからこそ,最初に述べた問題意識である,学校や大学といった場の改善が必要だと感じている.私自身が,この問題に何ができるかまだ模索中であるが,何かできることはないかを常に探っていこうとは思っている.
今回の学びを通して,この社会の問題点のおおよそ半分は私は解決できないのではないかと諦めている.人間が種を次世代へ繋ぐ遺伝子システムである以上,食物,資源争い,生殖活動など争いの元は必ずといっていいほど存在し続けるだろう.そして,地球上の人口密度が高くなったことで分断や,支配的官僚制,既得権益に縋る状況は必然と考えられる.
官僚制は共通の目的を持った個体が集まった場合に,大きな仕事を役割分担し,うまくこなすために機能してきた.現代はオートメーション化が進み,そのような役割分担を担う仕事は人類の一部だけが担えば良い状況になりつつあり,それは既得権益として,半国営的な企業などになりつつある.
少子高齢化の中で,この既得権益に縋っていられる若手はごく一部だけだろう.ほとんどの若手にとって,その既得権益を争って奪い合う時代はほぼ終わっている.特に若い人は創造性や,協調性,探求性の時代に生きている.だが,現代のシステムはいまだに官僚制ベースのシステムで回っている.一人一人に合った生き方ができるシステムは今後その需要をますます急速に増すだろう(例えば,シェアリングサービスや,LLMによる支援,スキマ時間でのサービスなどはその一例だ.これをさらに包括するような官僚制を覆せるシステムが今後大きな需要を持つのは間違いない).
人間は他の生物と異なり,時や場所を超えたコミュニケーション,理性的かつ,論理的,俯瞰的な思考ができる生物だろう.今回の知見を少しでも頭の片隅に意識した上で生活するだけでも,豊かな暮らしにつながるのではないかと期待している.
このような考察を通して,私なりに興味がある部分を日々探求し,一個人として学ぶことを楽しみつつ,今後も社会,世界,宇宙に関わっていきたいと思う.
[主な参考資料]
Castellano, Claudio, Santo Fortunato, and Vittorio Loreto. "Statistical physics of social dynamics." Reviews of modern physics 81.2 (2009): 591-646.
社会物理学: モデルでひもとく社会の構造とダイナミクス, 2022/10/25, 小田垣 孝 (著), 佐野 幸恵 (著), 山崎 義弘 (著), 山本 健 (著)
Saichev, Alexander I., Yannick Malevergne, and Didier Sornette. Theory of Zipf's law and beyond. Vol. 632. Springer Science & Business Media, 2009.
原文:Pósfai, Márton, and Albert-László Barabási. Network science. Cambridge, UK:: Cambridge University Press, 2016.
この記事が気に入ったらサポートをしてみませんか?
