ターンテーブル上を転がる球の不思議な運動
はじめに
「楽しめる物理問題200選」という、物理の問題集がある。

大学の学部生向けの問題集で、題材は主に古典物理学の範囲だが、なかなか興味深い問題が集められているのだ。一見難解に見えても、ある気付きを得ると簡単に解けるような「補助線一発解法」的な問題も多く、単なる演習書を超えた面白さがある。
この本で目を引いたのが、以下のような問題である。*印2つの難問指定。以下引用。
P99** オーストラリアのキャンベラにある科学博物館に、次のような装置がある。水平なテーブルの中央部から円板を切り取り、それを回転軸の上に乗せて、元の位置にはめ込んである。

上図に示すように、円板を回転させ、固いゴムボールをテーブル上で転がす。ボールが回転している円板に達すると、ボールは直線の道をはずれ、曲線の道に沿って進む。円板から出ると、ボールは元の直線の延長上の道を、滑らずに転がる。このときの速さは、円板に達する前の速さと同じである。この運動を説明するには、何の保存則を使えばよいか。
要は、テーブルの一部が(一定の角速度で回転する)ターンテーブルとなっており、その上を通るようにボールを転がすと、ターンテーブルのどこから進入しても、最後は必ず最初の直線軌道の延長に復帰する、と言っている。この問題を初見で「○○が保存するから」と即答できた人がいたらすごい。物理学で博士号を取った自分だが、この本を買った10数年前、真剣に考えても何の保存則が効いているのか思い付かなかった(上記のような運動になること自体は導けたが、保存量が分からなかった)。
以下で、まずは、何が保存されるかは置いておいて、ボールの運動が上記のようになる理由から考えよう。
自分なりの解法
この問題を最初に見たときに、とりあえずボールの運動を極力簡単に説明しようとして思い付いたのが、以下のような解法である。いきなり回転盤の上を転がる球の運動を考えるのは難しいので、単純な問題からステップを踏んで考える。
球の質量を$${M}$$, 半径を$${R}$$, 慣性モーメントを$${I}$$とする。大学の学部レベルの力学で習う通り、慣性モーメントは、
中身が詰まった密度が一様な球の場合: $${I = (2/5)MR^2}$$
中空の球殻の場合: $${I = (2/3)MR^2}$$
である。
STEP1: 動く床に球をそっと置く場合
さてここで、「動く歩道」のように、1方向に一定速度$${V}$$で動く床があり、そこにこの球をそっと置く状況を考える(下図)。球が床に接地した後、球の転がる速さはどうなるか?

床は速度Vで右方向に動いている。球を床に置いた瞬間、球には左回転のトルクが掛かるので、接地後、球は床に対して左回転することに注意(静止系に対しては速度vで右方向に動く)。
球を置いても床の速度は変わらず、また、球と床の間の静止摩擦力は十分大きく、球は床の上を常に滑ることなく転がるものとする。床に接地した後の球の速度を$${v}$$, 角速度を$${\omega}$$とする。接地する瞬間に球が床から受ける力を$${F}$$とすると、球の重心の運動と、重心の周りの回転に関する運動方程式はそれぞれ以下のようになる:
$${\displaystyle M{\frac{dv}{dt}} = F; \,\, I{\frac{d\omega}{dt}} = RF}$$ 式1
接地時のごく短い時間を$${\Delta t}$$とすると、上式から、
$${\displaystyle M\Delta v = F\Delta t; \,\, I\Delta \omega = RF\Delta t}$$ 式2
となり、$${F\Delta t}$$を消去して、
$${\displaystyle M\Delta v = \frac{I}{R}\Delta\omega}$$ 式3
となる。今の場合、最初は球は静止しているので、$${\Delta v = v}$$, $${\Delta \omega = \omega}$$である。また、設置後、床と滑らないために、
$${\displaystyle V-v = R\omega}$$ 式4
が成立しないといけない。これらを用いて式3を解いて、
$${\displaystyle v = \frac{I}{I+MR^2}V \equiv \gamma V}$$ 式5
を得る。ここで、
$${\displaystyle \gamma \equiv \frac{I}{I+MR^2}}$$ 式6
と置いた。$${\gamma}$$は球に固有の係数で、$${0 < \gamma < 1}$$である。特に、一様な球では$${\gamma = 2/7}$$, 球殻では$${\gamma = 2/5}$$である。
このように、動く床に球をそっと置いた場合、接地後の球の速度は、床の速度の$${\gamma}$$倍になる。この係数$${\gamma}$$が床の速度に依存しないのがポイントである。
STEP2: 球に初速度がある場合
では次に、球に初速度がある場合を考えよう。球は初めに静止した床の上を初速度$${v_0}$$で転がり、途中から速度$${V_1}$$で動く床に乗る状況を考える。動く床に乗った後の球の速度$${v_1}$$はどうなるか?

球は初めから右向きに転がっているので、角速度の符号は右回りを正にとる。
考え方はSTEP1と同じで、運動方程式は以下になる(回転運動の方の式の符号に注意):
$${\displaystyle M{\frac{dv}{dt}} = F; \,\, I{\frac{d\omega}{dt}} = -RF}$$ 式7
これより、$${F\Delta t}$$を消去して、
$${\displaystyle M\Delta v = -\frac{I}{R}\Delta\omega}$$ 式8
を得る。ここで、$${\Delta v = v_1-v_0}$$であり、また、滑らない条件は、
$${R\Delta\omega = (v_1-V_1)-v_0}$$ 式9
となる。これらを用いて式8を解くと、
$${\displaystyle v_1 = v_0 + \gamma V_1}$$ 式10
が得られる。STEP1の場合と比べると、終状態の速度は$${\gamma V_1}$$に初速度を加えただけであることが分かる。
STEP3: 速度の異なる2つの床を順に転がる場合
さらに今度は、速度の異なる2つの床を順に転がっていく場合を考えよう。下図のように、球が初速度$${v_0}$$で2つの床(それぞれ速度$${V_1}$$, $${V_2}$$で動く)を順に転がっていくときの、それぞれの床の上における速度を$${v_1}$$, $${v_2}$$とする。$${v_2}$$はどうなるか?

これまでとまったく同様に考えると、運動方程式は、
$${\displaystyle M(v_2-v_1)=-\frac{I}{R^2}\left\{(v_2-V_2)-(v_1-V_1) \right\}}$$ 式11
となり、式10を代入して解くと、
$${v_2 = v_0 + \gamma V_2}$$ 式12
となる。何と、床1の速度$${V_1}$$には依存しないのだ。球の速度は、その時点で球が乗っている床の速度と、初速度のみで決まることになる。意外な結果ではないだろうか?ある時点における球の速度は、それまでにどのような経路でどのような速度を動く床を通ってきたかという履歴には全く依存しないのである。
STEP4: 一般化
ここで一気に飛躍するが、上記の「履歴に依存しない」という結果を2次元に拡張すると、直ちに次の性質が成り立つことが分かる。
2次元平面の床があり、その床は、場所によって異なる方向に動いているとする。具体的にどのようなモノか想像しにくいが、小さな「動く歩道」が敷き詰められていて、その動く方向や速度が場所によって異なる(ただし、同じ場所では一定の速度で動く)ような状況を想像する。床の速度は、位置$${(x, y)}$$で決まるので、速度場$${\vec V(x, y)}$$で表すことができる。このとき、球を初速度$${\vec v_0}$$でこの床の上を転がした場合、球の位置$${(x, y)}$$における球の速度は
$${\vec v(x, y) = \vec v_0+\gamma \vec V(x, y)}$$ 式13
となる。
簡単な例として、下図のように、床の領域1, 2がそれぞれ速度$${\vec V_1}$$, $${\vec V_2}$$で動いているとしよう。

領域1と領域2が異なる速度で動いている。
ここに、球を初速度$${\vec v_0}$$で転がすと、領域1, 2における球の速度は、それぞれ、
$${\vec v_1 = \vec v_0 + \gamma \vec V_1}$$,
$${\vec v_2 = \vec v_0 + \gamma \vec V_2}$$
となる。球の転がる軌道を求めるには、上図に示したように、$${\vec v_0}$$, $${\vec v_1}$$, $${\vec v_2}$$のベクトルを延長してつなげればよい。最後に$${\vec V=0}$$の動いていない床に球が降りると、球の速度は初速度に復帰する!ただし、元に戻るのはあくまでベクトルとしての速度であって、上図に示したように、最後の軌道が最初の軌道の延長に復帰するとは限らない。
STEP5: ターンテーブルの場合
最後に、上記の解法をターンテーブルの場合に応用しよう。回転盤の速度ベクトルを図示すると下図のようになる。$${\vec V}$$の大きさは中心からの距離に比例して大きくなる。

この$${\vec V}$$を一律$${\gamma}$$倍して、さらに、球の初速度$${\vec v_0}$$を一律に加えると、下図のようになる。

回転盤左から球が転がってくる状況を想定。回転盤の速度場のγ倍(黒)に初速度ベクトル(青)を加算したものが、球の転がる速度(赤)となる。
転がる球の軌道を求めるには、この合成ベクトルを接線とするように線を引けばよい(下図)。

このように、球がどの位置から回転盤に入射しても、盤を降りたあとは、最初の軌道の延長の直線に復帰する!
※上図の回転盤上における球の軌道は、球の重心座標の運動方程式を立ててきちんと解くと、ある半径の円弧になることが示される。証明は力学の演習書(後藤憲一「力学演習」等)に載っており、数学セミナー誌の記事にも平易な証明がある(時枝正, 2014. 回転盤をよぎるボウリング.数学セミナー, 53(4): 2-5)。
で、、保存量は?
では、最初の問に立ち戻って、この運動を「保存量」で説明するにはどうしたらよいでしょう?上記の解法も、元をたどれば運動方程式を解いているだけで、何かの保存則をテクニカルに使っているわけではない。残念ながら自分では思いつけず、本書の解答を見ると、記述は以下の通り。

意味、分かるだろうか? 角運動量というと、直観的に球の中心を基準に考えたくなるのだが、そうではなくて、基準点を球が転がる床面上に設定するのがポイントなのである。
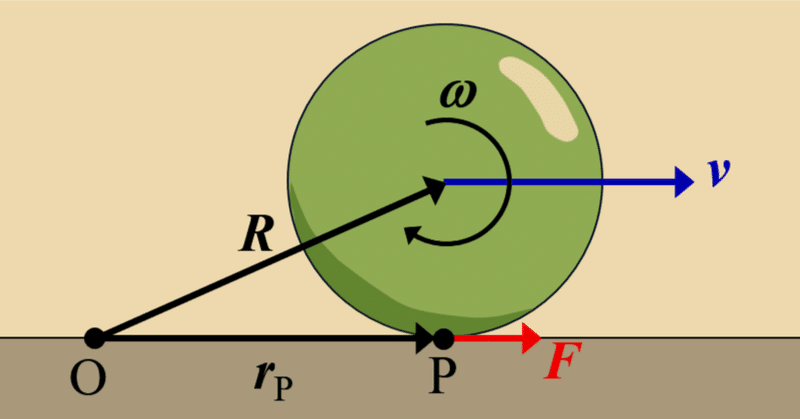
下図のように、位置ベクトルの基準点$${\text O}$$を床面上にとり、床が動くときに球に作用する力$${\vec F}$$のトルク$${\vec N = \vec r_{\text P}\times\vec F}$$を考える。$${\vec r_{\text P}}$$と$${\vec F}$$が常に平行なため、常にトルクはゼロ$${\vec N = 0}$$である。

したがって、球が転がる間、床がどのように動いて球にどのように力が作用しようが、床面上の点を基準とした球の角運動量$${\vec L = \vec R \times M\vec v + I\vec \omega}$$の水平成分は常に保存されるのだ。
回転盤の問題の場合、床面上に$${xy}$$座標を設定し、$${x}$$方向を球の初速度の方向にとり、$${y}$$方向をその垂直な方向にとると、$${y}$$方向の角運動量$${L_y}$$の初期値はゼロであるため、球が回転盤を通り過ぎた後も、$${L_y=0}$$でなければならない。したがって、回転盤を降りた後の転がる方向は必然的に$${x}$$方向となる。しかし、これだけでは、回転盤を降りた後の軌道が最初の軌道の延長に復帰するとは限らない(図4の場合ように、軌道が横方向にずれることもあり得る)。上記本書の解答の文面ではこの辺が説明不足である。一定の角速度で回転する回転盤の場合、球が$${y}$$方向に受ける力は、$${+y}$$方向と$${-y}$$方向でちょうど対称になるため、元の軌道の延長に戻るのである。
簡単な実験
上記の性質の帰結は、球が最初に静止している場合、床をどのように動かしても、床が止まったら球も止まる、ということである。回転盤を用意しなくても、この性質だけなら検証できそうである。ゴム製のスーパーボールを用いて、ちょっと実験してみたのが、下の動画。
下手な動画だが、下の動かしている紙を止めると、球もだいたい止まるのが分かると思う。一見当たり前のようだが、これを説明しようとすると上記の説明になるわけで、決して自明ではない。
おわりに
以上、なかなか教育的な問題でした。古典力学の問題は、実際に模型を作って運動を再現しようとすると、摩擦や空気抵抗などが絡んで簡単にはできないものが多いが、この「球が転がる」系の問題の場合、球と床面との間の摩擦力は大きければ大きいほど良いので、再現しやすいのである。冒頭に書いたように、本書の設問によると、オーストラリアのキャンベラにある科学博物館に展示がある(あった?)ようだが、国内各地にある子供向けの科学館などでも模型で実演して見せたら、角運動量の保存則を実感する例として、面白いかもしれない。
この記事が気に入ったらサポートをしてみませんか?
