
ベルヌーイ試行
コイン投げのように、二つの異なる結果をもイベントを、前のイベントの結果とは独立に、延々と実行する確率的イベントの連鎖はベルヌーイ試行とよばれます。
いま二つの結果をa, bとし、それぞれがp, qの確率で起こるとします。ここで規格化条件p+q=1が成立していると仮定します。(コイン投げの例では、コインの縁で立つ、などの結果はないとみなすことに対応します。)

非常にシンプルな設定にも関わらず、このモデルが適用できるプロセスは数多くあります。ここでモデルとは、(たいてい)ある特殊なプロセスに着目し、それを数学的に記述したものです。
プロセスは、抽象的に言い換えると時間発展する物理量であり、たとえば人口の増加や、渋滞の形成、燃焼領域の拡大、心臓の鼓動、流体の渦生成、連続コイン投げ、生物ネットワークの形成と崩壊、惑星の運動、昆虫の形態変化、情報の伝搬、素粒子崩壊など、時間・空間スケールについても、注目する物理量についても、非常に多岐にわたります。
それらのプロセスをある特定の意味で再現するような、数学的記述があると仮定します。(ニュートンの運動方程式などその例です。)
その記述が複雑であるほど、実際のプロセスをうまく再現する傾向にあり、また記述がシンプルなほど、実際のプロセスとの定量的な一致まではいかずとも、それを定性的に再現でき、さらに元のプロセスとはまったく別のプロセスに対しても適用できることが多くなります。

つまり、プロセスのモデル化とは、そのプロセスを数学的に抽象することにほかならないわけですが、それが本質的なものであるほど、そのプロセスのみでなく、他のいく通りもの異なるプロセスのモデルとしても使えることが多いのです。不思議です。ウィグナーは"The Unreasonable Effectiveness of Mathematics in the Natural Sciences"のなかで、モデルとプロセスの関係を鍵とドアにたとえて以下のように表現しています[1]:
We are in a position similar to that of a man who was provided with a bunch of keys and who, having to open several doors in succession, always hit on the right key on the first or second trial. He became skeptical concerning the uniqueness of the coordination between keys and doors.
ベルヌーイ試行の例では、元のプロセスが連続コイン投げであったわけですが、このモデルはくじ引き(あたり、はじれ)や、微粒子のランダムな運動(ある方向進むか進まないか)などにもあてはめることができます。
さらに、母集団からの無作為抽出のモデル化ともみることができます[2]。たとえばあるグループから無作為に幾人か選び、喫煙者かどうかを調べるのは、ベルヌーイ試行とみることができます。また品質管理において、不良品かそうでないかを異なる二つの結果とし、ベルヌーイ試行とみなすことも考えられます。ベルヌーイ試行は前後の結果が独立だと仮定するので、モデルを適用して実際のデータがそこから有意にずれている場合、機械になんらかの変化が生じたことを検出できます。
さて、独立したイベントの回数がNのベルヌーイ試行を考えてみます。コイン投げでしたらコインを投げる回数です。このNは非常に大きいと考えてください。
二つの結果はa, bなので、得られた結果を表にするとしたら以下のようになるでしょう:

たとえばaがn回出て、bがN-n回出たとすると、このような結果の列が出る確率は、a, bの出る順序に関係なく、

となります。一方、このような結果の列の総数は、N個の場所からn個を選び出すパターンの総数に等しく、
N! / [n! ・ (N - n)!]
となります。ここでスターリングの公式

を使うと、次のように変形できます:

ここでH(x)は実測エントロピーに他なりません。
Nは非常に大きいとすれば、指数関数の肩の部分は、非常に大きい数×滑らかに変動する関数の形をしています。またさらに、x=n/Nは、Nが十分に大きければ、連続変数とみなせるでしょう。このとき、上の式の値は、H(x)を最大にするxの値の付近で鋭いピークを持ちます。

ところでH(x)は実測されたエントロピーなので、x=1/2で最大値log2をとります。つまりnがN/2であるとき、そのような結果の列の総数は最大値をとるということです。x=1/2を代入すると、
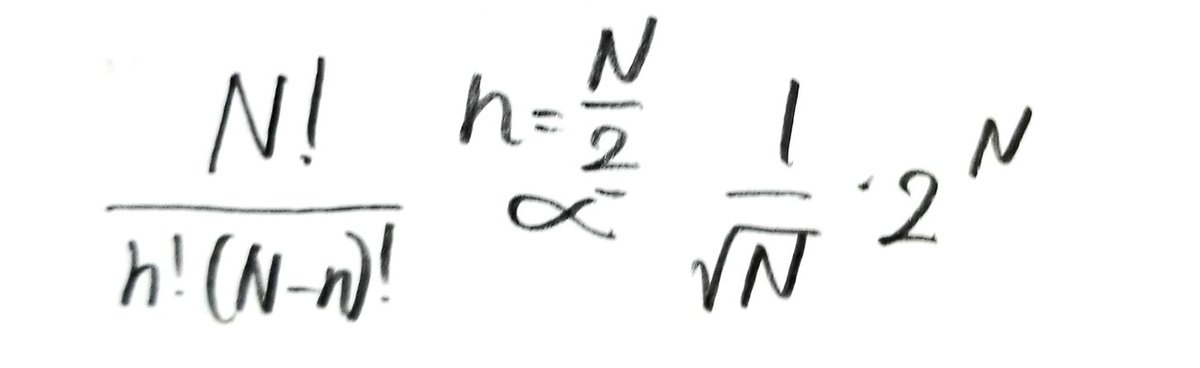
がわかります。長さNの結果の列のパターンの総数は2のN乗個ですから、上の結果は、Nが大きいとき、nがN/2に近い結果の列が、パターンの総数のほとんどすべてを占めているということです。これを実際に確かめることができます。エントロピーを最大値付近でテイラー展開すると、

となるので、これを代入し、最大値のごく近傍で積分すれば、

となるのがわかります。計算の途中、指数関数に比べて変動がゆるやかな係数部分は、指数関数を最大にするxの値を代入して積分の外に出しています。また、積分範囲を実数全体へと拡大していますが、Nが大きいとx=1/2から少し離れただけで被積分関数の値は無視できるくらい小さくなるので、妥当な近似なのです。
ここからは確率もこみで考えてみます。結果aの回数がnであるような列の個数に、それが実現する確率を掛ければ、N回のベルヌーイ試行において、aがn回出る確率が求められます。これをPnと書くと、再びスターリングの公式を用いて、

相対エントロピーは非負であり、x=pのときに限り最小値ゼロをとります。これまでの議論と同様に、Nは非常に大きいため、x=p付近で鋭いピークを持つことになります。そのような結果の列の個数とそれが実現する確率は、それぞれ

となります。つまりベルヌーイ試行を長く続けると、その結果の列は、ほとんど確実にaをpだけの割合で含むことになり、そのような列の数は列の長さNに指数関数的に依存していて、その増大の速さを定めているのがエントロピーなのです。
またさらに、xがpでないような「ありえない」結果の列は、その確率がNの増大とともに指数関数的に減っていき、その減少の速さを決めているのが相対エントロピーなのです。このように、典型的な結果ではない結果が、どのように減衰していくかを定める関数をrate functionといい、確率的イベントの特異性(典型から外れた結果の性質)を特徴づけます。
次回はより複雑な、二状態マルコフ連鎖に関しても同様な解釈ができることをみていきます。
参考文献
[1] E.P.Wigner, "The Unreasonable Effectiveness of Mathematics in the Natural Sciences," Communications on Pure and Applied Mathematics 13, 1 (1960).
[2] W.Feller, "An Introduction to Probability Theory and its Applications," 3rd ed. (Wiley, New York, 1968), Vol. 1.
[3] L.-S.Young, "Some Large Deviation Results for Dynamical Systems," Transactions of the American Mathematical Society 318, 525 (1990).
