Hayato式!! 応用情報技術者試験 ~~アルゴリズム・過去問編~~
前編でアルゴリズムについて学びましたが、今回はその知識を実際に使ってみましょう。
問1 (応用情報技術者試験 令和4年秋 午前 問6)

ア: クイックソート イ: 選択ソート
ウ: 挿入ソート エ: バブルソート
解説は目次から飛んでください!
問2 (応用情報技術者試験 令和3年秋 午前 問5)
バブルソートの説明として,適切なものはどれか。
ア: ある間隔おきに取り出した要素から成る部分列をそれぞれ整列し,更に間隔を詰めて同様の操作を行い,間隔が1になるまでこれを繰り返す。
ィ: 中間的な基準値を決めて,それよりも大きな値を集めた区分と,小さな値を集めた区分に要素を振り分ける。次に,それぞれの区分の中で同様の操作を繰り返す。
ウ: 隣り合う要素を比較して,大小の順が逆であれば,それらの要素を入れ替えるという操作を繰り返す。
エ: 未整列の部分を順序木にし,そこから最小値を取り出して整列済の部分に移す。この操作を繰り返して,未整列の部分を縮めていく。
問3 (応用情報技術者試験 平成26年秋 午前 問6)
データ列が整列の過程で図のように上から下に推移する整列方法はどれか。ここで,図中のデータ列中の縦の区切り線は,その左右でデータ列が分割されていることを示す。

ア: クイックソート イ: シェルソート
ウ: ヒープソート エ: マージソート
問4 (応用情報技術者試験 平成21年春 午前 問8)
相異なるn個のデータが昇順に整列された表がある。この表をm個のデータごとのブロックに分割し,各ブロックの最後尾のデータだけを線形探索することによって,目的のデータの存在するブロックを探し出す。次に,当該ブロック内を線形探索して目的のデータを探し出す。このときの平均比較回数を表す式はどれか。ここで,mは十分大きく,nはmの倍数とし,目的のデータは必ず表の中に存在するものとする。
ア: m+n/m イ: m/2+n/2m
ウ: n/m エ:n/2m
問5 (応用情報技術者試験 平成26年秋 午後 問3)
マージソートに関する次の記述を読んで,設問1~3に答えよ。
マージソートは,整列(ソート)したいデータ(要素)列を,細かく分割した後に,併合(マージ)を繰り返して全体を整列する方法である。
ここでは,それぞれの要素数が1になるまでデータ列の分割を繰り返し,分割されたデータ列を昇順に並ぶように併合していくアルゴリズムを考える。例として,要素数が8の場合のアルゴリズムの流れを図1に示す。

再帰呼出しを使って記述したマージソートのアルゴリズムを図2に示す。

図2のアルゴリズムを連結リストに対して実行するプログラムを考える。ここでは,整列対象のデータとして正の整数を考える。連結リストは,複数のセルによって構成される。セルは,正の整数値を示すメンバ value と,次のセルへのポインタを示すメンバ next によって構成される。連結リストの最後のセルの next の値は,NULLである。連結リストのデータ構造を図3に示す。

〔連結リストの分割〕
図2中の(2)の処理を行う関数 divide を考える。関数 divide は,連結リストの先頭へのポインタ変数 list を引数とし,分割後の後半の連結リストの先頭へのポインタを戻り値とする。連結リストの分割前後のイメージを図4に示す。

連結リストをセルの個数がほぼ同じになるように分割するために,ポインタ変数を二つ用意し,一方が一つ進むごとに,他方を二つずつ進める。後者のポインタが連結リストの終わりに達するまでこの処理を繰り返すと,前者のポインタは連結リストのほぼ中央のセルを指す。この方法を利用した関数 divide のプログラムを図5に示す。以下,連結リストのセルを指すポインタ変数を a とするとき,aが指すセルのメンバ value を a->value と表記する。

〔連結リストの併合〕
図2中の(4)の処理を行う関数 merge を考える。関数 merge は,二つの連結リストの先頭へのポインタ変数 a と b を引数とし,併合後の連結リストへの先頭へのポインタを戻り値とする。併合処理を行う際には,ダミーのセルを用意し(そのセルへのポインタを head とする),この後ろに併合後の連結リストを構成する。a と b が指すセルの値を比較しながら,値が小さい順に並ぶよう処理を進める。連結リストの併合の流れを図6(処理は,①,②,③,…と続く)に,関数 merge のプログラムを図7に示す。
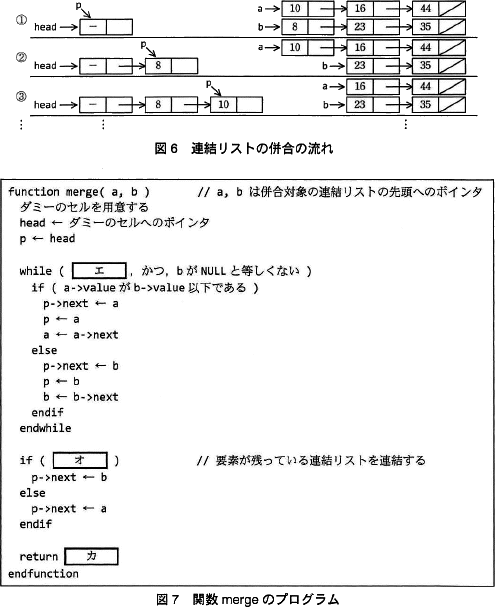
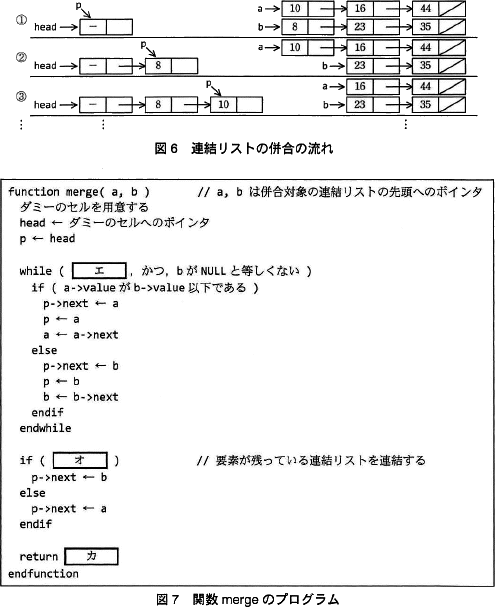
問5 設問1
〔連結リストの分割〕について,(1)~(3)に答えよ。
(1) 図5中のア~ウに入れる適切な字句を答えよ。
(2) 図3の連結リストに対して関数 divide を実行し,プログラムが図5中のαの部分に達したとき,ポインタ変数 a は,図3中のどのセルを指しているか。指しているセルの値(valueの数値)を答えよ。
(3) 奇数 2N+1 個のセルから成る連結リストを関数 divide で分割すると,前半と後半の連結リストのセルの個数はそれぞれ幾つになるか式で答えよ。
問5 設問2
図7中のエ~カに入れる適切な字句を答えよ。
問5 設問3
32個のセルから成る連結リストに対し,図2のアルゴリズムに相当するプログラムを実行した場合,関数 merge は何回呼び出されるか答えよ。
わかりやすい解説!!
問1 解説
~注目するポイント~
w ← A[j]
A[j] ← A[jー1]
A[jー1] ← w の箇所
~この箇所で言っていること~
A[j] の箇所にA[j-1] を代入していることから、調べたい要素の隣の要素と比較して、交換していることがわかる。
~復習~
この内容はアルゴリズム編その2にてやった内容です!
これを見ると、バブルソートが同じことを言っていますね!
よって答えは「エ」の一択しかありません。
問2 解説
アルゴリズム編その2よりバブルソートの内容を調べると、
「バブルソートとは、データ内で隣り合う要素の大小を比べながら並び替えることです」とある。
きちんと覚えていましたか?
この内容がわかっていたら、答えは一瞬で出たと思います!
「隣」・「大小」というワードに注目すれば答えは「ウ」しかないですね!
問3 解説
下の図を見ると、8つのブロックが何個かのグループに分けられて、合体していることがわかる。

~ここで復習~
アルゴリズム編その2にて「整列済みの2つの配列を合体して1つにして整列するという手法」という説明が書いたソートがある。
思い出せましたか?
正解は「マージソート」です。
ほかの選択肢は絶対にありえませんよね!
この問題を解くうえで重要なの「合体」ですね。これに気づけば簡単だったと思います。
問4 解説
問題中に「線形探索」とある。
アルゴリズム編その1にて解説している通り線形探索とは、「ある要素の先頭から1つずつ探索したいものに合致しているかどうかを調べていく方法」である。
ちなみに線形探索の平均比較回数は、先頭から一つずつ比較していくため、n個のデータの中から調べたいもののデータを探すとき、
(n+1)/2回・・・① かかる。
これを踏まえて問題文を上から1文ずつ分析してみましょう。
1. 「相異なるn個のデータが昇順に整列された表がある。この表をm個のデータごとのブロックに分割し,各ブロックの最後尾のデータだけを線形探索する」とある。
つまりn個のデータをmこのブロックに分けると書いてあり、各ブロックの最後尾のデータを調べるので調べるデータ数はn/m個となり、①に代入すると平均比較回数は (n/m+1)/2 回と表すことができる。
2. 「当該ブロック内を線形探索して目的のデータを探し出す」とあるが、これは「1.」にてみつけたブロックを線形探索するので、調べるデータ数は当然 m 個ですね!
よって①に代入すると平均比較回数は (m+1)/2 回と表すことができます。
となると、ここまで読んだ大半の方はおそらくこう思うはずです。
「1.と2.の平均比較回数を足せば終わりじゃない??」
実際に足してみると、
(n/m+1)/2 + (m+1)/2 回 ・・・② となるはずです。
じつは本来ならこれで正解なのですが、今回の場合は選択肢に上の回答がないことに気づきましたか?
ここで最も注意しなければならないのが問題文中の
「mは十分大きく,nはmの倍数とし,目的のデータは必ず表の中に存在するものとする」 です。
ここで②の式を変形してみましょう。
(n/m+1)/2 + (m+1)/2 = n/2m + m/2 + 1
となります。
なぜ式変形をしたかというと、理由は「+1」の存在です。
「mは十分大きい」と書かれていますが、n/mは大きいとは限らないのです。
n/mはmが大きくなればなるほど、nの値が変わらなければどんどん小さくなります。
例: 1/2=0.50
1/4=0.25 のように
すなわち「+1」という存在が邪魔なのです。
なので式変形をしました。
「n/2m + m/2 + 1」という式にも「+1」は入ってますね。
しかし、この式の「+1」は実は無視できてしまうんです!
いったいなぜでしょうか?
正解は「m/2」の存在です。
n/2mは先ほど説明した通り、mが大きくなればなるほど、nの値が変わらなければどんどん小さくなります。
しかし、「m/2」はどうでしょう?
mが大きくなればなるほど、どんどん大きくなることがわかりますね!
例: m=4の時 m/2=2
m=100の時 m/2=50
m=∞の時 m/2=∞/2 となる。
となると、「+1」は無視できますね!
よって正解は「m/2+n/2m」となりますね。
問5 解説
設問1
(1)アが含まれるコメントに、「連結リストの終わりまで繰り返す」とかかれていますね!
これがヒントです。
ここで一つ質問です。
そもそも「連結リストの終わり」とはいったいどのような状態のことを言うのでしょうか?
それは、次のリストのポインタが「null」になる時です。
要するに「null」になるとき、繰り返しが終了します。
プログラムを見ると「ア」に入る場所では、繰り返しが終了してはいけないので、「ア」に入る語句は「 b が null と等しくない」に近い言葉が書かれていれば正解となります!
「ィ」:図4の下の文章内に「ポインタ変数を二つ用意し,一方が一つ進むごとに,他方を二つずつ進める」とあります。これは、連結するリストをセルの個数がほとんど一緒になるように分けるために行う動作です。
また、「後者のポインタが連結リストの終わりに達するまでこの処理を繰り返すと,前者のポインタは連結リストのほぼ中央のセルを指す」とあるので、aを1つ、bを2つ動かす必要があり、「if」の前まででそれぞれ1ずつ動かしているのでbをもう1回動かす必要がある。
よって、b←b->next が正しいことがわかります。
「ウ」:図4より連結リストを分けるには、後半リストの連結を消す必要があります。また、ィの過程を用いると、aの次のセルポインタであるnext にNULLを代入して後半リストの連結を消します。よって、a->nextが適切となります。
(2)ィの過程にてaは1つ、bは2つ進むことがわかっている。
すなわち、bが終端の8番目に達したときaは4番目に達しています。よって図3より先頭から4番目なのは「8」となりますね!
(3)図5のプログラム中の
if (bがNULLと等しくない)
b ← b->next の箇所に注目してください。
b がNULLのときには2回目の進みが行われないことがわかる。
つまり、リストの大きさが5ならば{a=3、b=5}、リストの大きさが9ならば{a=5、b=9}というような状態でwhileループが終了します。a の位置から前の要素が前半リストとなるため、大きさ5の場合には前半が3つで後半は2つ、大きさ9の場合には前半が5つで後半は4つというように分割されます。これをNを使って一般化すると、前半の連結リストのセルの数はN+1個、後半の連結リストのセルの数はN個となりますね。
設問2
「エ」: 図7のプログラム7~15行目で、a->value と b->value を比較して、小さい方をpに追加する処理を行っている。
→a と b の両方の連結リストにセルが残っている必要がありますね!
残っていなかったら比較なんてできませんもんね!
よって、「エ」に入る処理は「aがNULLと等しくない」と似た意味になれば正解です。
「オ」: 図7のプログラム6行目の継続条件は「aがNULLと等しくない、かつ、bがNULLと等しくない」です。
となれば、18行目以降はリストの終端に達した際に行う処理となります。図6とプログラムを見ながら併合動作を確認すると、a がNULLのときには b を p の後ろに連結させ、b がNULLのときには a を p の後ろに連結させる処理が必要となることがわかりますね!
[オ]が真のときには、p->next ← b で、b を p の後ろに連結されていますが、これは a がNULLのときに行うべき処理でしたね。
よって、「aがNULLと等しい」または「bがNULLと等しくない」が最適だと思われます。
「カ」
関数 merge の戻り値が入ります。戻り値については、問題文の〔連結リストの併合〕に、「併合後の連結リストへの先頭へのポインタを戻り値とする。」とあるので、先頭へのポインタを示す式を考えます。
図6「連結リストの併合の流れ」でリストの先頭を指すポインタが head になっていること、及びプログラム中でダミーのセル head の後ろに p を連結していることから、ポインタ変数 head のメンバ next が指すセルが、併合後の連結リストの先頭であることがわかります。
よって、[カ]には「head->next」が入ります。
設問3
32個のセルから成る連結リストに対して、図2のアルゴリズムに相当するプログラムを実行した場合、(1)~(3)が実行されることで各1個のセルを持つ32つのリストに分割されます。
マージソートでは隣り合ったリスト同士を整列しながら併合していくことを繰り返します。併合は次のように進んでいきます。
1要素×32リストを2つの要素を持つ16つのリストにする。ここで関数 merge が16回呼び出される。
2要素×16リストを4つの要素を持つ8つのリストにする。ここで関数 merge が8回呼び出される。
4要素×8リストを8つの要素を持つ4つのリストにする。ここで関数 merge が4回呼び出される。
8要素×4リストを16つの要素を持つ2つのリストにする。ここで関数 merge が2回呼び出される。
16要素×2リストを32つの要素を持つ1つのリストにして、併合完了。ここで関数 merge が1回呼び出される。
よって、関数 merge が1回呼び出される回数は、
16+8+4+2+1=31回
となります。
(参考:https://www.ap-siken.com/kakomon/26_aki/pm03.html)
いかがでしたでしょうか。
どれくらい正解できましたか?
次回は「コンピュータの構成要素」という範囲に入っていきます!
この記事が気に入ったらサポートをしてみませんか?
