ファジィ集合のはなし(6)
含まれる含まれないの二者択一をやめてどっちつかずも許してしまう集合、ファジィ集合のはなし。今回はいよいよ「大体の数同士の足し算」に入ります。
いきなり足し算をする前に、ファジィ集合の元どうしの演算をどう組み立てるか考えます。
端的にやりたいことを言うと、普通の集合からファジィ集合を作る方法を見ます。
前回見たようにファジィ集合はファジィではない普通の集合(クリスプ集合)と繋げることができます。
例えば$${\alpha-}$$カットはメンバーシップ関数が$${\alpha}$$以上になる範囲(元)だけを集めた集合でした。
このように、ファジィ集合から普通の集合を作ることを見てきましたが、その逆、普通の集合からファジィ集合を作る手法はまだ触れていません。
この「ファジィ集合の構成」を決めるのが分解定理です。
ファジィ集合を構成するというのは、各元ごとにメンバーシップ関数の値を与えること、もっと平たく言えばメンバーシップ関数を作ればいいのです。
分解定理
$$
\mu_A(x)=\displaystyle\sup_{\alpha\in[0,1]}\Bigl[\min\bigl(\alpha,\chi_{A^{\geq\alpha}}(x)\bigr)\Bigr],x\in U
$$
なかなか式が込み入っていますね。
ここで$${\chi_B(x)}$$はメンバーシップ関数の中でも普通の集合(クリスプ集合)に用いられる、「$${x}$$が$${B}$$の要素なら1,要素でないなら0」という関数で、特性関数といいます。
つまり、 $${\chi_{A^{\geq\alpha}}(x)}$$は $${\alpha}$$カットの元でのみ1,そうでなければ0を返す関数です。
$$
\min\bigl(\alpha,\chi_{A^{\geq\alpha}}(x)\bigr)
$$
はつまり、ある$${\alpha}$$のとき、元$${p}$$に対し、$${\mu_A(p)\geq\alpha}$$なら $${\alpha}$$を、$${\mu_A(p)<\alpha}$$なら0を返す操作になります。
これを各$${\alpha}$$ごとに比較し、一番大きいものを採用するのが$${\sup}$$の操作になります。
メンバーシップ関数の値を決めるという行為を$${\alpha}$$カットを決めておく、という行為に落とし込んでいるわけです。
これだけ見ると何言っているのかさっぱりわからん。
こういうのは試しにやってしまうのが一番です。
今、先に $${\alpha}$$を0.1とします。この時、$${\alpha=0.1}$$カットの元が1から2の実数だったとすると、
$$
\chi_{A^{\geq0.1}}(x)=\begin{cases}1&(1\leq x\leq2)\\0&その他\end{cases}
$$
ですから、
$$
\min\bigl(0.1,\chi_{A^{\geq0.1}}(x)\bigr)=\begin{cases}0.1&(1\leq x\leq2)\\0&その他\end{cases}
$$
となります。これで$${\alpha=0.1}$$の段が作れました。
つぎはちょっと大きな$${\alpha}$$で同じことをします。いくらか厳密にやるなら$${\alpha=0.1+\delta,(\delta>0)}$$とでもすべきなんでしょうけど、面倒なんで$${0.11}$$としておきます。
この0.11カットの元が1.1から1.9だとします。すると、
$$
\min\bigl(0.11,\chi_{A^{\geq0.11}}(x)\bigr)=\begin{cases}0.11&(1.1\leq x\leq1.9)\\0&その他\end{cases}
$$
となります。以上二つをひとまずグラフに書いてみると、

となります。
さて、本来はこのまま他の$${\alpha}$$についても計算とカット範囲の策定をする必要がありますが、ひとまずやることのイメージを掴むために、$${\alpha=0.1,0.11}$$のみで次のステップを確認します。次は$${\sup}$$をとるんですね、
これは各$${x}$$ごとに最も大きい $${\alpha}$$を探索することに相当します。
これを行うと、$${1.1< x< 1.9}$$の区間は0.11を取ることになりますし、 $${1< x<1.1,1.9< x<2}$$は0.1を取る関数ができます。
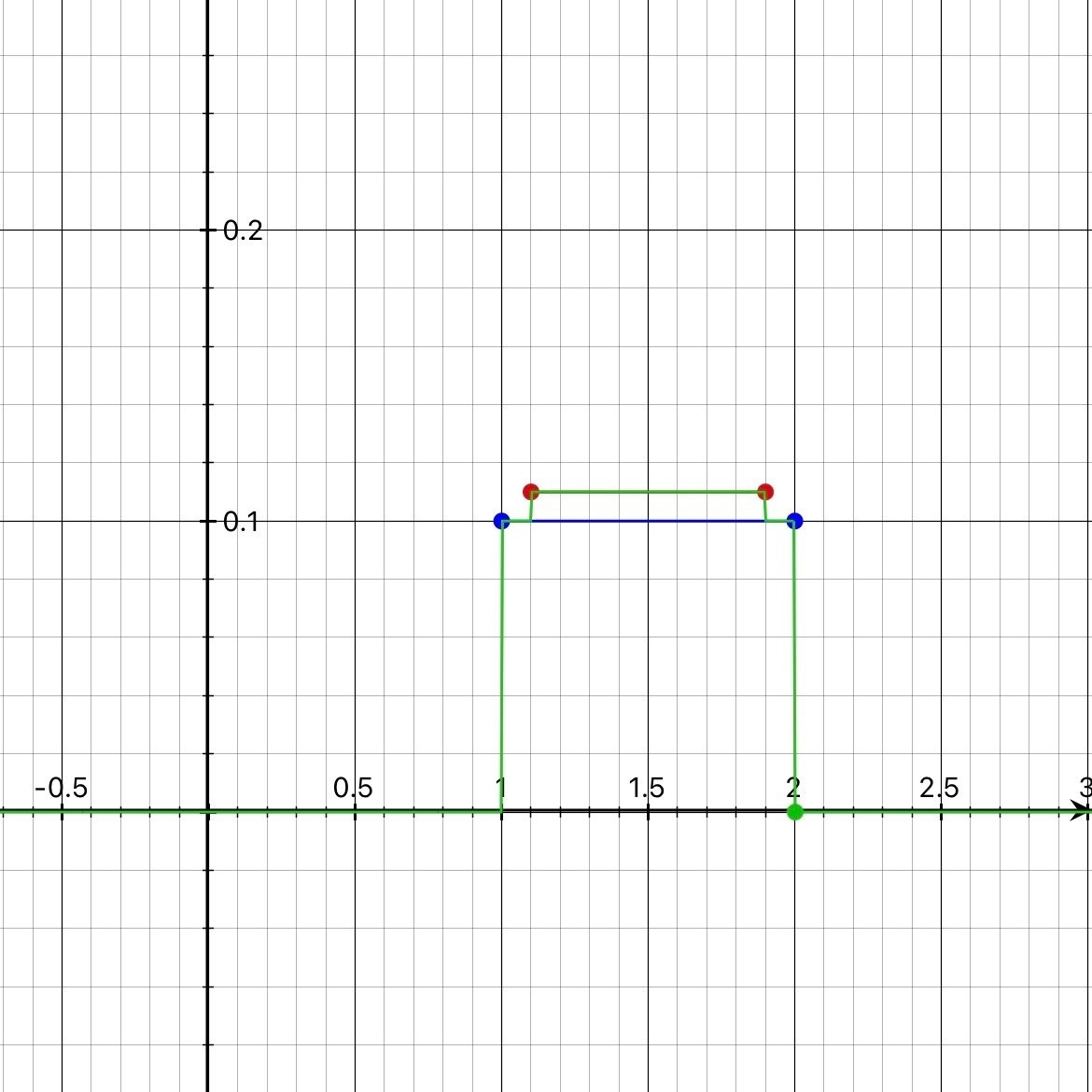
緑の線のようになります。
これを無限に小さい$${\alpha}$$のステップで繰り返せば、たしかに連続的なメンバーシップ関数が作れそうです。
そーやってすぐ物理屋は無限をとるんだから、もう。
以上からクリスプ集合(とその特性関数)と、min,supといった大小関係さえあればメンバーシップ関数が定義できるということです。
これ、本筋とはあまり関係ありませんが、個人的に面白いなと思ってます。
というのも、このminを取る箇所、別にminで書かなくてもいいような気がするんです。というのも、
$$
\alpha\times\chi_{A^{\geq\alpha}}(x)
$$
こんな感じで特性関数とカットレベル$${\alpha}$$の積で表現しても同じことができるわけです。
ところが、わざわざminでやっている。なんでだろうと色々考えたんですけど、一つ思い当たったのは「和や積でよりより根本的な演算が比較」ということかなと思います。言い方が良いかはともかくとして、より原始的と言いますか。
次項でみますが、ファジィ集合で書かれた数同士の演算結果にメンバーシップ関数をどう定義してやるか、そのやり方が分解定理にどことなく似てるんですよね。
たしかにここでいう和や差は元の間の演算で、メンバーシップ関数の演算とは異なる意味の話なのです。でも、例え適用範囲が違っても、気持ち的に和や差を作る前に積を使ってその中身を書くのは、どこか気が進まない気もします。
そういう四則演算抜きに構築して、その上で四則演算を作った方が構築の一貫性はあるんじゃないかなぁ。考えすぎ?
さて、いよいよファジィな数字同士の曖昧な足し算をしていこうと思います。
その前に、ファジィな数とは何かをちゃんと決めておきましょう。
ファジィ数とは
凸ファジィ集合かつ正規ファジィ集合で、連続または区分的連続かつ、少なくとも一点で$${\mu_A(x)=1}$$となるメンバーシップ関数を持つファジィ集合。
なんだか回りくどいですね。
正規かつ凸ならピーク一つだけで、その高さは1のはずです。とはいえ、台形みたいなメンバーシップ関数もあり得ますから、「少なくとも一点で」という制約文がつくのでしょうね。
もし台形みたいにメンバーシップ関数$${=}$$1となる区間がある場合、その区間はfuzzy intervalと呼びます。ファジィ間隔とでも訳すべきでしょうか。
我々がファジィ数として考えることの多くは「10くらい」のようにどこか一点を基準にしていることが多いので、このNoteではfuzzy intervalをもつファジィ数は基本的に扱わないことにします。
区分的に連続でも良いので、無理に正規分布を持ってくる必要もありません。三角形状に上がって下がって、そんな山形の関数、テント関数とかハット関数とも言うようですが、これで考えても良いわけです。

でも微分できる分布はちょっと惹かれますよね。
さて、いよいよ演算です。ただ、いきなり演算をするというより、二項演算後どうメンバーシップ関数を決めるか、まず考えます。
そこで用いるのが拡張原理(Extension principle)です。
$$
\mu_{A\circ B}(z)=\displaystyle\sup_{\alpha}\Bigl[\min\bigl(\mu_A(x),\mu_B(y)\bigr)\Bigr],\;(x,y)\in f^{-1}(z)
$$
こういうのをsup-min合成とも呼ぶようです。
これもまたなかなか複雑そうな式ですね……。どういうことをするかというと、まず演算$${z=f(x,y)}$$は普通に計算してしまいます。
ただし、結果である$${z}$$ごとにメンバーシップ関数を作りたいので、$${z}$$を作るのに使った全ての$${(x,y)}$$について$${\alpha}$$を比較、supを求めていきます。そういうわけで$${(x,y)=f^{-1}(z)}$$という表記がされているのです。
7/16追記。
sup-min合成の式、$${\displaystyle\sup_{(x,y)=f^{-1}(z)}}$$がなんだか$${(x,y)}$$の上限を見ているかのようでわかりにくかったので$${\displaystyle\sup_{\alpha}}$$に書き換えました。
同時に
$${z}$$を作るのに使った全ての$${(x,y)}$$について$${\alpha}$$を比較、supを求めていきます。
と加筆しています。
さてさて、まあこればっかりはやるのが早い。
とはいえ結果$${z}$$になる組$${(x,y)}$$を連続変数で考えるのはあまりに面倒なので、例では離散的な場合を考えましょうか。
まず「2ぐらいの数」を
$$
\begin{matrix}0&1&2&3&4\\0.2&0.5&1&0.5&0.2\end{matrix}
$$
とします。上段が元、下段がメンバーシップ関数の値です。このほかの元では0とします。
同様に「6ぐらいの数」を、
$$
\begin{matrix}4&5&6&7&8\\0.4&0.8&1&0.8&0.4\end{matrix}
$$
とします。
この時の和は、正しい結果ですと$${2+6=8}$$ですから、まずはこれを見ます。
・$${z=8}$$の場合
$$
\begin{matrix}z=x+y&0+8&1+7&2+6&3+5&4+4\\\mu_2(x),\mu_6(y)&0.2,0.4&0.5,0.8&1,1&0.5,0.8&0.2,0.4\\\minの結果&0.2&0.5&1&0.5&0.2\end{matrix}
$$
これで結果8となる組が全て出ました。
この結果のsup、ようはmaxを探すと、$${2+6}$$から作られる8でのmin演算結果が1で最大です。
よって結果8となるメンバーシップ関数の値を$${\mu_{2+6}(8)=1}$$と定義します。
同様のことをほかの結果$${z}$$でもやります。うわっ、めんどくさっ。

こんな感じになります。コンピューターって便利だね。
こういうわけで、めでたく「およそ2」$${+}$$「およそ6」が「およそ8」であることがわかりました。
さて、以上のようにファジィ数の足し算が作れましたから、同じ容量でほかの四則演算も作れそうです。
作れそうなんだけど、これいちいちやるのはなかなか面倒です。
実はもう少し楽にやるやり方があるのですが、それはまた次回としましょう。
お話としては、拡張原理と分解定理がなんとなく似ているなぁって話も掘り下げてみたいところです。
そういうわけでまた次回。
この記事が気に入ったらサポートをしてみませんか?
