トロピカルな計算練習(14)
夏の気配は遠のいて。いよいよ季節は秋に。
今年も海外旅行は厳しかったあなた。
みんな一緒にトロピカルな世界に出かけてみませんか。
常夏の沼にようこそ。
前回はこちら。
トロピカルな二変数関数は、その折れる線に特徴が現れる。
だからトロピカルカーブなんて呼ばれる。
そんなことをやりまして、前回はいろんなトロピカルカーブを描いてみました。

ときに、このトロピカルカーブ、その形から「結晶」とも呼ばれるようです。
「結晶」という呼び方は他の分野とも繋がっているようで、まだまだ掘ると深いですね、トロピカル沼。
さて、このトロピカルカーブなんですけど、$${n}$$次のトロピカルカーブと$${m}$$次のトロピカルカーブの交点の数は(重複度を加味して)$${mn}$$個になります。
普通の関数のグラフでは$${n}$$次の関数からなるグラフ$${m}$$次の関数からなるグラフの交点の数は「重複度」「複素数解」まで含めると$${mn}$$個になります。
これはべズー(Bézout)の定理と呼ばれるもので、一番身近なところだと「直線V.S.二次関数」あの高校の数学Iに出てくるものの一般化になっています。
数学IIIまで行って二次曲線やると、4交点の場合もやれますね。
ともかく、グラフの状況と数式からの解が関連するという、「代数」と「幾何」の接点を強く感じさせられるところですね。
ともかく、トロピカルカーブにおいてもこのべズーの定理が成り立ちます。
例えば

この二つの交点を考えると、
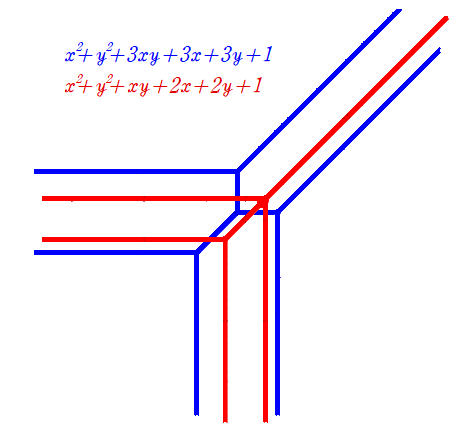


このようにちゃんと4点あります。
ところが

これは3点です。
つまりどこかが重複度を持つということです。
トロピカルなべズーの定理も交点の重複度を考えなきゃいけないんですが、これがどうもパターンがいろいろあるようで面倒そうです。
どういうパターンがあるかというと、先にも触れたように$${m}$$次の多項式と言った場合$${m}$$以下の項が全てあるとは限りません。
$${m}$$次以下全ての項がいる場合といない場合で扱いが異なるわけです。
前者はgenericなトロピカル多項式と呼ばれて区別されています。
ひとまずこのnoteでは簡単な場合として、全ての項がちゃんと出てくる場合(generic)を説明することにします。
ちなみに、そうでない場合、つまり全項いないような場合は無限遠にて交点をもつとして考えるようです。
というのも、項が足りない$${=}$$トロピカルカーブが足りない、という状況ですので、本来あるはずの交点が "そもそも線がない" せいで単純にべズーの定理を使っても数が足りなくなるのです。
ここで$${x,y}$$それぞれの無限遠と$${(-\infty,-\infty)}$$の無限遠を付け加えると、無限遠でトロピカルカーブは出会うと言えるわけです。
そんなのアリかよって思うかもしれませんが、例えば$${x^2+4}$$と$${x^2}$$の交点はどこにもありません。
イメージとしては同じような状況です。
genericではないべズーの定理の扱い、詳しくは名古屋大の代数幾何学勉強会、梶原さんの「トロピカル幾何入門」に載ってます。
genericな場合の重複度をどう定義するかの前に、それぞれのカーブ(交線)にウェイトを定義します。
このウェイトをもって交点の重複度を決めるわけです。
ウェイトはそのカーブ(交線)が何次の面から導かれたかで決まります。
例えば$${1x^2,2x^1}$$から作られた交線は、
$${\begin{pmatrix}2\\0\end{pmatrix}-\begin{pmatrix}1\\0\end{pmatrix}=\begin{pmatrix}1\\0\end{pmatrix}=1\begin{pmatrix}1\\0\end{pmatrix}}$$
より1ですし、
$${1x^2,1y^2}$$からなる交線では、
$${\begin{pmatrix}2\\0\end{pmatrix}-\begin{pmatrix}0\\2\end{pmatrix}=\begin{pmatrix}2\\-2\end{pmatrix}=2\begin{pmatrix}1\\-1\end{pmatrix}}$$
から2となります。
まとめると、$${ax^my^n,bx^py^q}$$では、
$$
\begin{array}{}\begin{pmatrix}m\\n\end{pmatrix}-\begin{pmatrix}p\\q\end{pmatrix}&=&\begin{pmatrix}m-p\\n-q\end{pmatrix}\\&=&\gcd(m-p,n-q){\bf k}\\&=&w{\bf k}\\\\w&:=&\gcd(m-p,n-q)\end{array}
$$
ここで$${w}$$はウェイト、$${{\bf k}}$$はprimitive vectorです。primitive vectorはいわゆる基底ベクトルとは違うものです。
例えば$${\begin{pmatrix}2\\1\end{pmatrix}}$$なんかもprimitive vectorになります。
で、このprimitive vectorはプラマイの不定性はありますが、トロピカルカーブに対して垂直になります。
一応確かめることにします。
例えば$${ax^my^n,bx^py^q}$$の交線$${mx+ny+a=px+qy+b}$$より、
$$
(m-p)x+(n-q)y+(a-b)=0
$$
ですから、この方向ベクトルは$${\bigl(n-q,-(m-p)\bigr)}$$になります。
こうしてprimitive vectorがトロピカルカーブと直交しているとわかります。
先ほどの例の場合だと、

面の構成が上のようになっているので、

このようになります。
で、このウェイトとprimitive vectorを使って、交点の重複度は
$$
d=w_iw_j \left|\det\left[{\bf k}_i,{\bf k}_j\right]\right|
$$
で決まります。
例えば$${1x^2,2x^1}$$から作られた交線と$${1x^2,1y^2}$$からなる交線では、各々ウェイトとprimitive vectorが
$$
\begin{array}{}1,\begin{pmatrix}1\\0\end{pmatrix},\;\;\;\:2,\begin{pmatrix}1\\-1\end{pmatrix}\end{array}
$$
より、
$$
d=1\times2\left|\det\begin{bmatrix}1&1\\0&-1\end{bmatrix}\right|=2
$$
となるわけです。
先ほどの例でいうと、

となるため、$${1+1+2=4}$$となるわけです。
ここで出てきたprimitive vectorの利用例として、釣り合い条件(balanced condition)を紹介しておきましょう。
釣り合い条件とは、トロピカルカーブ上の結節点について成り立つ式です。
カーブを構成する線のウェイト$${w_i}$$とprimitive vectorを$${{\bf v}_i}$$とすると、
$$
\displaystyle\sum_iw_i{\bf v}_i=0
$$
が成り立ちます。
なるほと、たしかに釣り合いの式です。物理っぽいですね。
ところで、トロピカルカーブの式はベクトルを用いても導けます。
まあ、わざわざベクトルでやる理由もないわけですけど、所々ウェイトの定義で出てきた形が出てくるので興味深いところでもあります。
まず項$${tp(ax^sy^t)}$$を考えます。
これは普通の計算でいうと、$${sx+ty+a}$$です。
この平面の式に対し法線ベクトルをつくります。
$$
\begin{array}{}(x,y)&=&(0,0)&\Rightarrow& (0,0,a)\\(x,y)&=&(1,0)&\Rightarrow& (1,0,s+a)\\(x,y)&=&(0,1)&\Rightarrow& (0,1,t+a)\end{array}
$$
こうして3点が決まるので、ここから2本のベクトルをつくります。
$$
\begin{array}{}(1,0,s),(0,1,t)\end{array}
$$
で、こいつをウニャウニャやれば法線ベクトルになるんですが、面倒なんで外積を使います。
$$
\begin{pmatrix}1\\0\\s\end{pmatrix}\times\begin{pmatrix}0\\1\\t\end{pmatrix}=\begin{pmatrix}-s\\-t\\1\end{pmatrix}
$$
外積って便利ですね。
ここで、ベクトルは別に正負なんて係数でなんともできます。そこで係数として$${-1}$$を取り除いてやります。
$$
\begin{pmatrix}s\\t\\-1\end{pmatrix}
$$
こいつの$${x,y}$$方向は、ウェイトの定義と同じく、トロピカルな$${x,y}$$の指数になっています。
さて、ここで面を二つ用意しましょう。
項を$${tp(kx^ay^b),tp(lx^cy^d)}$$としますと、各法線ベクトルは、$${(-a,-b,1),(-c,-d,1)}$$です。
この二つの法線ベクトルに垂直なベクトルは交線のベクトルになります。
$$
\begin{pmatrix}-a\\-b\\1\end{pmatrix}\times\begin{pmatrix}-c\\-d\\1\end{pmatrix}=\begin{pmatrix}-b+d\\a-c\\ad-bc\end{pmatrix}
$$
こいつを$${x,y}$$平面に射影させるとトロピカルカーブの方向ベクトルになります。
射影演算は
$$
\begin{pmatrix}1&0&0\\0&1&0\\0&0&0\end{pmatrix}\begin{pmatrix}-b+d\\a-c\\ad-bc\end{pmatrix}
$$
こんな感じでやりますが、ようはベクトルの$${x,y}$$成分だけ抜き出すわけです。
$$
\begin{pmatrix}-b+d\\a-c\end{pmatrix}
$$
で、こいつに垂直な($${x,y}$$平面上の)ベクトルを考えます。
$$
\begin{pmatrix}a-c\\b-d\end{pmatrix}
$$
はい、これ、ちゃんとprimitive vectorになるんですね。
こんなふうにやれると、二変数に限らず多変数のトロピカル多項式まで拡張を考えることもできます。
いずれにしてもトロピカルは初等的な数学でも案外楽しめるのが面白いところです。
沼の辺りで遊ぶだけならね。
この記事が気に入ったらサポートをしてみませんか?
