ファジィ集合のはなし(11)
だいぶ期間があきましたが、こっちも忘れてはいません。
ファジィ集合というのは何か、詳しいことは初回から読んでいただくとして、大雑把にいうと、
・普通の集合(クリスプ集合)は10以上のように含む含まないは二者択一。
・どのくらい含むかを数値化(帰属度)して「どちらともいえない」を許容するのがファジィ集合。
・帰属度はメンバーシップ関数で記述。
・メンバーシップ関数はクリスプ集合である$${\alpha}$$カットから構成できる。(分解定理)
・集合間の演算はsup-min合成から作れる。
という話でした。
今回からはメンバーシップ関数の値までファジィなものにするタイプ2-ファジィ集合を見ていきます。
今回の話に出てくるものは、メンバーシップ関数の値をファジィ化したものです。
つまり、$${A}$$というファジィ集合におけるある元$${a}$$の帰属度$${\mu_A(a)}$$が確定値にはならず、「0.2から0.6の帰属度」のように幅を持つことになります。
で、そのなかでも「帰属度0.4が一番そうだといえるなぁ」ということ。いわば「帰属度の帰属度」ですね。今の場合「帰属度の帰属度」が1になるのが「帰属度0.4」だというわけです。
帰属度の帰属度とは言いにくいので、これのことをファジィ帰属度と呼びます。
一方、今までのノーマルな帰属度は数値帰属度などと呼ばれます。

横軸が数値帰属度で、縦軸がファジィ帰属度です。
さまざまな元に対してこのようなグラフが付随するのですから、タイプ2ファジィのメンバーシップ関数は、

三次元で書くことになります。
緑軸が元を、青軸が数値帰属度を。赤軸がファジィ帰属度です。
黄色で書かれている断面が先ほどの

これだと思ってください。
もちろんメンバーシップ関数の形はこれと限った訳ではありません。
こういう様子をわかりやすく書こうと思うと、断面のスライスを書くしかありません。
あとはよく見る図だと、

この方向の投影図でみる機会が多い気がします。
この投影図で見ると、どの元で数値帰属度がどういう範囲にあるか把握し易いんでしょう。
こういう図をFOU(Footprint of uncertainty:直訳すると不確実性の足跡)といいます。
また、緑の線はファジィ帰属度が1の部分ですから、これがタイプ1-ファジィ集合、つまり今まで見てきたファジィ集合というわけです。

例えばこの場合FOUは青い領域です。
先述の例同様元が2で帰属度が最大値になる場合ですが、その帰属度は1と確定したわけではなく、ある程度の幅が見込まれているとわかります。
またこの例でのFOUの上下の境界線、図の赤と緑の線はそれぞれUMF,LMF(Upper/Lower Membership Function)といいます。
ところでこのタイプ2-ファジィのメンバーシップ関数、どう表記したものか実に悩まされてます。
普通こういうのは二変数関数だし、数値帰属度$${\mu}$$、ファジィ帰属度$${\nu}$$として、$${\mu(x,\nu)}$$みたいなものだろうと言いたいのです。
しかし、元$${x}$$があった時$${\mu_x(\nu)}$$なるグラフが得られる、というのがやりたいことに近いような気がします。
つまりあくまで第一の変数は$${x}$$であると。
これは気持ちの問題ですが、どうも$${\mu(x,\nu)}$$だと$${x}$$と$${\nu}$$が対等に見えてしまいます。
一つの解決策としては、$${\mu(x;\nu)}$$と明らかに分けて表記することかなぁと思います。
さて、では今度はタイプ2-ファジィ集合どうしの集合演算を考えます。
いままでの(タイプ1-)ファジィ集合ではメンバーシップ関数のmaxやminを取ることで和集合や共通部分を取ってきました。
しかし今回はそんな簡単にはできません。
そもそも(タイプ1-)ファジィ集合ではあまり気にかけずにmax,minを取っていましたが、あれは暗黙のうちに「同じ元に対する帰属度の比較」をしていました。
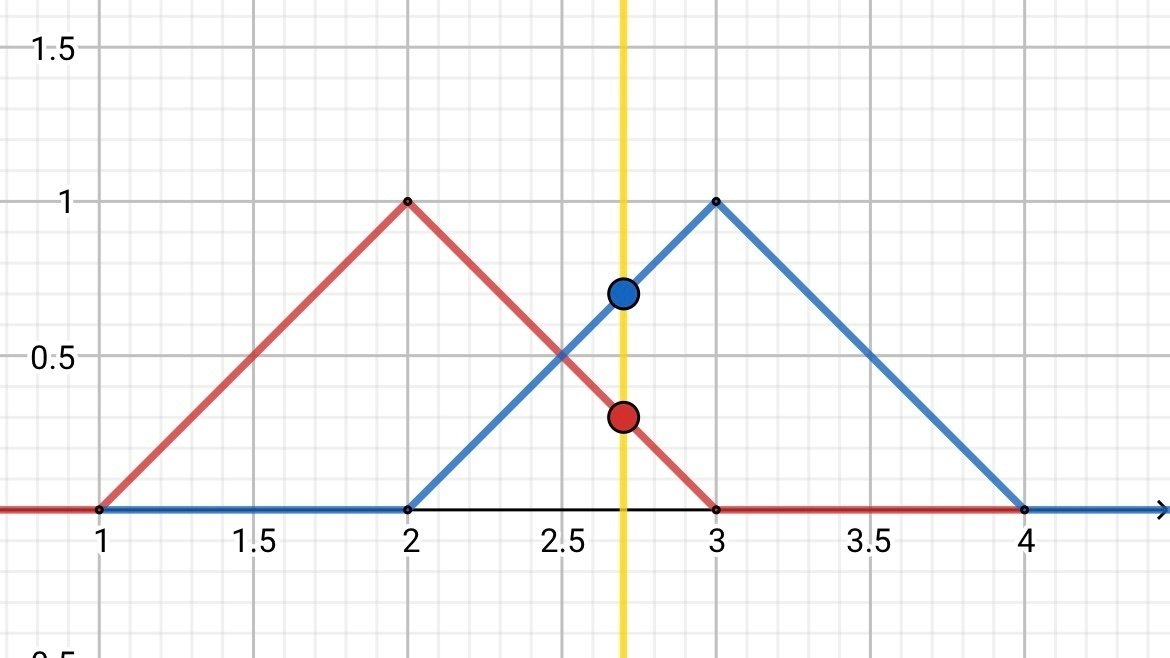
今回タイプ2ではファジィ帰属度がいるせいで比較できるほど条件が定まっていない、緩い状況にあります。
ある元で三次元にわたるメンバーシップ関数の断面を取ると、たとえば、

こんな感じで、いま縦軸が数値帰属度、横軸がファジィ帰属度です。
つまり、今までの(タイプ1-)ファジィ集合ではファジィ所属度$${=1}$$の点。図での緑の二つの点を比較していたわけです。
この自然な拡張を考えるなら何らかの方法でファジィ所属度ごとのスライスをさらにして、数値帰属度の大小を測るべきでしょう。
そして出てきた結果は再びタイプ2-ファジィ集合になるはずですから、演算そのものに区間の要素があるべきです。
何だかごちゃごちゃ言っていますが、要するに(タイプ1-)ファジィ集合で四則演算を入れた時と同じことを考えればいいんです。
拡張原理か区間演算で集合演算を定義します。
拡張原理って何だったっけという方は以下を参照。
ただし、拡張原理は非常に計算が面倒でした。
$$
\begin{array}{}\mu_{A\circ B}(z)=\sup\bigl[\min(\mu_A(x),\mu_B(y))\bigr],(x,y)=f^{-1}(z)\end{array}
$$
具体的には
1.先に結果$${z}$$を決めて
2.逆関数からその結果$${z}$$になる元の組$${(x,y)}$$を全て求め
3.$${x,y}$$のそれぞれのメンバーシップ関数での所属度を求めその小さい方を記録し
4.全ての組における記録値の中で最大(上限)を演算結果の所属度とする
というものでした。
これに対して区間演算のやり方は凸なファジィ集合(変にメンバーシップ関数が凸凹してない)にしか適用できませんが、手っ取り早く答えを出してくれるものです。
これは、
1.ある所属度$${\alpha}$$に注目する。
2.所属度が$${\alpha}$$である最大と最小の$${x,y}$$を記録する。$${(x_L,x_G,y_L,y_G)}$$
3.実際に演算を$${(x_L,x_G,y_L,y_G)}$$から4パターンやってみる。
4.結果一番小さくなった$${z}$$と大きくなった$${z}$$が求める$${\alpha}$$カットの区間。
というものです。
タイプ2の場合、まず元を設定してそこから得られるファジィ所属度$${(\nu)}$$v.s.数値所属度$${(\mu)}$$のグラフ、これはタイプ1のメンバーシップ関数になってますので、これを区間演算に入れることになります。
ということはつまり、この「元における断面」として得られる二つのタイプ1のメンバーシップ関数のうち、一番外側(区間の両端)の$${\nu}$$を探していき、得られた計四つの両端から所定のmaxなりminなりの演算をすることになります。
図で考えてみることにします。
まず上の状況の再掲です。これは適当な二つの元でのファジィ所属度グラフを見ているということです。

いま、二つの集合のmin演算を考えます。
まず下端を考えます。それぞれのファジィ所属度グラフの下端は図の実線(太線含む)です。
この二つを比較してより低い所属度をもつ部分を太線にしました。

続いて今度は上端を見ましょう。
下端はもう決まったので黄色く塗りました。

この二つのうち小さい方を取ることになります。
ここで注意ですが、maxをとるのではありません。
というのも、我々は今二つの集合のmin演算をしているわけです。
より大きい方を取るというのが目的ではありません。
今の場合ですと、赤線の方が低いので、これが結果になります。
よって得られる演算後のファジィ所属度は

このような黄色い線になります。
交点で折れるのがミソです。
同じことをmax演算の場合でやると以下の緑の線のようになります。

念のため記しておくと、それぞれの線は元々の元から以下のように構成されています。

以上から、ある元におけるファジィ所属度と所属どの関係がわかるので、あとはいろいろな元について同じことをすれば、タイプ2-ファジィ集合における和集合(max),共通部分(min)がもとまるというわけです。
さて、和集合と共通部分ができましたので、あとは補集合を考えます。
タイプ1-ファジィ集合の場合、補集合はもとのメンバーシップ関数$${\mu_A}$$に対して、
$$
\mu_{\bar{A}}=1-\mu_A
$$
で決めるものでした。
ならばタイプ2-ファジィ集合の場合も上端下端を用意して1から引くことで補集合の区間を定義できそうです。

いま、ファジィ所属度が青い線(と点線)で書かれる時、補集合のファジィ所属度は緑の線と点線になります。
実線は実線どうし、点線は点線どうしで対応しています。
これをみると0.5について対称であることがわかります。
そういえばタイプ1でもそうでしたね。
以上の区間演算を行う際に本当は注意しないといけないことがあります。
というのも区間演算の復習で簡単に触れましたが、区間演算は凸なファジィ集合にしか使えないのです。
つまり今上で扱ったファジィ所属度v.s.数値所属度のグラフも区間演算で考えたければ凸ファジィ集合でないといけないということです。

こういうのはダメというわけです。
最初に挙げた3次元の図も凸ファジィ集合になるようにしていましたが、一般の場合を考えるとやっぱり区間演算は拡張原理には劣ってしまうわけです。
とはいえ応用では「そもそも2つコブのあるようなメンバーシップ関数なんて使わなければいいじゃん」と先手を打てるので、都合の良いところは真似するのスタンスで、本稿では断面も凸ファジィ集合になるようなメンバーシップ関数しか扱わないことにします。
さて、今回はタイプ2-ファジィ集合の導入でした。
演算でどんなことがわかるかは次回見ていきます。
