ファジィ集合のはなし(3)
前回は和集合や共通部分をファジィ集合に導入してみました。
詳細は前回の記事を見てもらうとして、ようはメンバーシップ関数の関係式にしてしまえば良いということです。
で、前回は差集合の話をし始めたところで、ド・モルガンも確認しておくべきだな、となったわけです。
ド・モルガンの法則は
$$
\begin{array}{}(A\cap B)^c=A^c\cup B^c&,&\overline{A\cap B}=\overline{A}\cup \overline{B}\\(A\cup B)^c=A^c\cap B^c&,&\overline{A\cup B}=\overline{A}\cap \overline{B}\\\end{array}
$$
はい。前回お話ししたように、ファジィ集合では文字の頭の上が混雑するので、補集合は基本的に$${A^c}$$の形式で書くことにします。
ただ、このノート、万が一高校生が読んでいるとかわいそうですから、毎回記法はことわって置くことにします。
こういうのは紙の本でやると大変な心遣いですから、Web上でこそですね。
むかし、もう少しやる気のあった頃、式の等号にマウスを置くと具体的な式変形が表示される解説サイトをやろうと思ったんですが、他のことに感けてて結局やらずじまいでした。
今始めてもなんだかんだ需要はあるんじゃないかなと思うんですが、どなたかやってみません?
ファジィでの確認は、ルールに基づいてメンバーシップ関数をいじっていけばできます。
煩雑になるんで、$${\mu_{\tilde{A}}(x)}$$の変数$${x}$$(全体集合$${X}$$について $${x\in X}$$)は省略します。
$$
\begin{array}{}(\tilde{A}\cap\tilde{B})^c&=&1-\min(\mu_{\tilde{A}},\mu_{\tilde{B}})\\\tilde{A}^c\cup\tilde{B}^c&=&\max(1-\mu_{\tilde{A}},1-\mu_{\tilde{B}})\\&=&1+\max(-\mu_{\tilde{A}},-\mu_{\tilde{B}})\\&=&1-\min(\mu_{\tilde{A}},\mu_{\tilde{B}})\end{array}
$$
となります。ちょっと最後の変形が一見しただけでは追いにくいのですが、場合分けすれば示せます。
$$
\begin{array}{}a< b,&\max(-a,-b)=-a=-\min(a,b)\\a>b,&\max(-a,-b)=-b=-\min(a,b)\end{array}
$$
さて、そういうわけでド・モルガンは成立してます。
ことのついでにちょっと忘れてましたけど、補集合の補集合、二重否定のようなものがどうなるか見ましょう。
$$
\begin{array}{}\mu_{\tilde{A}^c}&=&1-\mu_{\tilde{A}}&&\\\mu_{(\tilde{A}^c)^c}&=&1-(1-\mu_{\tilde{A}})&=&\mu_{\tilde{A}}\end{array}
$$
というわけで、$${(\tilde{A}^c)^c=\tilde{A}}$$と言えます。
もういくつか調べておきましょう。
これは有名な話なんですが、ファジィ集合では次のいわゆる矛盾律と排中律が成立しません。
$$
A\cap A^c=\emptyset,\;\;A\cup A^c=U
$$
ここで$${\emptyset}$$は空集合、$${U}$$は全体集合です。
ファジィ集合の概念では、空集合は全ての全体集合の元に対してメンバーシップ関数が0
$$
\mu_{\tilde{\emptyset}}(x)=0,(x\in U)
$$
ですし、全体集合は
$$
\mu_{\tilde{U}}(x)=1,(x\in U)
$$
ですが、ダメなんですね、成り立たない。
しかし、言われてみりゃ当たり前の話で、ファジィ集合なんて1か0かの二者択一以外、曖昧な意見を認めてるんですから、排中律が成り立つ気がしません。
排中律がダメそうなのにド・モルガンが生きてますから、これじゃ自動的に矛盾律も死んでしまいそうだなぁと予想できますね。
$$
\begin{array}{}&A\cap A^c&=&\emptyset\\&(A\cap A^c)^c&=&A^c\cup A\\=&\emptyset^c&=&U\end{array}
$$
こんな感じで等価なわけですから。
具体例でやってみましょうか。
ちょっと極端ですが例えばファジィ集合のメンバーシップ関数として
$$
\mu_{\tilde{A}}(3)=0.5,(全体集合は3のみ)
$$
とします。一個しか元が無い。
すると、
$$
\mu_{\tilde{A}^c}(3)=1-0.5=0.5
$$
ですから、
$$
\begin{array}{}\mu_{\tilde{A}\cup\tilde{B}}=\max(0.5,0.5)=0.5\\\mu_{\tilde{A}\cap\tilde{B}}=\min(0.5,0.5)=0.5\end{array}
$$
となってしまい、やっぱり全体集合や空集合にはなりません。
さて、こうなってくると分配法則もチェックしておきたくなります。
集合で分配法則? って思う人もいるかもしれませんが、複数の演算があるなら分配法則は確かめたくなるもんです。
$$
\begin{array}{}A\cap(B\cup C)&=&(A\cap B)\cup(A\cap C)\\A\cup(B\cap C)&=&(A\cup B)\cap(A\cup C)\end{array}
$$
これをメンバーシップ関数の間の関係に直すと、以下を示すことになります。
いちいち$${\tilde}$$を打つのが面倒なので、省略させていただきますと、
$$
\begin{array}{}\min\Bigl(\mu_A,\max(\mu_B,\mu_C)\Bigr)&\overset{?}{=}&\max\Bigl(\min(\mu_A,\mu_B),\min(\mu_A,\mu_C)\Bigr)\\\max\Bigl(\mu_A,\min(\mu_B,\mu_C)\Bigr)&\overset{?}{=}&\min\Bigl(\max(\mu_A,\mu_B),\max(\mu_A,\mu_C)\Bigr)\end{array}
$$
これを示すには、ある元$${x}$$でメンバーシップ関数の大小がどうなっているか考えるのが手っ取り早そうです。もう$${\mu}$$すら書くのが面倒くさいので、添字だけ書きます。
とりあえず一つ目の式の結果は、
$$
\begin{array}{}大小&左辺&右辺\\A< B< C &A&A\\A< C< B &A&A\\B< C< A &C&C\\B< A< C &A&A\\C< A< B &A&A\\C< B< A &B&B\end{array}
$$
とまあ、うまく成立しているわけです。
一つ目の式が大丈夫なら、二つ目の式も大丈夫でしょう、きっと。
それに考えてみるとこれは、拙稿「エキゾチック演算遊び(8:第二脱量子化)」でやっているものとおなじです。
さて、いよいよ差集合ですが、
$$
\begin{array}{}A\setminus B&=&A\cap (A\cap B)^c\\&=&A\cap(A^c\cup B^c)\\&=&(A\cap A^c)\cup(A\cap B^c)\\&=&\emptyset\cup(A\cap B^c)\\&=&A\cap B^c\end{array}
$$
この2行目と5行目、どちらを差集合にするか悩ましいんです。この二つがちゃんと一致すれば良いんですが、途中に$${A\cap A^c=\emptyset}$$をつかってしまっています。
実際適当なメンバーシップ関数で二行目の式と五行目の式を書くと一致しないことがわかります。
以下のグラフは$${e^{-x^2},e^{-(x-1)^2}}$$から二行目(緑)と五行目(黄)を求め、見やすいよう$${y}$$軸方向にずらしたものです。
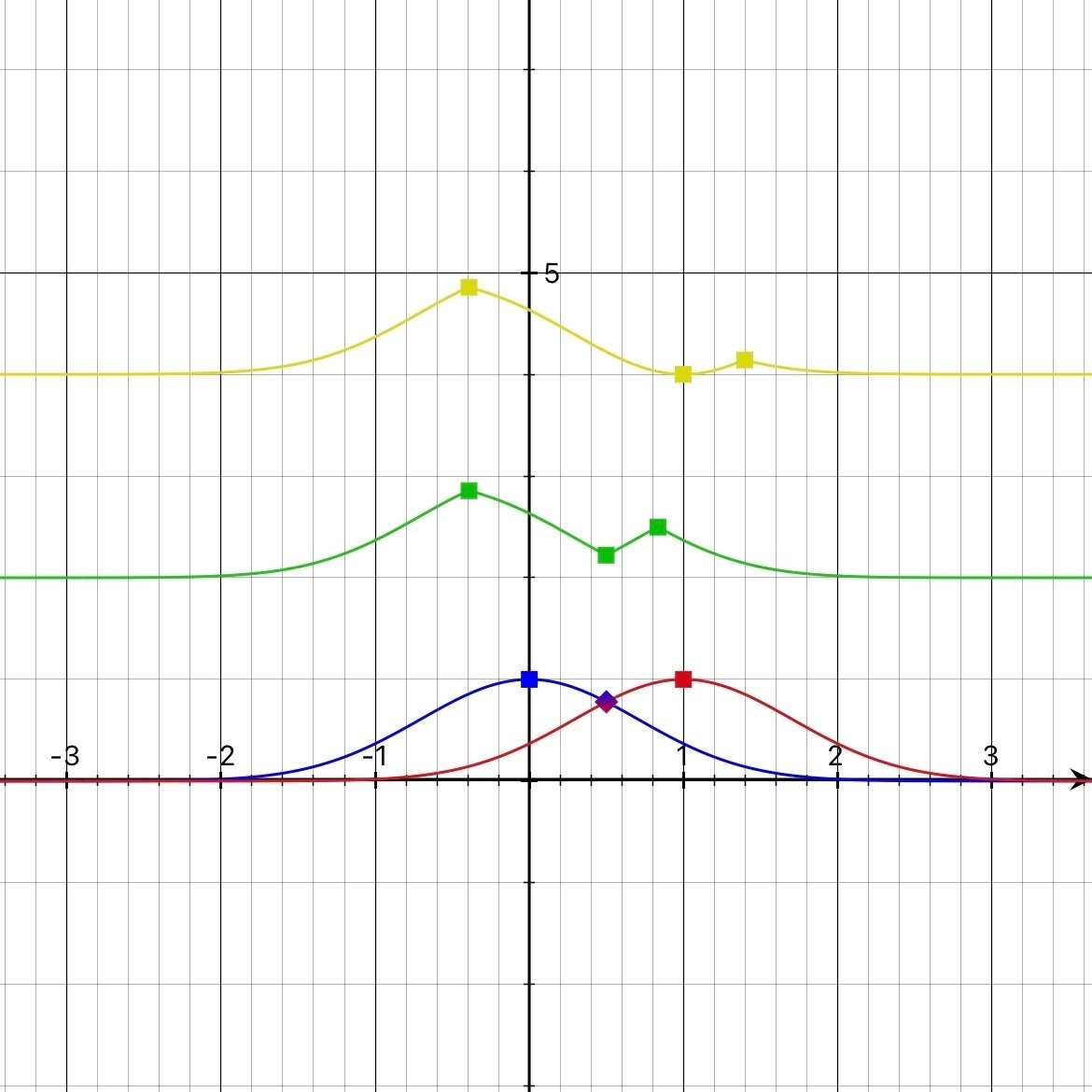
つまり、0ぐらいの数から1ぐらいの数の集合を引いたイメージ、つまり「0ぐらいの数にしたいけど、1ぐらいの数は外したいメンバーシップ関数」なんですね。
気をつけなきゃいけないのは、差集合は決して初等代数的な引き算とは違うので$${-1}$$ぐらいの数を言いたいわけではありません。
そういうファジィな足し算引き算はまた回をあらためてお話しします。
そうなると、メンバーシップ関数の立場からしたら、$${x=1}$$で0になる定義の方がやりたいことにはかなっていそうです。
実際、ファジィ集合をはじめたザデー(Zadeh)も差集合に関しては私が五行目に書いた演算を定義として用いています。
なので余計な不安などあおらず最初から$${\tilde{A}\setminus \tilde{B}=\tilde{A}\cap \tilde{B}^c}$$とすればよかったんですね。
めでたしめでたし。
さて、今回でファジィ集合の通常の集合っぽい部分はチェックできたので、次回からはファジィ集合特有の部分を掘り下げていこうと思います。
この記事が気に入ったらサポートをしてみませんか?
