
デモクリトスはかく語りき-原子論の世界観-
序.
問題】円錐を平面でスパッと切断したときの断面A(上側)とB(下側)の面積はどちらが大きいか?
— 古代ギリシャのアライさん (@kodaigirisyano) August 7, 2021
お気軽に投票くださいなのだ!
↓画像もご確認ください.

本noteでは,この問題をごく簡単に検討してみます.(2021 8/12,誤植があったので訂正しました.)
1. 同じ?
投票の結果,断面AとBの面積は等しいという意見が圧倒的に多数でした.切断前はぴったり同じものだったのですから,この意見は説得的にみえます.
ですが次のように考えるとどうでしょうか?
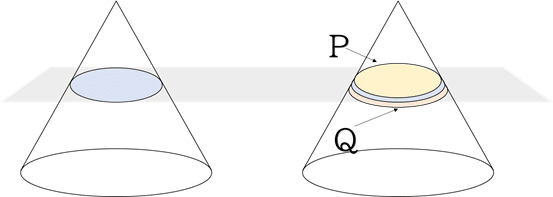
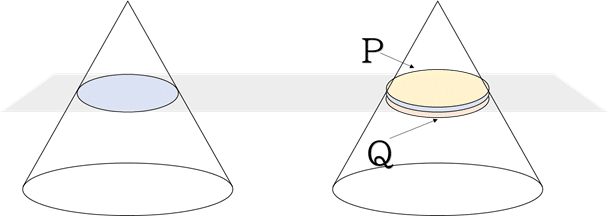
断面の少し上,もしくは下を同じくスライスします.それをPとQとします.すると断面の大きさは
P<A=B<Q
となります.
ここでPとQの距離を限りなく近づけていくとどうなるでしょうか?
0になるギリギリまで近づけると,Q=A=B=Pとなるのでしょうか?
すると,どこを切断しても断面積は同じという結論になってしまいます.
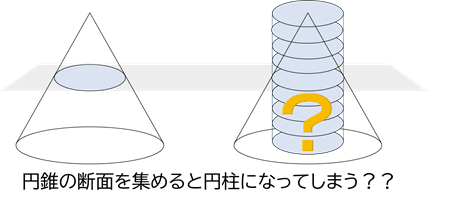
これは困りました.
2. 違う?
それではAとBの大きさは異なるのか?すると円錐は拡大してみると階段状になっているということになります.

これも困った事態です.ところで「現代数学」では,定義や公理を置くことで,このような矛盾は発生しないようになっていますので,この問題は解決済です.

しかし我々の目の前にある円錐が,数学で扱われる円錐と同じということを「数学」は保証してくれません.この世界が,数学の定義や公理で設計されているかどうかは誰も知らないのです.
アポリア(行き詰まり)に陥ったところで,今日の主役デモクリトス(前460年~前370年頃)に登場してもらいましょう.

3.デモクリトスはかく語りき
原子論で有名なデモクリトスは次のように語ったとされます.
デモクリトス「断片」(日下部吉信 訳)
円錐が底面に平行な面で切られたとき,切られた〔二つの〕平面を,どのように考えるべきであろうか.等しくなるであろうか,それとも等しくなくなるであろうか.
等しくないとするなら,円錐は多くの階段状の切り込みとギザギザを得ることとなり,一様でない様相を呈することになろうし,
他方,もし等しいなら,切り口も等しくなるであろう.したがって等しくない円からではなく,等しい円からなることになり,円錐は円柱の様相を呈することになるが,これは極めて不合理である.
難しい表現ですが,円錐が円柱の様相を呈することが「極めて不合理」であるといっています.この言及とデモクリトスが原子論者であったことから,彼は円錐の斜面が階段状になっているという想定をしていると考えられています.
物体は最小単位である「アトム(分割できないという意味のギリシャ語アトモスが語源)」が積み重なって出来上がっていると考えたのです.

それでは,高精度の顕微鏡で円錐を観察すれば,アトムの階段が見えるということでしょうか?

このことについては現代において特に誤解が甚だしいのですが,「理科」で習う原子や元素はデモクリトスの想定した「アトム」とは別物です.アトムは最小単位.素粒子よりも,桁外れに小さいのです.デモクリトスはその「小ささ」について次のように語ります.
デモクリトス「断片」(日下部吉信 訳)
実体はわれわれの感覚では捉えられないほど小さいと彼は考える.
小ささゆえに,人の感覚では決して捉えることが出来ないもの.それがデモクリトスの想定するアトムです.よって我々の感覚では,円錐の斜面は決して階段状には見えないということなります.
おわりに
古代ギリシャでは,デモクリトスとは別に,実体はいくらでも分割できると考えた哲学者もいました(例えばアナクサゴラス).さらにユークリッド(エウクレイデス)『原論』に代表されるギリシャ数学は,無限分割を認める立場で研究されました.本noteの冒頭「1.同じ?」で見た無限分割の矛盾は,彼らの研ぎ澄まされた論理の力で,解決することに一応の成功を収めたのです.
最小単位が存在するのか否かが,何故重大な問題なのか? 我々には想像もできないことですが,ギリシャの哲学者にとっては「知性の在り方」,ひいては「生き方」までを規定する重要な問題だったのです.
最後に古代の思想に関心を持った方にいくつか参考文献をご紹介します.
参考文献
納富信留『ギリシア哲学史』通史としてもっとも重要な文献.
通称クサカベクレスによる,哲学史講義.原子論の説明が秀逸.
ギリシャ数学における無限論を学ぶにはこちら.斎藤憲『アルキメデス「方法」の謎を解く』.数学者の根底に原子論者の思想が受け継がれていたことや,論理の力で無限を制御した方法が学べます.
ギリシャ数学についてのはこちらのnoteも参考にしてください.
終
この記事が気に入ったらサポートをしてみませんか?
