
位相空間、トラジェクトリー
前野昌弘著「よくわかる解析力学」によると『位相空間とポアッソン括弧を使いこなさないならハミルトン形式を使う意味はない』とのことだ。そうなんや。
位相空間(phase space)とは簡単にいえば、一般化座標$${q_i}$$と一般化運動量$${p_i}$$を軸とした空間である。そして、この空間$${(\{q_i\},\{p_i\})}$$内で各瞬間の物体の運動は点で表わされる。時間と共に点がたどる軌跡がトラジェクトリー(trajectory)である。
1 等速度運動
質量$${m}$$の物体が$${q}$$軸上を速度$${\dot{q}}$$で等速度運動をしている。重力等の外力はない。

$${T=\dfrac{1}{2}m\dot{q}^2}$$、$${U=0}$$ よって$${\mathscr{L}=T+U=\dfrac{1}{2}m\dot{q}^2}$$ (L)
$${p=\dfrac{\partial\mathscr{L}}{\partial\dot{q}}=m\dot{q}}$$ よって$${\dot{q}=\dfrac{p}{m}}$$ (q)
$${\mathscr{H}=p\dot{q}-\mathscr{L}=p\dot{q}-\dfrac{1}{2}m\dot{q}^2=p\dfrac{p}{m}-\dfrac{1}{2}m\Big(\dfrac{p}{m}\Big)^2=\dfrac{p^2}{2m}}$$ (H)
$${\dot{q}=\dfrac{dq}{dt}=\dfrac{\partial\mathscr{H}}{\partial p}=\dfrac{p}{m}}$$ (H1) ← (q)と同じ
$${\dot{p}=\dfrac{dp}{dt}=-\dfrac{\partial\mathscr{H}}{\partial q}=0}$$ (H2)
よって
$${q=\dfrac{p}{m}t+C_1}$$ (H1)' $${p=const=C_2}$$ (H2)'
初期条件として$${t=0}$$のとき $${q=q_0, \dot{q}=v_o}$$とすると
(H1)'に代入 $${q_0=C_1}$$ よって $${q=\dfrac{p}{m}t+q_0}$$ (H1)''
(p)より $${p_0=mv_0}$$、よって(H2)'は $${p_0=C_2}$$ $${p=p_0=mv_0}$$ (H2)''
以上より
トラジェクトリーは$${(q_0, v_0m)}$$を起点とする$${q}$$軸に平行な直線である。
$${v_0>0}$$のときは、$${q}$$軸の正の方向に速さ$${p_0=mv_0}$$で移動する。
$${v_0<0}$$のときは、$${q}$$軸の負の方向に速さ$${p_0=mv_0}$$で移動する。
そして、その速度は起点$${(q_0, v_0m)}$$が$${q}$$軸からの距離に比例する。
$${v_0=0}$$のときは、$${q}$$軸上の起点起点$${(q_0, 0)}$$に留まったままである。

2 落下運動
質量$${m}$$の物体が重力により落下する。物体の基準点$${q=0}$$から下方への距離を$${q}$$、速度を$${\dot{q}}$$、重力加速度を$${g}$$とする。

$${T=\dfrac{1}{2}m\dot{q}^2}$$ $${U=\displaystyle\int_0^q(-mg)dq=-mg\Big[ q \Big]_0^q=-mgq}$$
$${\mathscr{L}=T-U=\dfrac{1}{2}m\dot{q}^2+mgq}$$ (L)
$${p=\dfrac{\partial\mathscr{L}}{\partial\dot{q}}=m\dot{q}}$$ よって$${\dot{q}=\dfrac{p}{m}}$$ (q)
$${\mathscr{H}=p\dot{q}-\mathscr{L}=p\dot{q}-\dfrac{1}{2}m\dot{q}^2-mgq=p\dfrac{p}{m}-\dfrac{1}{2}m(\dfrac{p}{m})^2-mgq}$$
$${=\dfrac{p^2}{2m}-mgq}$$ (H)
$${\dot{q}=\dfrac{dq}{dt}=\dfrac{\partial\mathscr{H}}{\partial p}=\dfrac{p}{m}}$$ (H1) ← (q)と同じ
$${\dot{p}=\dfrac{dp}{dt}=-\dfrac{\partial\mathscr{H}}{\partial q}=mg}$$ (H2)
よって
$${q=\dfrac{p}{m}t+C_1}$$ (H1)' $${p=mgt+C_2}$$ (H2)'
初期条件として$${t=0}$$のとき$${q=q_0, \dot{q}=v_o}$$とすると
(H1)'に代入 $${q_0=C_1}$$ よって$${q=\dfrac{p}{m}t+q_0}$$ (H1)''
(p)より$${p_0=mv_0}$$、よって(H2)'は$${mv_0=C_2}$$ $${p=mgt+mv_0}$$ (H2)''
(H2)''に(q)を代入 $${m\dot{q}=mgt+mv_0}$$ $${\dot{q}=gt+v_0}$$
積分して$${q=\dfrac{1}{2}gt^2+v_ot+C_3}$$
初期条件($${t=0, q=q_0}$$)より $${q_0=C_3}$$
よって$${q=\dfrac{1}{2}gt^2+v_ot+q_0}$$ (H1)'''
(H1)'''(H2)""より$${t}$$を消去して$${q}$$と$${p}$$の関係を求める。
$${q=\dfrac{1}{2}gt^2+v_ot+q_0}$$ (H1)'''
$${=\dfrac{g}{2}\Big(t^2+\dfrac{2v_o}{g}t\Big)+q_0=\dfrac{g}{2}\Big\{\Big(t+\dfrac{v_o}{g}\Big)^2-\dfrac{v_0^2}{g^2}\Big\}+q_0}$$
$${=\dfrac{g}{2}\Big(t+\dfrac{v_o}{g}\Big)^2-\dfrac{v_0^2}{2g}+q_0}$$ ← (H2)''を代入
$${=\dfrac{g}{2}\Big(\dfrac{p-mv_0}{mg}+\dfrac{v_o}{g}\Big)^2-\dfrac{v_0^2}{2g}+q_0}$$
$${=\dfrac{g}{2}\Big(\dfrac{p-mv_0+mv_0}{mg}\Big)^2-\dfrac{v_0^2}{2g}+q_0=\dfrac{g}{2}\Big(\dfrac{p}{mg}\Big)^2-\dfrac{v_0^2}{2g}+q_0}$$
$${=\dfrac{p^2}{2m^2g}-\dfrac{v_0^2}{2g}+q_0}$$ (q-p)
または
$${=\dfrac{p^2}{2m^2g}-\dfrac{m^2v_0^2}{2m^2g}+q_0=\dfrac{p^2}{2m^2g}-\dfrac{p_0^2}{2m^2g}+q_0}$$
$${=\dfrac{1}{2m^2g}(p^2-p_0^2)+q_0}$$ (q-p)'
以上よりトラジェクトリーは、$${q}$$軸に頂点をおく$${q}$$軸方向に開いた2次曲線上にあり、起点は$${(q_0, mv_0)}$$である。

初期条件により場合分けを行う。
2-1 自由落下
$${t=0}$$のとき $${q=q_0=0, \dot{q}=v_0=0}$$ $${p_0=mv_0=0}$$
トラジェクトリーは
(q-p)$${q=\dfrac{1}{2m^2g}p^2}$$上、 起点は$${(q_0, p_0)=(0, 0)}$$
(H1)$${\dot{q}=gt>0}$$(時間と共に加速)
(H2)$${\dot{p}=mg>0}$$(速度一定)
よって $${q}$$軸正方向、$${p}$$軸正方向に移動
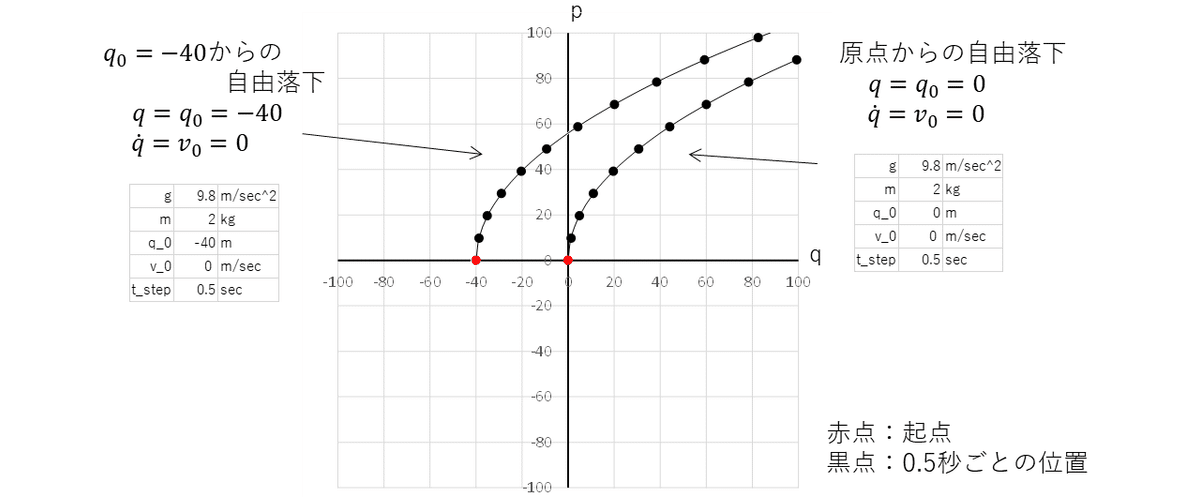
2-2 投げおろし
$${t=0}$$のとき$${q=q_0, \dot{q}=v_0>0, p_0=mv_0>0}$$
トラジェクトリーは
(q-p)$${q=\dfrac{1}{2m^2g}p^2-\dfrac{v_0^2}{2g}+q_0}$$上 起点は$${(0,mv_0)}$$
(H1)$${\dot{q}=0×t+v_0=v_0>0}$$(時間と共に加速)
(H2)$${\dot{p}=mg>0}$$(速度一定)
よって$${q}$$軸正方向、$${p}$$軸正方向に移動

2-3 投げ上げ
$${t=0}$$のとき$${q=q_0, \dot{q}=v_0<0, p_0=mv_0<0}$$
トラジェクトリーは
(q-p)$${q=\dfrac{1}{2m^2g}p^2-\dfrac{v_0^2}{2g}+q_0}$$上 起点$${(0,mv_0)}$$
(H1)$${\dot{q}=gt+v_0}$$
$${t=0}$$のとき
起点$${(0,mv_0)}$$ $${q=0, p=mv_0<0}$$
$${0< t<-\dfrac{v_0}{g}}$$($${gt+v_0<0}$$)のとき
起点$${(0,mv_0)}$$~頂点$${(-\dfrac{v_0^2}{2g}+q_0,0)}$$ $${\dot{q}<0}$$(減速)
$${t=-\dfrac{v_0}{g}}$$($${gt+v_0=0}$$)のとき
頂点$${(-\dfrac{v_0^2}{2g}+q_0,0), \dot{q}=0}$$(加速なし)
$${\because q=\dfrac{1}{2}g\Big(-\dfrac{v_0}{g}\Big)^2+v_0\Big(-\dfrac{v_0}{g}\Big)+q_0=-\dfrac{v_0^2}{2g}+q_0}$$
$${p=mg\Big(-\dfrac{v_0}{g}\Big)+mv_0=0}$$
$${t>-\dfrac{v_0}{g}}$$すなわち$${gt+v_0>0}$$のとき
$${\dot{q}>0}$$(加速)
(H2)$${\dot{p}=mg>0}$$(速度一定)
よって
起点~頂点は$${q}$$軸負の方向に減速、$${p}$$軸正方向に速度一定で移動、
頂点からは$${q}$$軸正の方向に加速、$${p}$$軸正方向に速度一定で移動。

3 単振動
ここでは非保存力の働かないいわゆる単振動と非保存力が働く減衰振動について考える。
3-1 単振動
質量$${m}$$の物体が壁に固定されたばね(ばね定数$${k}$$)と固定されている。重力などの外力は無い。

$${T=\dfrac{1}{2}m\dot{q}^2}$$ $${U=\displaystyle\int_0^qkq dq=k\Big[\dfrac{q^2}{2}\Big]_0^q=\dfrac{1}{2}kq^2}$$
$${\mathscr{L}=T-U=\dfrac{1}{2}m\dot{q}^2-\dfrac{1}{2}kq^2}$$ (L)
$${p=\dfrac{\partial\mathscr{L}}{\partial\dot{q}}=m\dot{q}}$$ よって$${\dot{q}=\dfrac{p}{m}}$$ (q)
$${\mathscr{H}=p\dot{q}-\mathscr{L}=p\dot{q}-\dfrac{1}{2}m\dot{q}^2+\dfrac{1}{2}kq^2=p\Big(\dfrac{p}{m}\Big)-\dfrac{1}{2}m\Big(\dfrac{p}{m}\Big)^2+\dfrac{1}{2}kq^2}$$
$${=\dfrac{p^2}{2m}+\dfrac{1}{2}kq^2}$$ (H)
Lanrange's eqに代入
$${\dfrac{d}{dt}\dfrac{\partial\mathscr{L}}{\partial\dot{q}}=\dfrac{\partial\mathscr{L}}{\partial{q}}, m\ddot{q}=-kq, \ddot{q}=-\dfrac{k}{m}}$$, $${q=A\cos\Big(\sqrt{\dfrac{k}{m}}+\alpha\Big)}$$ (L2)
初期条件$${t=0}$$のとき$${q=q_0, \dot{q}=0}$$を代入
$${q_0=A\cos\alpha, A=\dfrac{q_0}{\cos\alpha}}$$ (L2)'
$${0=-A\sqrt{\dfrac{k}{m}}\sin\alpha}$$ ←(L2)'を代入
$${0=-\dfrac{q_0}{\cos\alpha}\sqrt{\dfrac{k}{m}}\sin\alpha, \tan\alpha=0, \alpha=0}$$ →(L2)'に代入
$${A=\dfrac{q_0}{\cos0}=q_0}$$ よって $${q=q_0\cos\sqrt{\dfrac{k}{m}} t=q_0\cos\omega t}$$ (q)
$${p=m\dot{q}=-mq_0\sqrt{\dfrac{k}{m}}\sin\sqrt{\dfrac{k}{m}} t=-mq_0\omega\sin\omega t}$$ (p)
(q)(p)より$${t}$$を消去
$${\cos\sqrt{\dfrac{k}{m}} t=\dfrac{q}{q_0}}$$(q)' $${\sin\sqrt{\dfrac{k}{m}} t=-\dfrac{p}{q_0\sqrt{mk}}}$$(p)'
$${(q)'^2+(p)'^2=1}$$
$${\dfrac{q^2}{q_0^2}+\dfrac{p^2}{(q_0\sqrt{mk})^2}=1}$$ または$${\dfrac{q^2}{q_0^2}+\dfrac{p^2}{(mq_0\omega)^2}=1}$$ (q-p)
Hamilton's eqは
$${\dot{q}=\dfrac{dq}{dt}=\dfrac{\partial\mathscr{H}}{\partial p}=\dfrac{p}{m}=-q_0\sqrt{\dfrac{k}{m}}\sin\sqrt{\dfrac{k}{m}} t=-q_0\omega\sin\omega t}$$ (H1)
$${\dot{p}=\dfrac{dp}{dt}=-\dfrac{\partial\mathscr{H}}{\partial q}=-kq=ーkq_0\cos\sqrt{\dfrac{k}{m}} t=ーkq_0\cos\omega t}$$ (H2)
トラジェクトリーは
(q-p)$${\dfrac{q^2}{q_0^2}+\dfrac{p^2}{(mq_0\omega)^2}=1}$$
$${q_o, mq_0\omega}$$を各径とする楕円、$${(q_0,0)}$$を起点として時計回りに移動
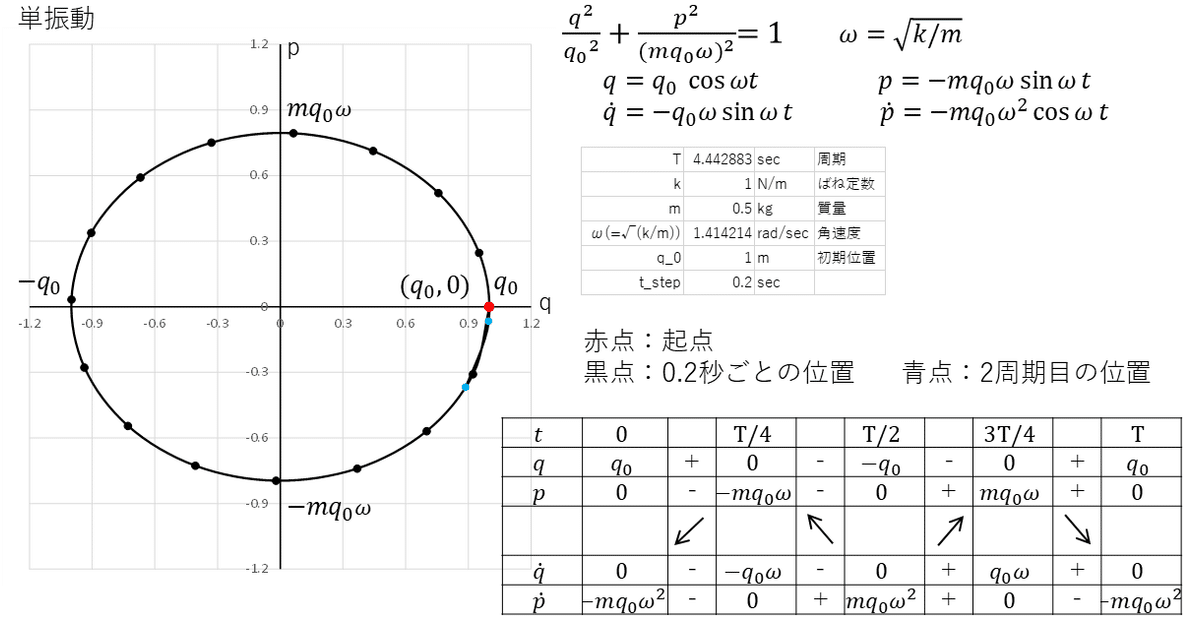
3-2 減衰振動

抵抗力$${b\dot{q}}$$は非保存力なのでLagrangian、Hamiltonianに組み込む方法はここでは選択しない。(→ 散逸関数)
$${m\ddot{q}+b\dot{q}+cq=0}$$のD<0の場合を解くと、減衰振動(5)式より
$${q=q_0\sqrt{\dfrac{4mc}{-D}}\exp\Big(-\dfrac{b}{2m}t\Big)\cos\Big(\dfrac{\sqrt{-D}}{2m}t+B\Big)}$$
ただし $${D=b^2-4mc}$$
$${B=\tan^{-1}\Big(-\dfrac{b}{\sqrt{-D}}\Big)}$$(第4象限とする)
$${\sin(-B)=\dfrac{b}{\sqrt{4mc}}, \cos(-B)=\dfrac{\sqrt{-D}}{\sqrt{4mc}}}$$
$${p=m\dot{q}}$$
$${=mq_0\sqrt{\dfrac{4mc}{-D}}}$$
$${×\Big\{-\dfrac{b}{2m}\exp\Big(-\dfrac{b}{2m}t\Big)\cos\Big(\dfrac{\sqrt{-D}}{2m}t+B\Big)}$$
$${-\dfrac{\sqrt{-D}}{2m}\exp\Big(-\dfrac{b}{2m}t\Big)\sin\Big(\dfrac{\sqrt{-D}}{2m}t+B\Big)\Big\}}$$
$${=-\dfrac{q_0}{2}\sqrt{\dfrac{4mc}{-D}}\exp\Big(-\dfrac{b}{2m}t\Big)}$$
$${×\Big[b\cos\Big(\dfrac{\sqrt{-D}}{2m}t+B\Big)+\sqrt{-D}\sin\Big(\dfrac{\sqrt{-D}}{2m}t+B\Big)\Big\}}$$
$${=-\dfrac{q_0}{2}\sqrt{\dfrac{4mc}{-D}}\exp\Big(-\dfrac{b}{2m}t\Big)\sqrt{b^2+(\sqrt{-D})^2}}$$
$${×\Big\{\dfrac{b}{\sqrt{b^2+(\sqrt{-D})^2}}\cos\Big(\dfrac{\sqrt{-D}}{2m}t+B\Big)}$$
$${+\dfrac{\sqrt{-D}}{\sqrt{b^2+(\sqrt{-D})^2}}\sin\Big(\dfrac{\sqrt{-D}}{2m}t+B\Big)\Big\}}$$
← $${\sqrt{b^2+(\sqrt{-D})^2}=\sqrt{b^2+\{-(b^2-4mc)\}}=\sqrt{4mc}}$$
$${=-\dfrac{q_0}{2}\sqrt{\dfrac{4mc}{-D}}\exp\Big(-\dfrac{b}{2m}t\Big)\sqrt{4mc}}$$
$${×\Big\{\dfrac{b}{\sqrt{4mc}}\cos\Big(\dfrac{\sqrt{-D}}{2m}t+B\Big)+\dfrac{\sqrt{-D}}{\sqrt{4mc}}\sin\Big(\dfrac{\sqrt{-D}}{2m}t+B\Big)\Big\}}$$
← $${\sin(-B)=\dfrac{b}{\sqrt{4mc}}, \cos(-B)=\dfrac{\sqrt{-D}}{\sqrt{4mc}}}$$
$${=-\dfrac{q_0}{2}\dfrac{4mc}{\sqrt{-D}}\exp\Big(-\dfrac{b}{2m}t\Big)}$$
$${×\Big\{\sin(-B)\cos\Big(\dfrac{\sqrt{-D}}{2m}t+B\Big)+\cos(-B)\sin\Big(\dfrac{\sqrt{-D}}{2m}t+B\Big)\Big\}}$$
$${=-q_0\dfrac{2mc}{\sqrt{-D}}\exp\Big(-\dfrac{b}{2m}t\Big)\sin\Big(\dfrac{\sqrt{-D}}{2m}t+B-B\Big)}$$
$${=-q_0\dfrac{2mc}{\sqrt{-D}}\exp\Big(-\dfrac{b}{2m}t\Big)\sin\Big(\dfrac{\sqrt{-D}}{2m}t\Big)}$$
よって
トラジェクトリーは単振動と同様$${(q_0,0)}$$を起点として時計回りに移動しながら原点に向かって収束していき、最終的には運動は停止する。

系に非保存力が働かず保存力のみの下で運動している場合、$${\mathscr{L}=T-U}$$から$${\mathscr{H}=T+U}$$に変換することができる。
このとき$${\mathscr{H}}$$は全力学的エネルギーであり、この式は力学的エネルギー保存の法則を意味する。
※ 保存力とは位置に依存する力である。
その力場には位置エネルギー$${U}$$を導入できるものを指す。
そして、そのなす仕事は経路に依存しない。
$${W=\displaystyle\oint{f dq}=0 , f=-\dfrac{\partial U}{\partial q}}$$
例えば、重力やばねの復元力がそうである。
さて
(H)の$${\mathscr{H}}$$を$${E}$$に置き換えて変形を行うと
(H)$${\mathscr{H}=\dfrac{p^2}{2m}+\dfrac{1}{2}kq^2}$$、 $${E=\dfrac{p^2}{2m}+\dfrac{1}{2}kq^2}$$、 $${1=\dfrac{p^2}{2mE}+\dfrac{kq^2}{2E}}$$
$${\dfrac{p^2}{(\sqrt{2mE})^2}+\dfrac{q^2}{(\sqrt{2E/k})^2}=1}$$ と楕円の式が導かれる。
減衰振動の場合、非保存力$${b\dot{q}}$$によって$${E}$$は
$${\dfrac{dE}{dt}=-b\dot{q}^2}$$の割合で減損していく。( ← 散逸関数(3)式)
よって、楕円の両径は$${E}$$の減損に伴い短くなり、最終的には原点に収束し運動は停止する。
終わりに
1次元座標だけでなく、2次元以上の座標についても書くつもりだったが疲れたので、こんなもんで置いておく。いつか元気なときに追記したい。
