Python で高校数学:複素数平面3題
多角形などの図形を回転したり拡大するのには複素数を使うと便利。
複素数平面(複素平面)は高校の数学Ⅲで学ぶ。したがって,進学校でも文系クラスの生徒は履修しないところが多いだろう。数学Ⅲを学ぶ生徒向けということになるが,まあ,それはそれで。以前の教科書だったら,行列を使うところだ。来年からの新学習指導要領では数学Cの内容となる。
複素数平面と直交座標
まず,複素数平面似ついて,簡単に復習。
直交座標 (x,y) を複素数 x+yi で表すと,平面上の点を複素数で表すことができる。
点zの位置を,原点から見て拡大・縮小するには実数をかける。

複素数の和は平行移動を表す。
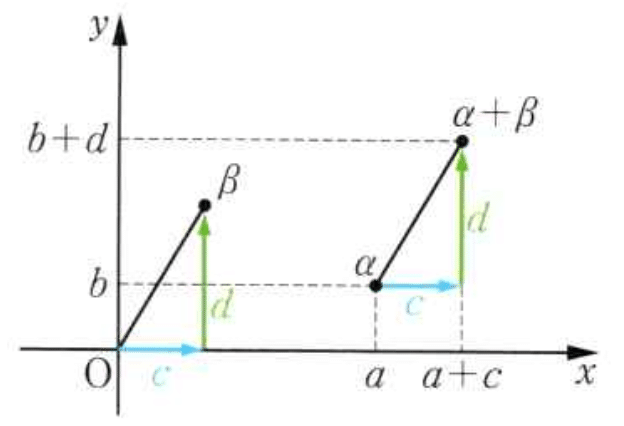
複素数の積は回転と拡大・縮小を表す。
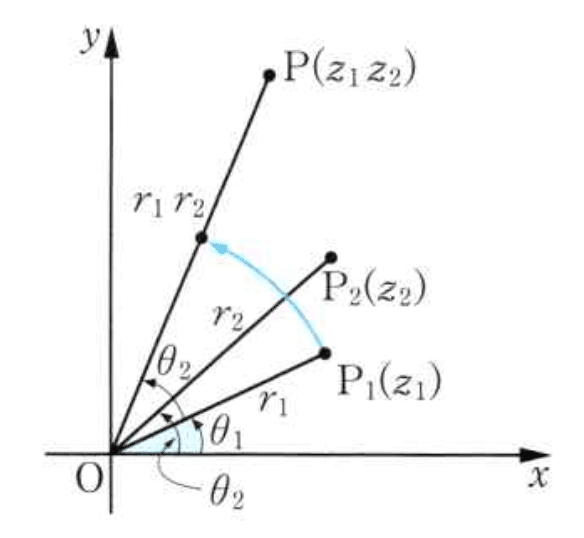
図はいずれも東京書籍の数学Ⅲの教科書から。
x軸とのなす角θを使って,z=r(cosθ+isinθ)と表すことができる。これを極形式という。
直交座標 (x, y)を複素数で表すのに,Pythonでは complex(x,y) を使う。
逆に,複素数 z=x+yiを直交座標にするには,z.real で実部 x ,z.imag で虚部が得られるので [z.real, z.imag] とすればよい。image ではなく imag なので注意。
なお,Pythonでは,虚数単位は i ではなく 1j で表す。これも,1*j ではなく,1j なので注意。数学の教科書にある,たとえば 2+3i だったら,2+3j と表すわけだ。
これを関数化しておくと便利だろう。
# 複素数 z を直交座標 [x,y] に変換
def gauss(z):
return [z.real, z.imag]図を描くための準備
matplotlib.pyplot を使って,折れ線が描けるが,この時,引数は座標のリストではなく,x座標のリストと,対応するy座標のリストだ。これが意外に不便。
そこで,座標のリストを与えて,それらを結んだ折れ線を描く関数を作っておく。
#2点 plist=[p1 ,p2]を結んだ折れ線を描く
def connect(plist, color='b'):
p1 = [p[0] for p in plist]
p2 = [p[1] for p in plist]
plt.plot(p1, p2 , color=color)connect という関数名は,matplotlib に同名の関数があるので,気持ち悪ければ別名にしたほうがいいだろう。
color='b' というのは,キーワード引数で,呼び出すときに指定しなければ青('b')で描くことになる。これも, color=color がちょっと気持ち悪いが,まあいいだろう。このあたり,Pythonの書法に反するかもしれないので,そうであればご指摘願いたい。
また,座標のリストからx座標だけのリスト,y座標だけのリスト使うのに,内包表記を用いている。高校の授業では扱わないほうがいいと思っているので,これらは教員が用意しておくのがよいだろう。このあとの関数もまとめて,モジュールにしてしまえばよい。生徒に書かせるなら for ループで回す。
閉じた多角形は,最初の点と最後の点を結べばよい。引数の plist に plist[0] をappend で追加して connect を呼び出せばよいが,単独で定義するために同じようなことになるが改めて定義しよう。
#点のリスト plist を結んで閉じた多角形を描く
def drawpoly(plist,color='b'):
p1 = [p[0] for p in plist]
p2 = [p[1] for p in plist]
p1.append(p1[0])
p2.append(p2[0])
plt.plot(p1, p2 , color=color)関数名 drawpolyは(connect も)CindyScriptの関数名なので,筆者にはなじみやすいから使っている。もちろん,他の名称でもよい。
単位円に内接する正多角形
単位円周上の点は,x軸とのなす角をθとすると,z=cosθ+isinθ で表すことができる。そこで,単位円周上に内接正角形の頂点をとる関数を次のように作る。ここで,正三角形の頂点が上(y軸上)に来るほうがなんとなく気持ちよいので,90°(π/2)だけずらしている。
#単位円周上に内接正n角形の頂点をとり,そのリストを返す
def apexs(n):
th = 2 * np.pi / n
p = []
for i in range(n):
z = np.cos(np.pi/2 + i*th) + 1j*np.sin(np.pi/2 + i*th)
p.append(gauss(z))
return pこれは生徒に課題として与えてもよさそうだ。gauss(z) は前述のユーザー定義関数。
注意すべきは,i が虚数単位ではなく繰り返しの変数で,虚数単位は 1j であること。生徒が混乱しそうなら,繰り返し変数は別名にしたほうがよいだろう。
それと,円周率は numpy を使っているので np.pi だが,これも np.を忘れそうだ。そこで pai = np.pi として,円周率は pai で表すよ,としておくのも一つの手だろう。
角をθで表すのはキーボード入力が面倒なので th にしている。theta の略だが,これも説明が必要かもしれない。
では使ってみよう。
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.patches as patches
plt.figure(figsize=(4, 4))
ax = plt.axes()
plt.axhline(0)
plt.axvline(0)
# 複素数 z を直交座標 [x,y] に変換
def gauss(z):
return [z.real, z.imag]
#点のリスト plist を結んで閉じた多角形を描く
def drawpoly(plist, color='b'):
p1 = [p[0] for p in plist]
p2 = [p[1] for p in plist]
p1.append(p1[0])
p2.append(p2[0])
plt.plot(p1, p2 , color=color)
#単位円周上に内接正n角形の頂点をとり,そのリストを返す
def apexs(n):
th = 2 * np.pi / n
p = []
for i in range(n):
z = np.cos(np.pi/2 + i*th) + 1j*np.sin(np.pi/2 + i*th)
p.append(gauss(z))
return p
drawpoly(apexs(5))
c1 = patches.Circle([0, 0], 1, fill=False, color='r')
ax.add_patch(c1)
plt.show()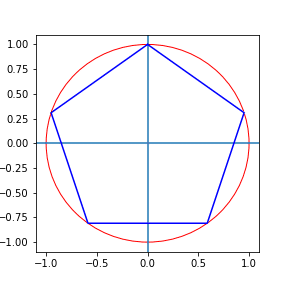
画面設定を最小限のコードにした(自動的に範囲がとられる)が,ひな形が作ってあるのならばそれを使って範囲設定をすればよい。
なお,わざわざ複素数平面にしなくても, sin と cos で円周上の点はとれるわけだが,ここは複素数平面の学習も兼ねている。
正多角形の辺と対角線をすべて描く
単位円周上にとった頂点を2つずつペアにして線分で結ぶ。
まず,ペアを作る関数を作ろう。
# リストのすべての要素の組み合わせからなるリストを返す
def pair(lst):
return [[lst[i], lst[j]] for i in range(len(lst))
for j in range(i+1, len(lst))]内包表記を用いている。長くなるので途中で折り返している。
組み合わせの問題なので,練習問題になりうる。その場合は,内包表記ではなく,for 文のネストで書かせるのがいいだろう。
17角形を作り(円周上に17の点を取り)すべて結ぶと次のようになる。
ap = apexs(17)
appair = pair(ap)
for p in appair:
connect(p)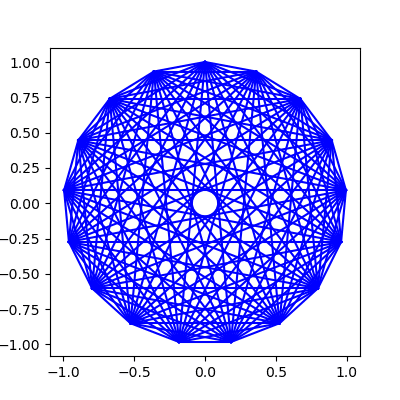
指定した線分を1辺とする正多角形
たとえば,(1,1) と (3,2) を結ぶ線分を1辺として,この上に正多角形を描く。
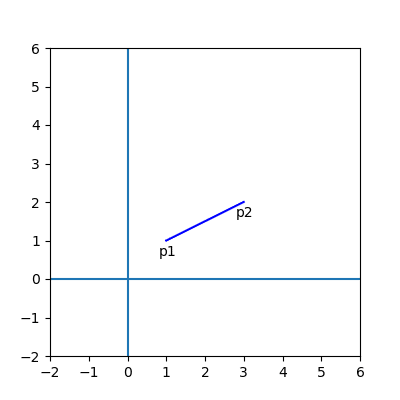
p2 を p1 の周りに回転すればよいのだが,それには,まず全体を p1 が原点にくるように平行移動し,それを回転させてから,ふたたび平行移動して戻す。(図は,東京書籍の教科書)

このとき,多角形の頂点を時計回りにとっていくか,反時計回りにとっていくかの2つの方法がある。上の図で,辺αβからzをとると,反時計回りに作ることになる。βを原点に平行移動して考えると時計回りだ。正方形の場合で示そう。左が反時計回り,右が時計回り。反時計回りにすると,番号の順番がおかしい。
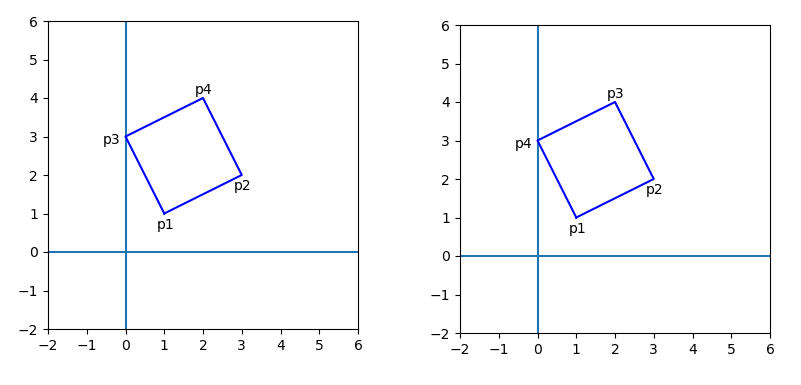
そこで,時計回りに作ることにする。px がx座標のリスト,y座標がy座標のリスト
# p1,p2を結ぶ線分を1辺とする正多角形を時計回りに描く
def regularpoly(p1, p2, n, color='b'):
px = [p1[0], p2[0]]
py = [p1[1], p2[1]]
th = 2 * np.pi / n
z1 = complex(p1[0], p1[1])
z2 = complex(p2[0], p2[1])
for i in range(n-1):
z = z2 + (z2 - z1) * (np.cos(th) + 1j*np.sin(th))
p = gauss(z)
px.append(p[0])
py.append(p[1])
z1 = z2
z2 = z
plt.plot(px, py, color=color)正五角形なら次のように書ける。画面設定は,自動ではなく範囲指定にしている。
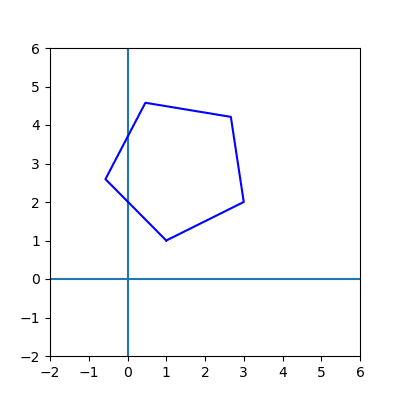
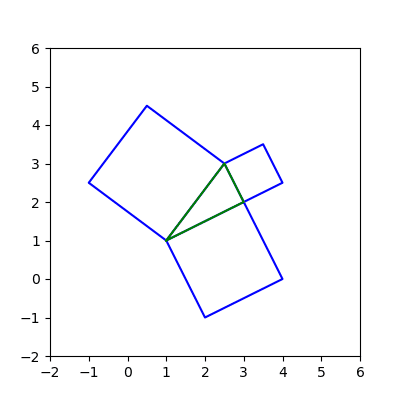
練習問題として,直角三角形をなす3点を指定して,三平方の定理の図を描かせるとよい。
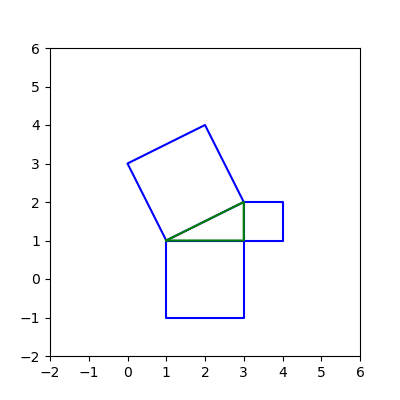
さらに応用課題として,1辺だけを斜めの線で与え,この半分の長さの辺を直角を挟む辺として直角三角形を作ってから,三平方の定理の図にする,というのもあるだろう。