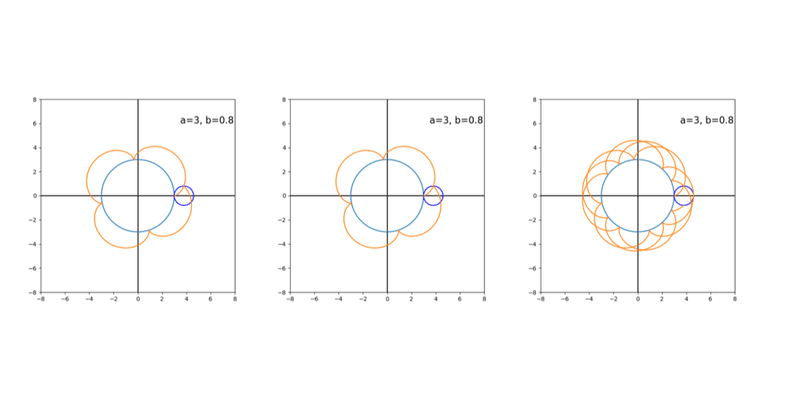
Pythonで高校数学:エピサイクロイド曲線
定円上を外接しながら動円が滑ることなく回転するとき,動円上の定点が描く軌跡がエピサイクロイド曲線である。
サイクロイド曲線ができたので,同様にしてアニメーション版もスライダ版もできる。図形としては定円が一つ増えるだけ。
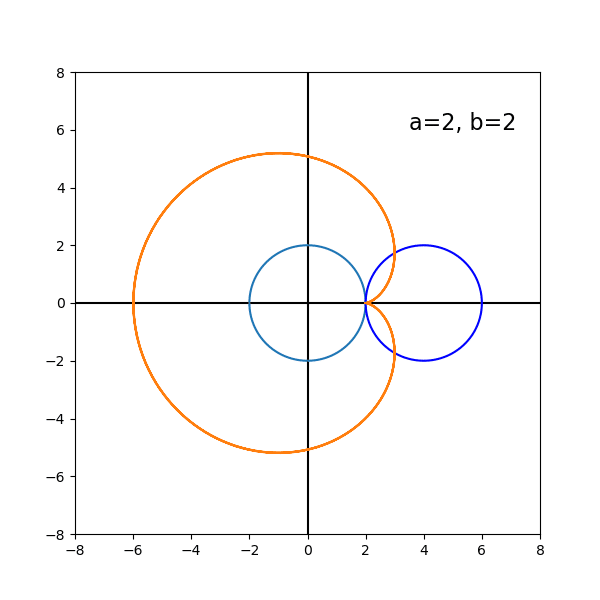
とは言え,定円と動円の半径の比率によっては,なかなか面白い図形が描かれる。半径が等しいときは,カージオイド(心臓形)と呼ばれる。
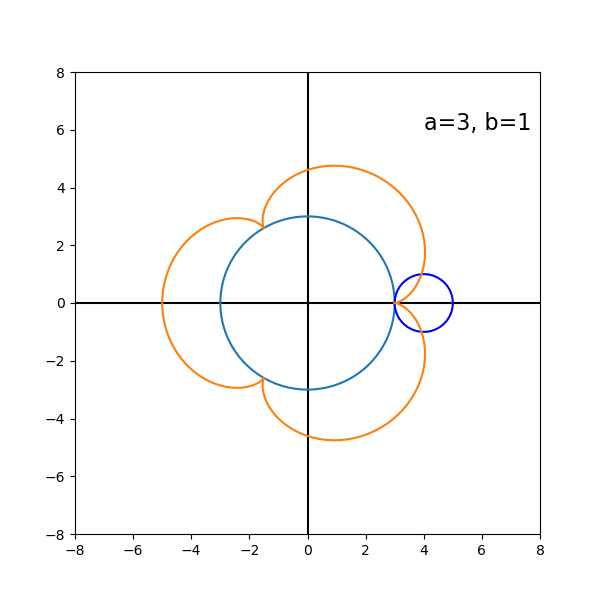
始めは 3:1 くらいがよいかもしれない。
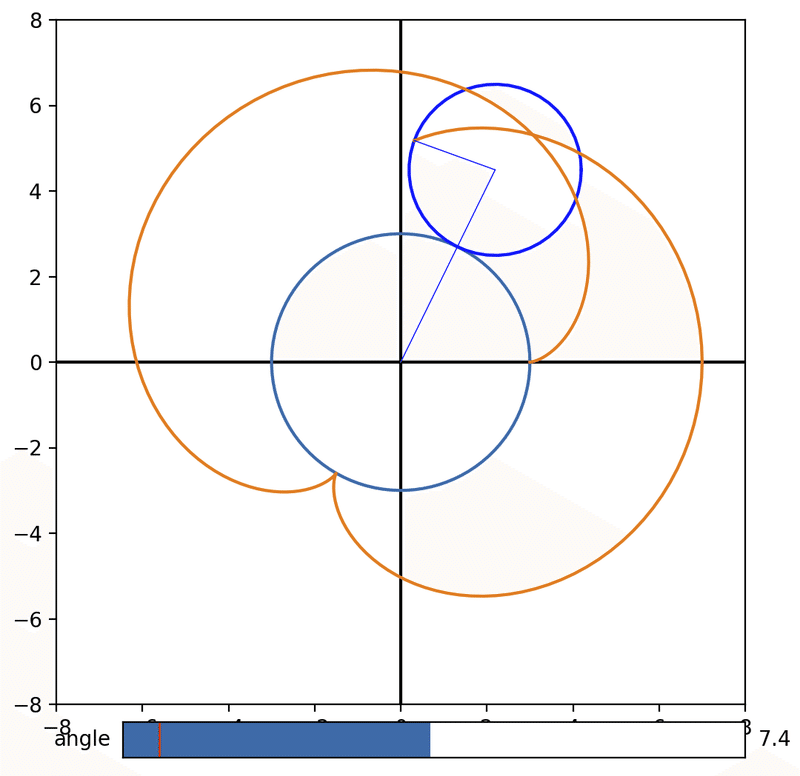
円が一周しただけでは描き終わらないものもある。見出し写真はそんな例。次もそうだ。
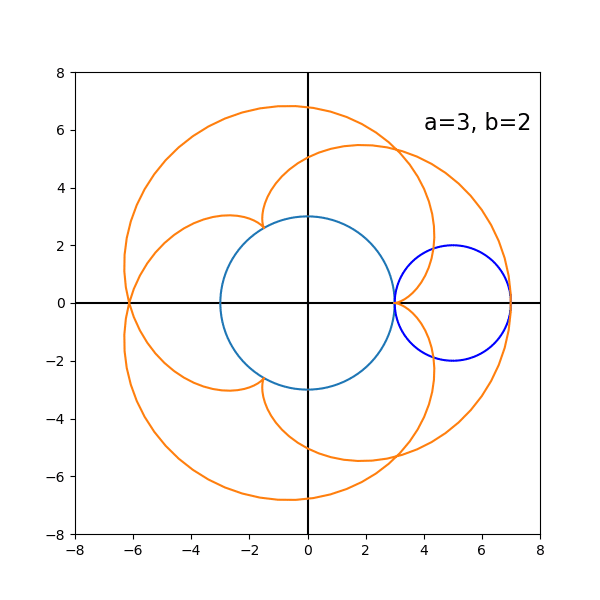
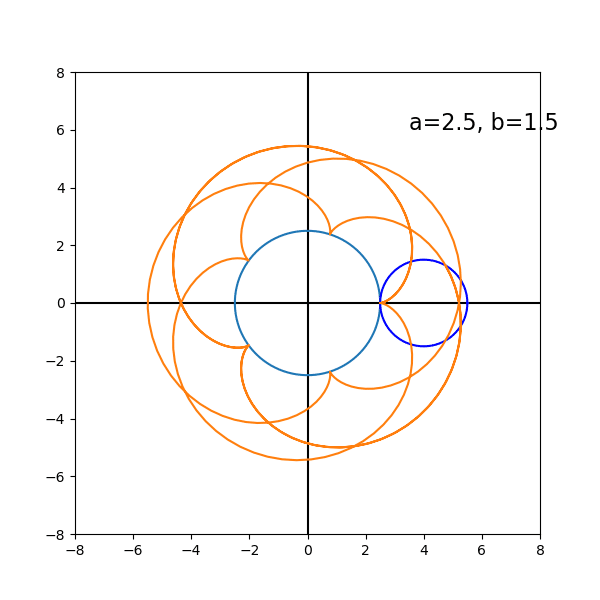
このようにパラメータを変えていろいろ試して興味が出たところで,方程式を求める方法を考えさせ(ただし,ガイドが必要。ヒントなしではまず無理),プログラミングに持っていく。
エピサイクロイドを描く
まずは曲線を描くだけのもの。a,b,stop の3つだけ変更すればよいが,そのあとのコードを読めば曲線の方程式もわかる。
import numpy as np
import matplotlib.pyplot as plt
#定円の半径 a, 動円の半径 b, 周回数 stop
a = 3
b = 0.8
stop = 3
fig = plt.figure(figsize=(6, 6))
ax = plt.axes()
plt.axis([-8, 8, -8, 8])
plt.axhline(0,color='k')
plt.axvline(0,color='k')
# 定円
t = np.linspace(0, 2*np.pi, 100)
x = a * np.cos(t)
y = a * np.sin(t)
plt.plot(x,y)
# 動円
t = np.linspace(0, 2 * np.pi, 100)
x = b * np.cos(t) + a + b
y = b * np.sin(t)
plt.plot(x, y, 'b')
# 曲線
t = np.linspace(0, stop*2*np.pi, 400)
x = (a+b) * np.cos(t) - b*np.cos((a+b)/b*t)
y = (a+b) * np.sin(t) - b*np.sin((a+b)/b*t)
plt.plot(x,y)
plt.text(3.5,6,'a='+str(a)+', b='+str(b), size=16)
plt.show()アニメーション型のエピサイクロイド曲線
作り方の要領はサイクロイド曲線の場合と同じ。
%matplotlib notebook
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.animation as animation
#定円の半径 a 動円の半径 b 周回数 stop 少し手前で止まる
a = 3
b = 1
stop = 1
fig = plt.figure(figsize = (6, 6))
#ax = plt.axes()
# 半径aの定円を描く
def drawcirc():
t = np.linspace(0, 2*np.pi, 100)
x = a * np.cos(t)
y = a * np.sin(t)
plt.plot(x,y)
# エピサイクロイドの媒介変数表示
def epix(t):
return (a+b) * np.cos(t) - b*np.cos((a+b)/b*t)
def epiy(t):
return (a+b) * np.sin(t) - b*np.sin((a+b)/b*t)
def update(frame):
plt.cla()
plt.axis([-8, 8, -8, 8])
plt.axhline(0,color='k')
plt.axvline(0,color='k')
drawcirc()
# 動円を描く
th = frame / 10
cx = (a + b) * np.cos(th)
cy = (a + b) * np.sin(th)
t = np.linspace(0, 2 * np.pi, 50)
x = b * np.cos(t) + cx
y = b * np.sin(t) + cy
plt.plot(x, y, 'b')
t = np.linspace(0, th, 200)
x = epix(t)
y = epiy(t)
plt.plot(x,y)
plt.plot([cx, epix(th)], [cy, epiy(th)],'b', lw=0.5)
plt.plot([0, cx], [0, cy], 'b', lw=0.5)
ani = animation.FuncAnimation(fig, update,
interval=200,
frames=int(np.ceil(63*stop)),
repeat=False)
plt.show()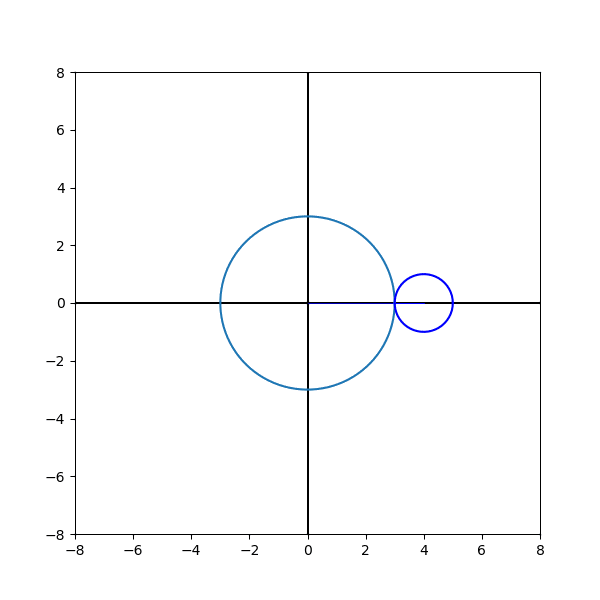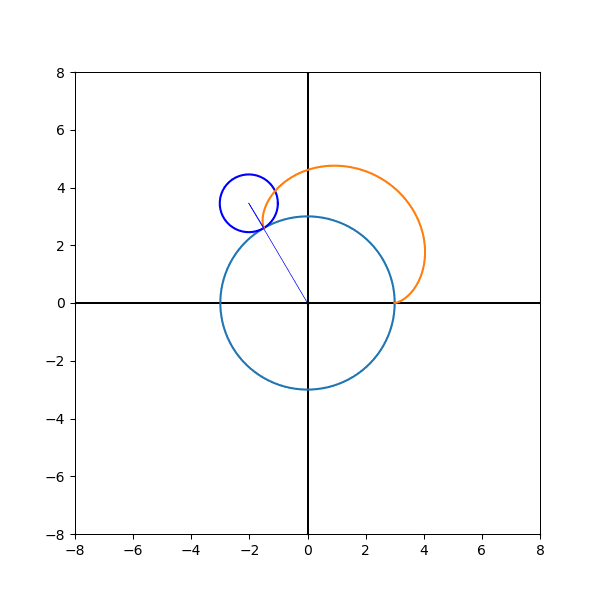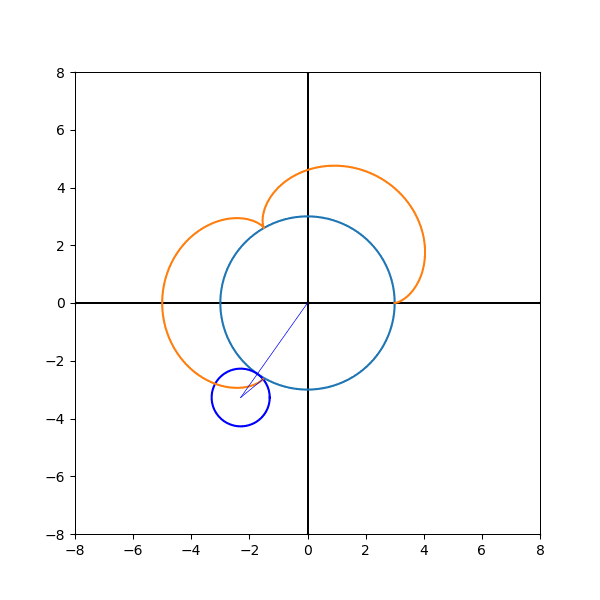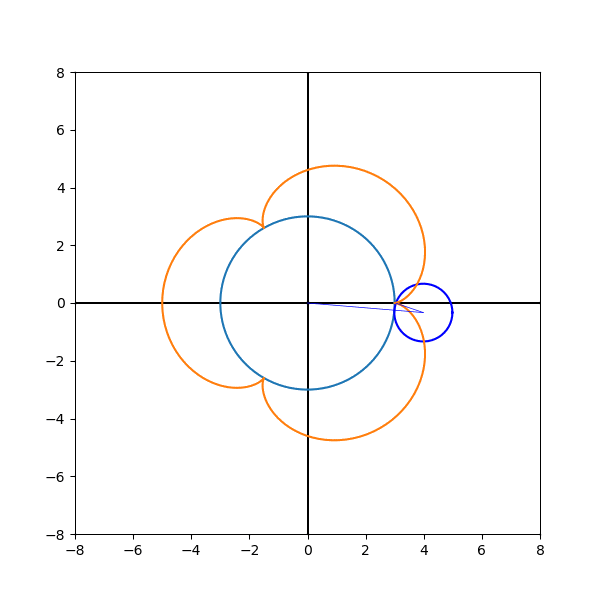
スライダ版エピサイクロイド曲線
%matplotlib notebook
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.widgets as wg
#定円の半径 a 動円の半径 b
a = 2
b = 1
fig = plt.figure(figsize = (6, 6))
ax = plt.axes()
plt.axis([-8, 8, -8, 8])
plt.axhline(0,color='k')
plt.axvline(0,color='k')
# エピサイクロイドの媒介変数表示
def epix(t):
return (a+b) * np.cos(t) - b*np.cos((a+b)/b*t)
def epiy(t):
return (a+b) * np.sin(t) - b*np.sin((a+b)/b*t)
# 半径aの定円
t = np.linspace(0, 2*np.pi, 100)
x = a * np.cos(t)
y = a * np.sin(t)
plt.plot(x,y)
# 動円,軌跡,半径を初期状態で描く
# 軌跡,半径は見かけ上は表示されないがインスタンスを取得
th = 0
cx = (a + b) * np.cos(th)
cy = (a + b) * np.sin(th)
t = np.linspace(0, 2 * np.pi, 50)
x = b * np.cos(t) + cx
y = b * np.sin(t) + cy
g, = plt.plot(x, y, 'b')
t = np.linspace(0, 0, 200)
x = epix(t)
y = epiy(t)
epi, = plt.plot(x,y)
r1, = plt.plot([cx, epix(0)], [cy, epiy(0)],'b', lw=0.5)
r2, = plt.plot([0, cx], [0, cy], 'b', lw=0.5)
# 図を再描画する
def update(th):
cx = (a + b) * np.cos(th)
cy = (a + b) * np.sin(th)
t = np.linspace(0, 2 * np.pi, 50)
x = b * np.cos(t) + cx
y = b * np.sin(t) + cy
g.set_xdata(x)
g.set_ydata(y)
r1.set_xdata([cx, epix(th)])
r1.set_ydata([cy, epiy(th)])
r2.set_xdata([0, cx])
r2.set_ydata([0, cy])
t = np.linspace(0,th, 200)
x = epix(t)
y = epiy(t)
epi.set_xdata(x)
epi.set_ydata(y)
# スライダの位置
sx = plt.axes([0.2, 0.05, 0.7, 0.04])
# スライダの設定
slider = wg.Slider(sx, 'angle',-1, 16, valinit=0, valstep=0.1)
slider.on_changed(update)
plt.show()