Cinderellaでカオスを描く:ジャパニーズアトラクタ
ジャパニーズアトラクタの発見
1961年11月27日、京都大学の大学院生だった上田睆亮(よしすけ)がアナログコンピュータを用いて採取したデータが、後にジャパニーズアトラクタもしくはウエダアトラクタと呼ばれることになるカオスの発見でした。
あのころ私は、たまたま実験中に遭遇したこの神秘的に見える現象に、すっかり平静を失ってしまっていた。自分としては、それは栄光の発見でも何でもなかった。長期間にわたって自分で続けてきたことは、このなんとも落ち着きの悪い現象を頑固に理解しようとし続けてきたことに過ぎない。
と上田睆亮氏は回想しています。その頃の様子は「カオスはこうして発見された」(共立出版)に詳しく書かれています。(かなりドラマティックです)
当時は「カオス」という言葉はありませんでしたし、この発見が「カオスの発見」として認められるのはそれから17年後の1978年のことでした。リュエルが「ジャパニーズアトラクタ」と命名したのです。1961年からためてきたデータは、現在ブルックヘブン研究所に保存されているのですが、その経緯がまた面白い。1986年にヒュー・ブルース・スチュアート博士と会う機会があり、国際会議の1週間の間カオスとの出会いについて話すと、最後の日にスチュアート博士から「ブルックヘブン国立研究所に全資料を保存したい」という申し出を受けます。日本国内では何の価値もないと考え、段ボール2箱の資料を送ります。1988年になってスチュアート博士が来日。ちょっと長いですがその部分を「カオスはこうして発見された」から引用します。
彼は納得がいかないようだった。普段の温かく親しみやすい態度が、徐々に疑い深いものへと変わっていった。私はまるで処刑台に載せられたかのように感じた。それは1988年4月11日のことだった。私はブルックヘブンへ送らなかったいくつかのファイルを取り出し、それを彼に見せた。彼はシワクチャのレポート用紙をつぶさに調べ、走り書きの数値を電卓で検算した。そしてやがて彼は手をたたいて歓声をあげ、納得した表情を見せて、いつものブルースに戻った。私はこれをゴミ捨てによい機会だからと思い、それらのファイルをゴミ箱に放り込んだ。するとブルース氏は「待ってくれ。お願いだからそれも私にくれたまえ」と言った。
ところで、上田がこの現象に遭遇したとき、「最初はアナログコンピュータが故障したのかと思った。しかしすぐに、いやそんなことはないと悟った」と言っていますが、同じようなことをローレンツも言っているのです。
私はすぐに真空管が弱ったか何かの、よくあるコンピュータトラブルを疑ったが、修理を頼む前に、どこで間違いが起ったかだけでも調べてみることにした」(「カオスのエッセンス」共立出版)
これも面白いことです。
ジャパニーズアトラクタを描く
ジャパニーズアトラクタとは、ダフィング方程式の解曲線のアトラクタで、ふつうはそのポアンカレ断面を示します。といっても、なんのことかわかりませんね。すこしずつやっていきましょう。まず、ダフィング方程式です。
ダフィング方程式は、文献によってすこしずつ形が違うのですが、ここでは、上田が大学院生のときに属していた林研究室で研究されていた次の式を扱います。
$${\dfrac{d^2 x}{dt^2}+k \dfrac{dx}{dt}+x^3=B\cos t}$$ ・・・ ①
なお、1961年11月27日にコンピュータが描き出したのは次の式です。
$${\dfrac{d^2 x}{dt^2}-\mu(1-\gamma x^2) \dfrac{dx}{dt}+x^3=B\cos \nu t}$$
こちらは、ファン・デル・ポール/ダフィング混合方程式といいます。
さて、①式は2階の微分方程式です。ここで $${\dfrac{dx}{dt}=y}$$ とおくと、①は次のように1階の連立微分方程式に変形することができます。
$${ \begin{cases}\dfrac{dx}{dy}=y \\ \dfrac{dy}{dt}=-ky-x^3+B \cos t \end{cases}}$$ ・・・ ③
変数が2つになりましたので、xy平面に対応させることができます。このようなものを相空間といいます。また、時間t も含めて3変数と思えば、空間座標系となります。つまり、時間$${t}$$の動きに合わせて、点$${(t,x,y)}$$をプロットしていけば3次元の相空間、$${t}$$を限定して$${(x,y)}$$だけをプロットしていけば2次元の相空間です。③式で、$${t}$$が関わっているのは $${\cos t}$$ です。$${\cos t}$$ は周期2πの周期関数です。そこで、時間$${t}$$を2πずつに区切って点$${(x,y)}$$をプロットしていきます。これが、よく示されているジャパニーズアトラクタです。
③式を差分化しましょう。
$${\begin{cases} x_{n+1}=x_n+(\Delta t)y_n \\ y_{n+1}=y_n+\Delta t(-ky_n-x_n^3+B \cos t) \end{cases}}$$
これを関数として定義しますが、2番目の式は$${t}$$も入っていますので、引数は3つとなります。
時間$${t}$$の刻み幅をどうするかが問題ですが、「理工系シミュレーション入門」に掲載されている、$${\dfrac{2π}{800}}$$ としましょう。
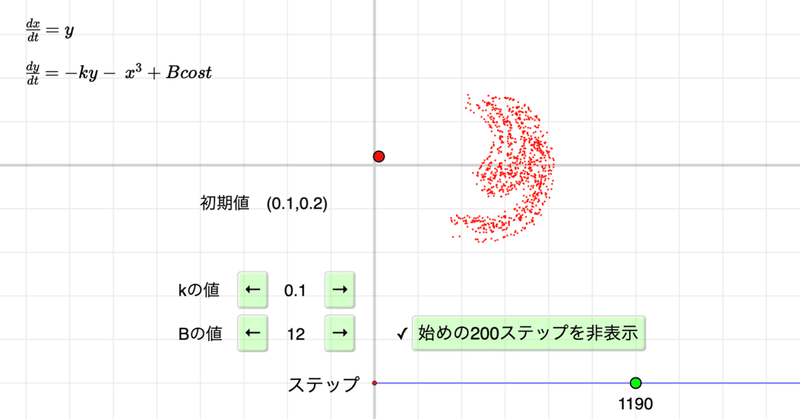
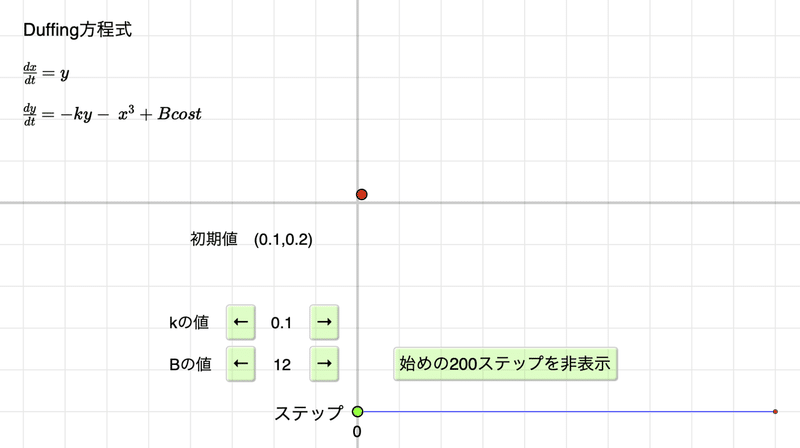
リンク先をひらくと,この条件での図がでます。$${k=0.1,B=12}$$です。
$${k,B}$$ の値と初期値は変えられます。やってみるとわかりますが,アトラクタができるのは,この始めの状態くらいです。数ある値の中で,これを発見したというのも不思議です。
ステップを増やしていくと,始めのうちは次のような図ですが,そのあとにアトラクタが現れてきます。
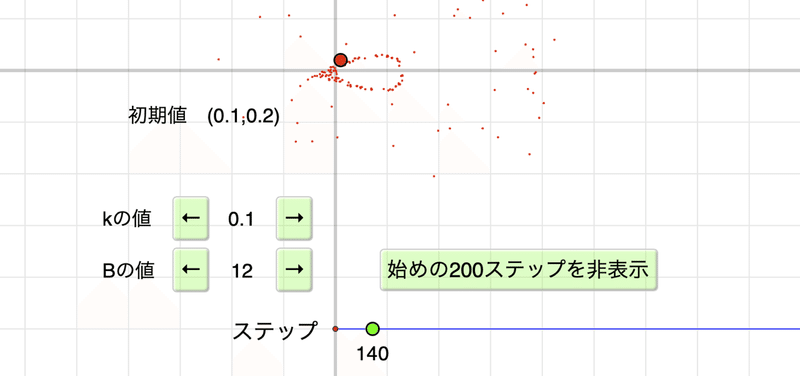
「始めの200ステップを非表示」ボタンを押したのが,見出し画像です。
←前節:グモウスキー・ミラ写像
→次節:池田アトラクタ
