
AIを理解する技術ーSHAPの原理と実装ー
電通デジタルでデータサイエンティストをしている福田です。
これはDentsu Digital Advent Calendar 2021の10日目の記事です。
本記事ではXAIの手法の1つであるSHAPについて解説したいと思います。
XAIとは
XAIとはexplainable AIの略で、説明可能なAIまたはAIの予測結果を説明する技術のことを指します。モデルの解釈性と精度は基本的にはトレードオフの関係にあり、重回帰や決定木のようなわかりやすいモデルがある一方で、精度を求めようとするとXGBoost、LightGBMのような複雑なモデルに頼ることが多いと思います。XAIは後者のような精度は高いが解釈性が低いモデルをターゲットとしています。
SHAP
SHAP(SHapley Additive exPlanation)とは局所的なモデルの説明(1行のデータに対する説明)に該当します。予測値に対して各特徴量がどのくらい寄与しているかを算出する手法で、Shapley値と呼ばれる考え方に基づいています。
Shapley値は元々協力ゲーム理論と呼ばれる分野で提案されたものです。協力ゲーム理論では、複数のプレイヤーが協力してクリアすることで報酬が得られるようなゲームにおいて、各プレイヤーの貢献度に応じて報酬をいかに公平に分配するかを求めることが主なタスクとなっています。機械学習ではいろいろな特徴量が組み合わさって予測値が算出されているので、ゲーム=1行のデータ、プレイヤー=特徴量、報酬=予測値と読み換えることができます。
問題設定としてはそれぞれのプレイヤーの任意の組み合わせでゲームをクリアした際に得られる報酬が定義されており、全員でプレイした際の公平な分配方法を求めるといった感じです。例えばA、B、Cの3人がプレイする場合、プレイヤーの組み合わせとしてはAのみ、Bのみ、Cのみ、AとB、AとC、BとC、AとBとCの全部で7通りが存在し、それぞれの組み合わせにおいてクリアした場合の報酬が異なります。当然ですが、1人だけまたは2人だけでプレイしたときの報酬よりも全員でプレイしたときの報酬の方が大きくなっていることが仮定されています。そうでなければ特定のプレイヤーだけ抜け駆けした方が得になってしまいます。

以上のような問題設定で、各プレイヤーに貢献度に応じた報酬を分配します。Shapley値はこの分配の方法の一つです。例えばプレイヤーCの1人だけでクリアした場合、当然ですがCの貢献が100%なのでCに6の報酬を与えることになるでしょう。他にもAとBの2人でクリアした際の報酬が10、AとBとCの3人でクリアしたときの報酬が17と定められているとすると、この状況においてCは17-10=7の報酬に値する貢献をしたと考えることができます。つまりその人がいるのといないのとで報酬がどれくらい違うかを貢献度と捉えて、全てのパターンについて平均することで各プレイヤーの貢献度=Shapley値を求めることができます。機械学習においても、2つ以上の特徴量が組み合わさることにより予測値が大きく上昇したり下降したりすることがあり、まさにShapley値の考え方が適用できるでしょう。あるプレイヤーがいない・いるの全てのパターンは、1人ずつプレイヤーを加えていく組み合わせを追っていけば求めることができます。

プレイヤーごとに平均を取ることで、Aの貢献度は5.5、Bは4.5、Cは7であると求まります。このようにプレイヤーが増えたことによる報酬の増加を貢献度とすることで、「貢献度の総和=全員が参加した時の報酬」の関係が成り立ち、今の場合も5.5+4.5+7=17となっていることが分かります。この性質を機械学習の場合で考えると、あるデータに対する回帰モデルの予測値が50となっていた場合、特徴量Aが10、特徴量Bが5、特徴量Cが15・・・のように全ての特徴量について和を取ると予測値50と一致するということになります。よって、各特徴量が予測値のうちどのくらい担っているかという、直感的な解釈ができるようになります。(※後述しますが、実際は平均からどれだけリフトさせたかを計算するので、貢献度の総和+平均予測値と予測値が一致します)。このような性質を加法性(additivity)と呼び、Shapley値やSHAPは加法性をはじめとしたいくつかの好ましい性質を持っていることが知られています。
SHAP値の計算の概要
上記の通り、プレイヤー=特徴量、報酬=予測値と捉えることで機械学習においてもShapley値の考え方を利用することができますが、細かいところで多少の違いがあります。
SHAPでは「それぞれの特徴量が予測値にどれだけ影響を及ぼしているか」を、各特徴量が予測値を平均よりどのくらい上昇または下降させたかによって測ります。上述のShapley値では誰もゲームをプレイしなければ報酬は当然ゼロでしたが、SHAPの場合は全ての特徴量がない場合を0ではなく全データに対する予測値の平均値で置き換えることによって、プラス方向の貢献とマイナス方向の貢献の両方が出てくるようになっています。
Shapley値の考え方を機械学習に用いる際に最もハードルとなってくるのが「いくつかの特徴量がない」ときの予測値をいかに求めるかです。KernelSHAPと呼ばれる手法では、「ある」特徴量を固定して「ない」特徴量に関する予測値の平均を取る、いわゆる周辺化が用いられます。実際の機械学習モデルで周辺化をするには、例えば「ない」特徴量を適当に変化させてそのたびに予測値を計算し最後に平均するようなやり方が可能です。ただしこの場合には各特徴量が独立であるという仮定が必要なので、相関が極端に大きな変数が含まれているような場合は注意すべきです。
実装
SHAPを実装してみます。実装はGoogle ColaboratoryでSHAPのバージョンは0.40.0で行いました。対象としたのは分類問題で、アルゴリズムはLightGBMを用いました。ツリー系モデルの場合はTreeSHAPという高速にSHAP値を計算できる手法が提供されており、こちらを使用します。
まずはモデル作成を行います。データはSHAPライブラリに備え付けのAdultデータセットを用いました。このデータセットでは年齢や学歴、家族構成、キャピタルゲインなどのデータから、年収が5万ドルを超えているか否かを予測することがタスクです。
import shap
from sklearn.model_selection import train_test_split
X, y = shap.datasets.adult()
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state = 0)学習の部分は割愛しますが、上記のデータセットに対してLightGBMによる学習を行った結果、テストデータに対するAUCが0.93となりました。このモデルを使って以下のコードでSHAP値を求めることができます。まずTreeExplainerオブジェクトを作成し、shap_valuesメソッドによりSHAP値が得られます。
exp = shap.TreeExplainer(model, feature_perturbation = 'tree_path_dependent', model_output = 'raw')
shap_val = exp.shap_values(X_test)[1]
print(shap_val.shape)
print(shap_val[0])
#出力
(6513, 12)
[-0.16935163 -0.00748791 0.04820449 -0.51493674 -0.22151851 -0.76589019
0.03013875 -0.20383954 -0.23619394 -0.03681011 0.45274736 0.00224594]SHAP値を求めるうえでいくつか注意点があります。まず今回のような2値分類モデルの場合、shap_valuesメソッドの返り値は[ラベル0の予測確率のSHAP値array, ラベル1の予測確率のSHAP値array]のリストになっているため、ラベル1の確率だけを取り出してあげる必要があります。
また、分類問題の場合は引数を特に指定しない限りは、SHAP値の計算はオッズ比に基づいて実行されます。確率値でSHAP値を求めたい場合は、feature_perturbation=’interventional’に変更し、引数dataに学習データを与える必要があります。この辺りはいろいろと制約もあるようなので、詳しくは公式を参照してください。
AdultデータセットにはWork ClassやMarital Statusなどのカテゴリ変数が含まれています。今回のモデリングではLightGBMのcategorical_feature引数を指定して学習を行いましたが、ワンホットエンコーディングの場合はどうすればよいでしょうか?この場合はワンホット化したカラムのSHAP値を全て足し算することで元のカテゴリ変数のSHAP値とすることができます。Shapley値の節で説明しましたが、SHAP値にも加法性があるのでカラム毎のSHAP値を足し算しても同じように予測に対する貢献度として解釈できます。
可視化
SHAPには様々な可視化が用意されており、1つ1つのデータに対するSHAP値はもちろんのこと、それらをまとめることによって大局的な解釈を得ることもできます。
1つのデータに対する可視化はforce_plotメソッドによって行います。
idx = 100
shap.initjs()
shap.force_plot(exp.expected_value[1], shap_val[idx], X_test.iloc[idx])
force plotによってどの変数が予測に効いているのかを視覚的に理解できます。このデータに対しては、Age、Marital Status、Occupation、Relationshipなどが予測値を上昇させる方向に、Capital GainとCapital Lossは下降させる方向に効いていることが分かります。上述の通り、分類モデルなのでforce plotも対数オッズに対して出力されます。
次にsummary plotによって、モデルの大局的な説明を得ることもできます。
shap.summary_plot(shap_val, X_test, plot_type = 'bar')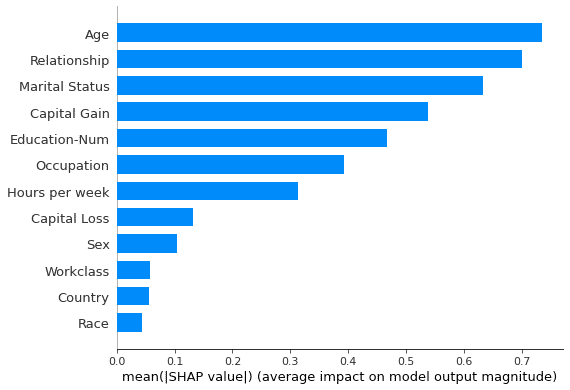
shap.summary_plot(shap_val, X_test)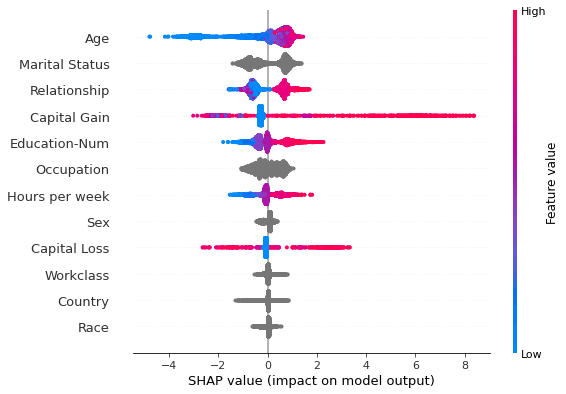
plot_type=’bar’を指定することによって、ツリー系モデルの特徴量重要度と同様のプロットを得ることができます。これは全データに対してSHAP値を求め特徴量ごとに平均した値を表しています。plot_typeを指定しなかった場合、特徴量ごとのSHAP値の分布がプロットされます。色は特徴量の値の高低を表しているので、Ageが低いとSHAP値が小さくなりやすい(=予測に対してマイナスに働きやすい)、高いとSHAP値も大きくなりやすい(予測にプラスに働きやすい)といった大局的な性質が分かります。
dependence_plotにより特徴量の値とSHAP値の関係だけでなく、特徴量同士の交互作用も可視化することができます。
shap.dependence_plot('Age', shap_val, X_test)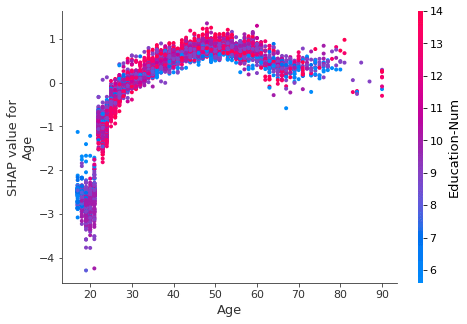
横軸にAge、縦軸にSHAP値を取った散布図が出力されました。Ageが上がるほど予測値にプラスに貢献しやすくなる傾向が分かります。ここまでならばsummary_plotでもある程度読み取れるのですが、カラーバーでEducation-Numの値も表示されているので、Ageが高い人の中でもさらにEducation-Numの値が大きいとよりSHAP値が大きくなりやすいという2変数の交互作用を見て取ることができます。このように同じAgeの値でもSHAP値に分散が生じるのはEducation-Num以外の変数の効果ももちろん含まれていますが、dependence plotでは指定した特徴量と最も交互作用が大きい変数が自動で選択されプロットされるようになっています。
説明の評価
SHAPで得られた説明が本当に正しいかどうかについては、残念ながらデータやモデルから知れる範疇を超えており、ドメイン知識が必要とされます。また、ドメイン知識があったとしても、1つ1つのSHAP値をいちいちチェックしていると膨大な時間がかかってしまいかねません。したがって、summary plotやdependence plot等を活用し大局的な性質を捉え、ドメイン知識と照らし合わせながら、妥当な解釈を得られているかをきちんと精査することが重要でしょう。
まとめ
XAIは様々な場面で必要とされています。中でもSHAPは1つ1つのデータに対する予測根拠を知りたいときに適しています。貸し倒れの予測モデルに対して適用すればなぜその人がローンを借りられないのかを説明することができますし、不適切な予測根拠になっていないかのチェックに使うこともできます。また単純に利用者が納得してAIを使えるようになるので、例えば営業のリード予測モデルなどに対して使用することで、予測値の高い顧客に手当たり次第にアプローチするのではなく、この顧客にはどういったアプローチが効きそうかを担当者が考えるヒントになるかもしれません。AI活用において現場への定着が1つのハードルになる場合も多いと思いますが、今回紹介したSHAPのようなXAI技術によってAIに基づいた意思決定をする上での補足情報を提供することができ、より広く受け入れられるようになることでしょう。
参考文献
[1] XAI(説明可能なAI) その時人工知能はどう考えたのか?, 大坪直樹ほか, リックテレコム
[2] Interpretable Machine Learning, Christoph Molnar
