1. 度数分布とヒストグラム

はじめに

こんにちは、コグラフ株式会社データアナリスト事業部の池田です。
本日から統計学シリーズを書いていきたいと思います！！
BellCurveが運営している統計学webをもとに書いています。 今回は以下の章から学んだことを python で書いています。
基本的に python の説明はしていきませんので分からない箇所は調べていただくかコメントしていただけると嬉しいです。
URLは以下です。
度数分布とヒストグラム

今回は2010年の県の人口分布（ちょっと古い）を使い、作成していこうと思います！
※データを見せる際は小数点を省いていますが、グラフや表では取り除いていません。

用語の紹介

解説をはじめていく前に今から出てくる用語の説明をしていきます！
度数分布表：データをある幅ごとに区切りその中に含まれるデータの度数を
　　　　　　表としてまとめたもの
階級：度数を集計するために区切った区間を表す。
　　　（例：人口が0以上500未満、500以上1000未満）
階級幅：各階級の真ん中の値。
相対度数：各階級の度数が全体に対して占める割合
　　　　　1つの階級の頻度 / 全体の頻度 で求めることができる。
累積相対度数：その階級までの相対度数の累積和。
　　　　　　　その階級までの頻度 / 全体の頻度 で求めることができる。
ヒストグラム：横軸が階級で横軸が頻度のグラフ。
スタージェスの公式：階級の数を算出することができる公式。
ローレンツ曲線：2つの累積相対度数を軸に持つ曲線。
　　　　　　　　各階級の累積相対度数とそれに属する値の累積相対度数。
　　　　　　　　人口データであれば、都道府県とそれに属する人口。
完全平等線：ローレンツ曲線の最初と最後の点を直線で結んだもの。
　　　　　　ローレンツ曲線を描いたときにデータの分布に偏りがない時
　　　　　　それは直線になり y = x となる。
ジニ係数：ローレンツ曲線と完全平等線の差を取り
　　　　　その分布の不均等さを算出したもの。

ヒストグラムの作成

まずはデータを見てみます。

df_2010.head() # 人口データを表示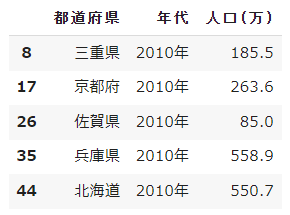

県ごとの人口分布のデータ

python の都合上ヒストグラムの作成が先のほうが楽なので
ヒストグラムの作成最初にしていきます！
まずはスタージェスの公式で階級を決めてそれでグラフを作成してみましょう！

スタージェスの公式

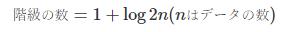
def sturges_formula(data_size):
    return int(round(1+np.log2(data_size),0)) # スタージェスの公式 → 階級幅を決める材料

bins = sturges_formula(len(df_2010))
print("階級数 = ", bins)

階級数 =  7

階級幅を7としてヒストグラムを作成します！
また、matplotlibのヒストグラムでは自動的に階級幅を決めるやり方もあるので、それとの比較もしてみる。

# ヒストグラムの作成
fig = plt.figure(figsize=(10, 5), facecolor="white")

# 階級幅をスタージェスの公式より引用
ax1 = fig.add_subplot(1,2,1) # サブプロットの位置を決定
ax1.set_title("スタージェスの公式で階級幅を決定")
ax1.set_xlabel("人口(万)")
ax1.grid()
n, edge, patches = ax1.hist(df_2010["人口(万)"], rwidth=0.8, orientation='vertical', histtype="stepfilled", range=(0, df_2010["人口(万)"].max()), bins=bins)

# histの引数で階級幅を決定
ax2 = fig.add_subplot(1,2,2)
ax2.set_title("matplotで階級幅を決定")
ax2.set_xlabel("人口(万)")
ax2.grid()
ax2.hist(df_2010["人口(万)"], rwidth=0.8, orientation='vertical', histtype="stepfilled", range=(0, df_2010["人口(万)"].max()))

plt.show()
plt.close()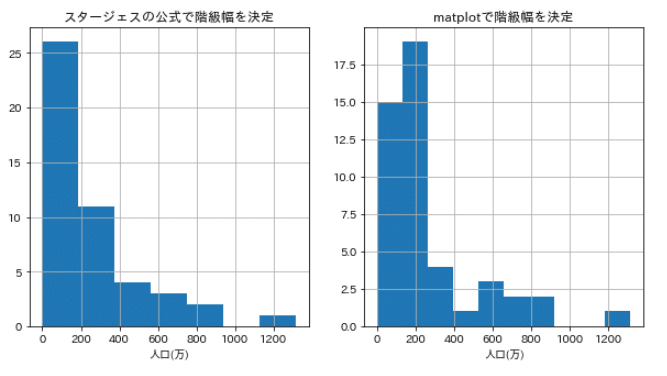

2010年度の都道府県別人口のヒストグラム

スタージェスの公式の階級幅で書いたヒストグラムのほうが階段状になって、視覚的に分かりやすい気がします。細かに見たい場合は matplot での
分布のほうがいいかもしれないですね。今回は前者を使っていきます！
グラフから分かるように人口300万以下の都道府県が
大半を占めていることがわかります。

n, edge, patches = ax1.hist(df_2010["人口(万)"], rwidth=0.8, orientation='vertical', histtype="stepfilled", range=(0, df_2010["人口(万)"].max()), bins=bins)

matplot でヒストグラムを作成したとき、度数と各階級のエッジを返してくれます。それをもとに累積相対度数を追加したグラフを作成してみます。
エッジとは0以上500未満のグラフを書いた場合では0と500がのことです。

print("度数 = ", list(n.astype(int)))
print("階級値 = ", list(np.round(edge)))

度数 =  [26, 11, 4, 3, 2, 0, 1]
階級値 =  [0.0, 188.0, 376.0, 564.0, 752.0, 940.0, 1128.0, 1316.0]

度数を使い累積相対度数を求め、エッジを使い
累計相対度数のグラフ書くために階級値を求めます。（x軸になる）

# 第2軸用値の算出
y2 = np.add.accumulate(n) / n.sum() # accumulateでそれぞれのインデックスの累積値を出している。
rate = n / n.sum() # 相対度数を出す。
x2 = np.convolve(edge, np.ones(2) / 2, mode="same")[1:] # 移動幅を算出している。各階級値の真ん中の値がプロット位置になるように求めている。
print("階級値：", list(np.round(x2)))
print("累積相対度数：", list(np.round(y2,2)))

階級値： [94.0, 282.0, 470.0, 658.0, 846.0, 1034.0, 1222.0]
累積相対度数： [0.55, 0.79, 0.87, 0.94, 0.98, 0.98, 1.0]

求めれました！これを使い先ほどのヒストグラムに
累積相対度数の折れ線グラフを足していきます！

fig = plt.figure(figsize=(10, 5), facecolor="white")
ax1 = fig.add_subplot(1,1,1) # サブプロットの位置を決定
ax1.set_title("2010年の都道府県人口ヒストグラム")
ax1.grid()
n, edge, patches = ax1.hist(df_2010["人口(万)"], rwidth=0.8, orientation='vertical', histtype="stepfilled", range=(0, df_2010["人口(万)"].max()), bins=bins)

# 第2軸のプロット
ax2 = ax1.twinx()
lines = ax2.plot(np.insert(x2, 0, 0), np.insert(y2, 0, 0), ls='--', color='r', marker='s',
         label='累積相対度数') # x軸とy軸に0を入れて視覚的に集中度合いを分かりやすくしている


plt.show()
plt.close()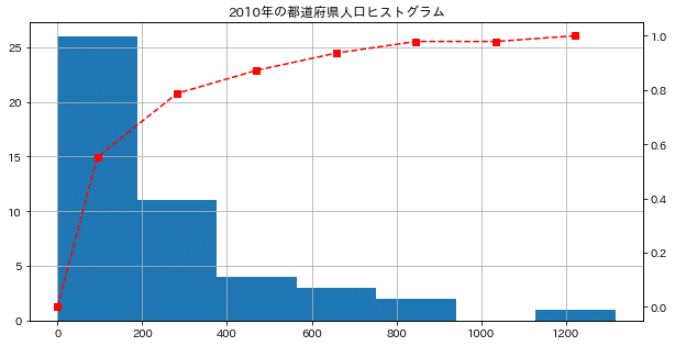

累積相対度数を出すことでどの個所に分布が集中しているか視覚的にとらえやすくなる。 今回だと300万人以下のところに都道府県が集中していて、それ以降はなだらかに推移しているのが直感的に分かる。 またこのような傾いた度数分布を「右裾が長い」などと言う。(逆は「左裾が長い」と言う)

度数分布表

今まで、求めた値を使い度数分布表を作成していきます！

hist_df = pd.DataFrame()
hist_df["階級値"] = x2
hist_df["度数(都道府県)"] = n
hist_df["相対度数(都道府県)"] = rate
hist_df["累積相対度数(都道府県)"] = y2
hist_df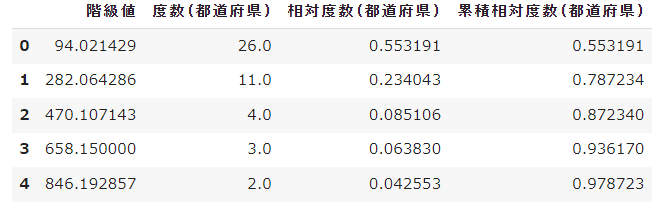

都道府県別人口の分布表

ローレンツ曲線を求めるために、各都道府県に属する
人口の累積相対度数が必要になってきますので、それも求めましょう。

人口の各階級の総数と相対度数と累積相対度数を求めます。
まずは各階級幅で人口の合計値を算出します。

population_lst = []
start = 0
end = 0
for i in range(len(hist_df)):
  start = edge[i]
  if i == len(hist_df) - 1:
    end = edge[i+1] + 1 # 最後は値がかぶっても出せるようにしたい。
  else:
    end = edge[i+1]
  df_2010["population"] = df_2010["人口(万)"]
  population_lst.append(round(df_2010.query("@start <= population < @end").sum()["population"], 2))

population_lst = np.array(population_lst)

それを使い都道府県の累積相対度数をプロットする時に求めたやり方で
相対度数と累積相対度数を算出します。

# 相対度数と累積相対度数を求める。
accum_rate_population = np.add.accumulate(population_lst) / population_lst.sum() # accumulateでそれぞれのインデックスの累積値を出している。
rate_population = population_lst / population_lst.sum() # 相対度数を出す。

print("度数 = ", list(population_lst))
print("相対度数 = ", list(np.round(rate_population,2)))
print("累計相対度数 = ", list(np.round(accum_rate_population,2)))

度数 =  [3081.4, 2541.2, 1993.3, 2082.2, 1791.6, 0.0, 1316.3]
相対度数 =  [0.24, 0.2, 0.16, 0.16, 0.14, 0.0, 0.1]
累計相対度数 =  [0.24, 0.44, 0.59, 0.76, 0.9, 0.9, 1.0]

人口をあわせた度数分布表を作成します。

hist_df["人口(万人)"] = population_lst
hist_df["相対度数(人口)"] = rate_population
hist_df["累積相対度数(人口)"] = accum_rate_population
hist_df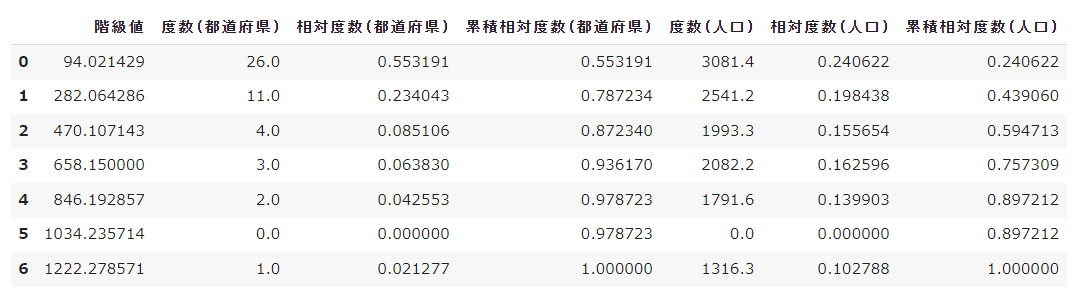

ローレンツ曲線

所得分配の不平等度や人口集中の程度などを
視覚的に捉えるための曲線です。 格差が全くないときは
ローレンツ曲線は完全平等線に沿った直線になり
格差が大きくなるほど完全平等線からの乖離が大きくなります。
ローレンツ曲線を作るためには2つの累積相対度数が必要です。
(例：人口の分布の場合は都道府県の累積相対度数と人口の累積相対度数)

x軸を都道府県の累積相対度数、y軸を人口の累積相対度数とし
プロットしてみましょう！

fig, ax1 = plt.subplots() # サブプロットの位置を決定
ax1.grid()

# 始点を0にする
accum_rate_by_pref = list(hist_df["累積相対度数(都道府県)"])
accum_rate_by_pref.insert(0,0)
accum_rate_by_popu = list(hist_df["累積相対度数(人口)"])
accum_rate_by_popu.insert(0,0)

# ローレンツ曲線のプロット
lines = ax1.plot(accum_rate_by_pref, accum_rate_by_popu, ls='-', color='r', marker='s',
         label='')

# 平等線のプロット
ax2 = ax1.twinx()
lines = ax2.plot([0,1], [0, 1.0], ls='--', color='b', marker='s',
         label='累積相対度数')
ax1.set_xlabel("累積相対度数(都道府県)")
ax1.set_ylabel("累積相対度数(人口)")

plt.show()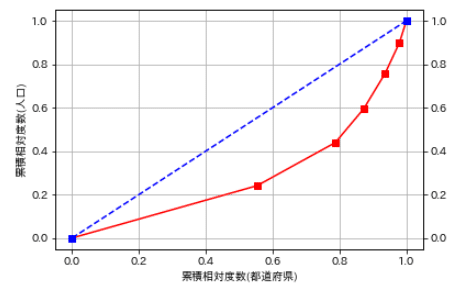

約80%の都道府県内に約50%の人口が集中し残り20%の都道府県内に
もう半分の人口が集中しているのがわかります。
グラフで見て分かるように人口の分布は不均衡であるのが分かります。
ジニ係数を求めてどれほどの偏りがあるか数値化してみます。

ジニ係数

完全平等線と、ローレンツ曲線の間の面積を求めます。
（上記グラフだと青と赤の折れ線グラフの間の面積）
ジニ係数の求め方
以下のスクショから①は三角形の面積、②と③は台形の面積の公式を使い、 最後に完全平等線が斜辺の三角形の面積を求めたものから①、②、③を引きます。

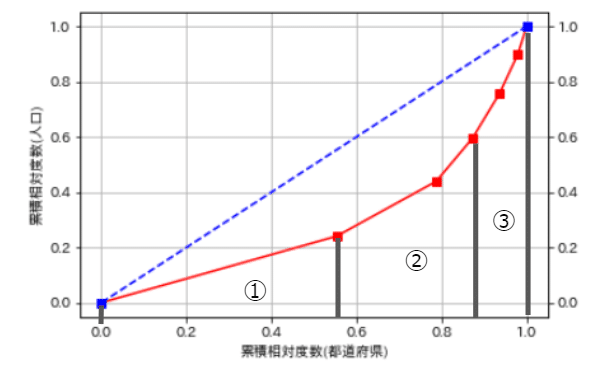
まずは各面積を求めるための値を取得する。（底辺や上底下底）
②と③の分岐は最初の点を除いた1~終点の中央値にする。

# 分布から各面積を求めるための、変数を計算(わかりにくくなるので小数点第二位までにする)

bottom_1 = hist_df["累積相対度数(都道府県)"][0] # ①の底辺
height_1 = hist_df["累積相対度数(人口)"][0] # ①の高さ

initail_p_2 = 1 # ②の開始地点
med_p = round(stats.median(range(1, len(hist_df)))) # ②と③を二つに分割するための中間地点を求める　→　②の最終地点、③の開始地点
final_p_3 = len(hist_df) - 1 # ③の最終地点

top_2 = hist_df["累積相対度数(人口)"][initail_p_2] # ②の上底
bottom_2 = hist_df["累積相対度数(人口)"][med_p]# ②の下底
height_2 = hist_df["累積相対度数(都道府県)"][med_p] - hist_df["累積相対度数(都道府県)"][0] # ②の高さ

top_3 = hist_df["累積相対度数(人口)"][med_p] # ③の上底
bottom_3 = hist_df["累積相対度数(人口)"][final_p_3] # ③の下底
height_3 = hist_df["累積相対度数(都道府県)"][final_p_3] - hist_df["累積相対度数(都道府県)"][med_p] # ③の高さ

print("①の底辺：", round(bottom_1, 2))
print("①の高さ：", round(height_1, 2))

print()
print("中間地点：", (med_p))
print()

print("②の上底：", round(top_2, 2))
print("②の下底：", round(bottom_2, 2))
print("②の高さ：", round(height_2, 2))

print()

print("③の上底：", round(top_3, 2))
print("③の下底：", round(bottom_3, 2))
print("③の高さ：", round(height_3, 2))

①の底辺： 0.55
①の高さ： 0.24

中間地点： 4

②の上底： 0.44
②の下底： 0.9
②の高さ： 0.43

③の上底： 0.9
③の下底： 1.0
③の高さ： 0.02

三角形と台形の公式の関数とジニ係数を求める関数を作成し、
ジニ係数を求める。

# 各公式の関数を作成
def area_of_triangle(bottom, height): # 三角形の面積の公式
  return bottom * height / 2
def area_of_trapezoid(top, bottom, height): # 台形の面積の公式
  return (top + bottom) * height / 2
def calc_gini(triangle_are_1, trapezoid_area_2, trapezoid_area_3): # ジニ係数を求める関数
  equal_line_area = 1 * 1 * (1/2) # いつも一緒
  return (equal_line_area - (triangle_are_1 + trapezoid_area_2 + trapezoid_area_3)) * 2

# それぞれの面積とジニ係数を求める
equal_line_area = 1 * 1 * (1/2) # 完全平等線を斜辺とした三角形の面積
triangle_are_1 = area_of_triangle(bottom_1, height_1) # ①の面積
trapezoid_area_2 = area_of_trapezoid(top_2, bottom_2, height_2) # ②の面積
trapezoid_area_3 = area_of_trapezoid(top_3, bottom_3, height_3) # ③の面積
gini = calc_gini(triangle_are_1, trapezoid_area_2, trapezoid_area_3) # ジニ係数

print("完全平等線の面積：", round(equal_line_area, 2))
print("①の面積：", round(triangle_are_1, 2))
print("②の面積：", round(trapezoid_area_2, 2))
print("③の面積：", round(trapezoid_area_3, 2))
print("ジニ係数：", round(gini, 2))

完全平等線の面積： 0.5
①の面積： 0.07
②の面積： 0.28
③の面積： 0.02
ジニ係数： 0.26

偏りは確かに存在することがわかる。この係数は比較してみないと
大きい小さいが分かりづらいと思いますので、
他の年度の人口分布と比較してみるといいかもしれないですね！
また、より正確にジニ係数を求めるにはローレンツは曲線なので
2点間ごとの面積を求めて合計する必要があります。
ループで正確なジニ係数を求めてみましょう！

areas = 0
prior_height = 0
for i, v in hist_df.iterrows():
  if i == 0: # 三角形の公式を使う
    bottom = v["累積相対度数(都道府県)"]
    height = v["累積相対度数(人口)"]
    prior_height = bottom
    area = area_of_triangle(bottom, height)
  else:
    top = v["累積相対度数(人口)"]
    bottom = v["累積相対度数(人口)"]
    height = v["累積相対度数(都道府県)"] - prior_height
    prior_height = v["累積相対度数(都道府県)"]
    area = area_of_trapezoid(top, bottom, height)

  areas = areas + area

print("ジニ係数：", round((0.5 - areas) * 2, 2)) # ジニ係数

ジニ係数： 0.34

結構差がでましたね。。
python だと簡単に求めれるので、最初から点間の
面積を求めたほうが良さそうですね！

さいごに

以上で、度数分布とヒストグラム編を終了します！
ヒストグラムは業務でも使う場面あると思うので覚えていて
損はないですね。

リンク

Colab：度数分布とヒストグラム.ipynb
次回：さまざまな代表値
　　　平均、中央値、モード、歪度、尖度を求めていきます！！！