
バタフライ効果 - 予測という行為の本質的な難しさについて -
こんにちは。コグラフ株式会社データアナリティクス事業部の塩見です。
自然現象や人間の経済活動では、初期条件のわずかな差が時間経過にしたがって無視できないほどの大きな差が生まれることがあります。この記事では運動方程式をシミュレーションして、磁石に引きよせられる振り子の軌道を描いてお見せします。振り子がまったく予測不可能な動きをする様子をお楽しみください。Pythonを使ってシミュレーションを行っています。Google Colaboratory環境で動きますので、ぜひお試しください。
ブラジルの1匹の蝶の羽ばたきがテキサスで竜巻を引き起こす。こんなことがはたして本当に起こるのでしょうか。
Pythonで微分方程式を解く方法
振り子の運動方程式を解く前に、Pythonで微分方程式を解く方法を簡単なモデルで説明します。
人口のモデル
人口の増加率は現在の人口に比例するモデルを考えましょう。このモデルを微分方程式で表現します。
$$
\frac{dy}{dt}=ky
$$
$${y:}$$ 人口
$${t:}$$ 時間
$${k:}$$ 比例定数
このモデルの解を以下のPythonコードで求めます。比例定数 k = 0.1とし、時間 t = 0から100まで積分します。yの初期値は10にしましょうか。リストで[10]と与えます。
# マルサスの人口モデル
import matplotlib.pyplot as plt
from scipy.integrate import solve_ivp
k = 0.1
def f(t, y): return k * y
sol = solve_ivp(f, [0, 100], [10]) # 時間0から100の範囲で積分する。yの初期値は10。
plt.plot(sol.t, sol.y[0])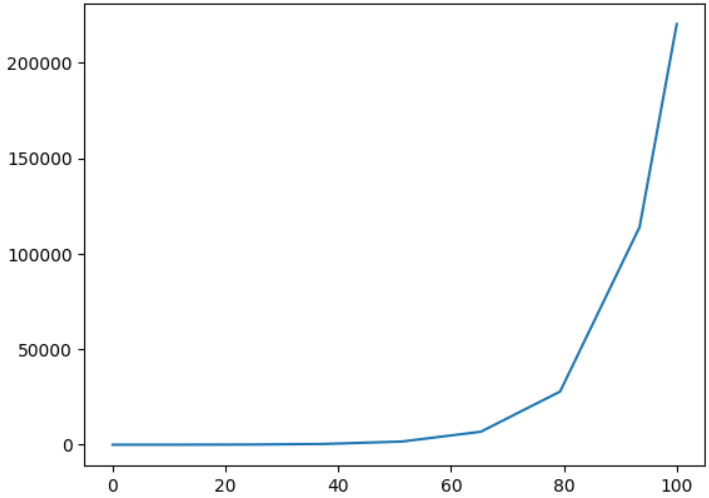
solに格納された結果をプロットするとこのようになります。ガタガタしているのが気になるかもしれませんが、数値計算ライブラリが優れていて、とびとびの値でも精度よく計算できているのでご安心ください。以下のようにt_evalという時間の配列を与えてやればもっとたくさんの点で分割して計算することもできます。
# マルサスの人口モデル(t_eval版)
import numpy as np
import matplotlib.pyplot as plt
from scipy.integrate import solve_ivp
k = 0.1
def f(t, y): return k * y
t_eval = np.linspace(0, 100,100) # 0から100まで100分割した配列
sol = solve_ivp(f, [0, 100], [10], t_eval=t_eval) # 時間0から100の範囲で積分する。yの初期値は10。
plt.plot(sol.t, sol.y[0])
物体の運動モデル
図のようなバネにつながった重りを考えます。

この重りの運動を微分方程式で表現しましょう。
$$
\frac{d^2y}{dt^2}=-ky
$$
$${y:}$$ 重りの変位
$${t:}$$ 時間
$${k:}$$ 比例定数
この式は$${ma=F}$$という運動方程式の形をしていることがわかると思います。二階微分がある運動方程式のようなモデルは、そのままではライブラリで解くことができません。そこで少し変形します。
$$
\begin{cases}
\frac{dy}{dt}=v \\
\frac{dv}{dt}=-ky
\end{cases}
$$
この形式であれば解くことができます。比例定数 k = 1とし、初期値をy = 1, v = 0として、時間0から2πまで積分しました。sol.y[0], sol.y[1]にそれぞれy, vの解が格納されています。
import numpy as np
import matplotlib.pyplot as plt
from scipy.integrate import solve_ivp
# X は [y, v]とする
k = 1
X0 = [1, 0] # 初期値
def f(t, X):
y, v = X # つまり y = X[0], v = X[1]
return [v, -k * y]
t_eval = np.linspace(0, 3.14 * 2, 100)
sol = solve_ivp(f, [0.0, 3.14 * 2], X0, t_eval=t_eval)
plt.plot(sol.y[0], sol.y[1])
磁石に引き寄せられる振り子のモデル
3つの磁石が地面に置かれていて、その上を振り子が揺れている状況を考えます。振り子の重りは鉄でできており、磁石に引き寄せられて、3つの磁石のうちどれかの近くで停止します。磁石の強さは3つとも同じとしましょう。

振り子の運動方程式
ここからは微分を表すドット記法を導入します。ドット一つは時間tでの一階微分、ドット二つは時間tでの二階微分という意味です。振り子の重りが従う運動方程式はこのようになります。
$$
\boldsymbol{\ddot{x}}=\sum_{i}\frac{1}{|\boldsymbol{r_i}|^2}\frac{\boldsymbol{r_i}}{|\boldsymbol{r_i}|}-C\boldsymbol{x}-R\boldsymbol{\dot{x}}
$$
右辺の第一項は磁石による引力、第二項は重りが中心へ戻ろうとする力、第三項は摩擦力や空気抵抗力を表現しています。
$${\boldsymbol{x}}$$は振り子の重りの位置を示すベクトル
$${\boldsymbol{r_i}}$$は重りの位置$${\boldsymbol{x}}$$から$${i}$$番目の磁石の位置$${\boldsymbol{x_i}}$$へのベクトル、つまり
$${\boldsymbol{r_i}=\boldsymbol{x_i}-\boldsymbol{x}}$$
$${|\boldsymbol{r_i}|}$$は$${\boldsymbol{r_i}}$$の大きさ
$${C}$$は重りが中心へ戻る強さ(フックの法則に従う)
$${R}$$は摩擦や空気抵抗の強さ
運動方程式を変形する
ライブラリで計算できるように振り子の運動方程式を変形します。まずは$${\sum}$$の項を単純にします。
$$
\boldsymbol{\ddot{x}}=\sum_{i}\frac{\boldsymbol{r_i}}{|\boldsymbol{r_i}|^3}-C\boldsymbol{x}-R\boldsymbol{\dot{x}}
$$
$${|\boldsymbol{r_i}|^3=|\boldsymbol{r_i}|^{2\cdot (3/2)}=(\boldsymbol{r_i}\cdot\boldsymbol{r_i})^{3/2}}$$と分解することができますので、運動方程式はこのように変形することができます。
$$
\boldsymbol{\ddot{x}}=\sum_{i}\frac{\boldsymbol{r_i}}{(\boldsymbol{r_i}\cdot \boldsymbol{r_i})^{3/2}}-C\boldsymbol{x}-R\boldsymbol{\dot{x}}
$$
本来、このモデルは3次元空間で成り立っているのですが、計算を簡単にするために上空から眺めたような二次元空間で考えたいと思います。ところがそうすると不都合がありまして、重りと磁石の座標が一致すると、$${\boldsymbol{r_i}}$$が$${\boldsymbol{0}}$$となって、0除算が発生して計算できなくなってしまうのです。そこで、分母の計算だけは重りから磁石の位置関係を立体的に考え直し、磁石が設置してある地面から重りまでの高さ$${D}$$を導入します。重りを吊るしている糸は十分に長く、$${D}$$は一定と考えることにして、運動方程式をこのように変更します。
$$
\boldsymbol{\ddot{x}}=\sum_{i}\frac{\boldsymbol{r_i}}{(\boldsymbol{r_i}\cdot \boldsymbol{r_i}+D^2)^{3/2}}-C\boldsymbol{x}-R\boldsymbol{\dot{x}}
$$

ライブラリで計算できるように、二階微分をなくしましょう。
$$
\begin{cases}
\boldsymbol{\dot{x}}=\boldsymbol{v} \\
\boldsymbol{\dot{v}}=\sum_{i}\frac{\boldsymbol{r_i}}{(\boldsymbol{r_i}\cdot \boldsymbol{r_i}+D^2)^{3/2}}-C\boldsymbol{x}-R\boldsymbol{v}
\end{cases}
$$
さらに、ベクトル表記を成分表記に書き換えます。
$$
\boldsymbol{x}=
\begin{bmatrix}
x \
y \
\end{bmatrix}
,
\boldsymbol{v}=
\begin{bmatrix}
u \
v \
\end{bmatrix}
$$
$$
\begin{cases}
\dot{x}=u \\
\dot{y}=v \\
\dot{u}=\sum_{i}\frac{(x_i-x)}{[(x_i-x)^2+(y_i-y)^2+D^2]^{3/2}}-Ru-Cx \\
\dot{v}=\sum_{i}\frac{(y_i-y)}{[(x_i-x)^2+(y_i-y)^2+D^2]^{3/2}}-Rv-Cy
\end{cases}
$$
これで準備完了です。
振り子のシミュレーション
振り子の運動方程式を解いて、重りの軌道を計算してみましょう。以下のPythonコードを実行すると、振り子の重りの軌道を計算して描画します。
import numpy as np
import matplotlib.pyplot as plt
from scipy.integrate import solve_ivp
# 振り子のモデル
def f(t, X):
x, y, u, v = X
u_sum, v_sum = 0, 0
for i in range(3):
tmp_d = ((xi[i] - x)**2 + (yi[i] - y)**2 + D**2)**1.5
u_sum = u_sum + (xi[i] - x) / tmp_d
v_sum = v_sum + (yi[i] - y) / tmp_d
return [u, v, u_sum - R*u - C*x, v_sum - R*v - C*y]
# 磁石を配置
xi = np.array([26, -26, 0])
yi = np.array([-15, -15, 30])
xi = xi / 26
yi = yi / 26
# 物理定数
R = 0.2 # 摩擦や空気抵抗の強さ
C = 0.5 # 重りが中心へ戻る強さ
D = 0.25 # 台から重りへの高さ
MAX_TIME = 100 # 積分する期間の最大値
# 振り子の重りの初期値
x = -1.25
y = -1.8
u = 0
v = 0
X0 = [x, y, u, v]
# 振り子のシミュレーション
t_eval = np.linspace(0, MAX_TIME, 10000)
sol = solve_ivp(f, [0, MAX_TIME], X0, t_eval=t_eval)
# 出力
plt.gca().set_aspect('equal') # 出力の縦横比を同じにする
plt.xlim(-2, 2) # x軸の範囲
plt.ylim(-2, 2) # y軸の範囲
plt.plot(sol.y[0], sol.y[1]) # 重りの軌道をプロット
plt.plot(xi[0], yi[0], marker='.', markersize=20, color="tab:red") # 赤い磁石を表示
plt.plot(xi[1], yi[1], marker='.', markersize=20, color="tab:green") # 緑の磁石を表示
plt.plot(xi[2], yi[2], marker='.', markersize=20, color="tab:blue") # 青い磁石を表示
plt.show();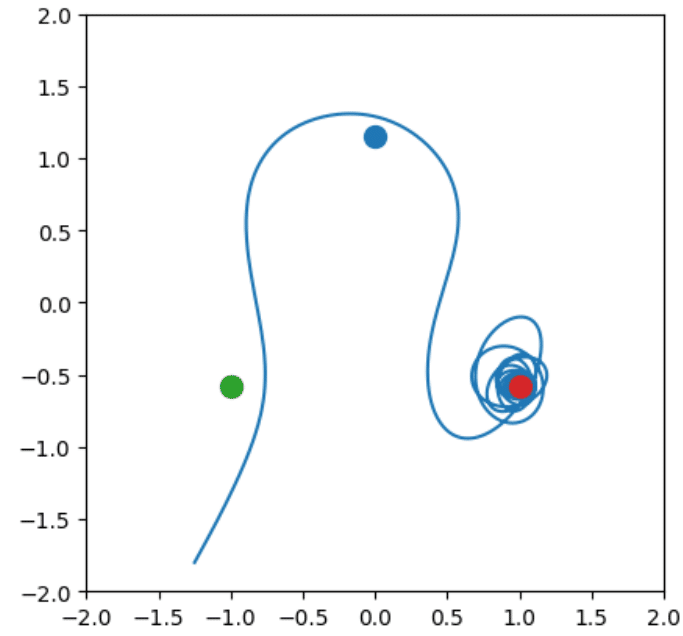
初期値を変えるとまったく異なる結果に
振り子の重りの初期位置を変更すると、たどり着く場所も変わってしまいます。重りの軌道は変化に富んでおり、どの磁石にたどり着くのか事前に予測することはできません。

系の変化が初期条件に極めて鋭敏に依存するため、初期値のわずかな違いがまったく異なる結果をもたらします。このことをもっとわかりやすく可視化してお見せします。どの磁石にたどり着いたかによって、振り子の初期位置を磁石の色で塗り分けました。
import numpy as np
import matplotlib.pyplot as plt
from scipy.integrate import solve_ivp
# 物理定数
R = 0.2 # 摩擦や空気抵抗の強さ
C = 0.5 # 重りが中心へ戻る強さ
D = 0.25 # 台から重りへの高さ
MAX_TIME = 100 # 積分する期間の最大値
# 磁石を配置
xi = np.array([26, -26, 0])
yi = np.array([-15, -15, 30])
xi = xi / 26
yi = yi / 26
# 振り子のモデル
def f(t, X):
x, y, u, v = X
u_sum, v_sum = 0, 0
for i in range(3):
tmp_d = ((xi[i] - x)**2 + (yi[i] - y)**2 + D**2)**1.5
u_sum = u_sum + (xi[i] - x) / tmp_d
v_sum = v_sum + (yi[i] - y) / tmp_d
return [u, v, u_sum - R*u - C*x, v_sum - R*v - C*y]
# 振り子の座標から一番近い磁石を見つける
def find_nearest_magnet(x, y):
distance_list = []
for i in range(3):
distance_list.append((xi[i] - x)**2 + (yi[i] - y)**2)
return np.argmin(distance_list)
pixels = 40 # 画素数を指定
image_rgb = np.zeros((pixels, pixels, 3), dtype = np.uint8) # 色データを保存する配列image_rgbを初期化
u = 0 # 速度の初期値
v = 0 # 速度の初期値
for j in range(pixels):
print(j) # 計算の進捗確認用
for i in range(pixels):
x = (i / (pixels - 1) - 0.5) * 4 # 変数iをx座標に変換
y = (j / (pixels - 1) - 0.5) * 4 # 変数jをy座標に変換
X0 = [x, y, u, v] # 初期値をX0に設定
sol = solve_ivp(f, [0, MAX_TIME], X0) # 振り子のシミュレーション
last_x = sol.y[0][-1] # 重りがたどり着いたx座標
last_y = sol.y[1][-1] # 重りがたどり着いたy座標
magnet_number = find_nearest_magnet(last_x, last_y) # 重りがたどり着いた磁石の番号を求める
# たどり着いた磁石の番号によって配列image_rgbを色分け
if magnet_number == 0:
image_rgb[j][i] = [214, 39, 40] # 赤
elif magnet_number == 1:
image_rgb[j][i] = [44, 160, 44] # 緑
elif magnet_number == 2:
image_rgb[j][i] = [31, 119, 180] # 青
plt.imshow(image_rgb, origin='lower') # 色データ配列image_rgbを表示
plt.show();このコードを実行すると、3分ほどで以下の図が表示されます。磁石の近くでは一番近くの磁石に引き寄せられていますが、少し離れるとまったく予想もつかない磁石にたどり着いていることがわかります。

この記事では「ブラジルの1匹の蝶の羽ばたきがテキサスで竜巻を引き起こす」という言葉で有名なバタフライ効果について、例を示して説明しました。変化の法則が決定論的で、初期条件が決まればその後の状態も一意に決定されるような系であっても、系の変化が初期条件に極めて鋭敏に依存する場合があります。そのような系では、初期条件のわずかな差が時間経過に従って無視できないほどの大きな差を生むことがあるのです。
データ分析に興味のある方募集中!
コグラフ株式会社データアナリティクス事業部ではPythonやSQLの研修を行った後、実務に着手します。
研修内容の充実はもちろん、経験者に相談できる環境が備わっています。
このようにコグラフの研修には、実務を想定し着実にスキルアップを目指す環境があります。
興味がある方は、下記リンクよりお問い合わせください。
X(Twitter)もやってます!
コグラフデータ事業部ではX(Twitter)でも情報を発信しています。
データ分析に興味がある、データアナリストになりたい人など、ぜひフォローお願いします!
📢Wantedly新掲載!
— アラリコ@コグラフ株式会社 | データ事業部 (@CographData) July 14, 2023
「データに興味がある」
「データに携わる仕事がしたい」
そこのあなた!
私たちと一緒にデータ分析しませんか?
IT業界未経験の方も大歓迎です☺️#エンジニア転職 #データ分析 #駆け出しエンジニアと繋がりたいhttps://t.co/S9o7VSjGRt
この記事が気に入ったらサポートをしてみませんか?

