レバレッジものはレンジ相場で目減りする…って？？

てこの原理でスカイハイ！ 
てこは英語でレバー（lever）です。そして、てこの力はレバレッジ（leverage）です。今日はスカイハイ！したい私を含めた多くの潜在的な人々の一助となるべく、レバレッジETFや、レバレッジもの投資信託を算数して (みることを試みて)^n  みます。
※以下「^n」 は累乗を表すものとする。

レバレッジETF（または投信）とは、日々の値動き（価額変動率）が原資産（たとえば株価指数や商品価格）そのものの変動率の一定倍になることを目指して運用しているファンド、と理解してます。
その目論見書を見ると、きまって「レンジ相場では減価していく」旨の注意書きがありますね。レンジ相場とは、上がったり下がったりを繰り返しながらも、おおむね停滞して横ばいの時期。そのとき減価していくって…わかるような、わからないような。
今日はこの点について、算数（というか初等的な数学）を用いて、仮想的なレバレッジ投信を考えたならば、それがどのくらい減価（目減り）していくものなのか、減価割合（の目安）を計算で確かめてみます。

※これは数学的なエントリーであり、具体的商品は一切紹介していません。投資は完全なる自己責任で！！

1. 「パーセンテージのマジック」のこと…ではない！

まず最初にクリアにしておくべき点があります。それはパーセント表示にまつわる落とし穴、今日のお話から除外すべきケースです。

たとえば、原資産となる株価指数がある値（例：1000）だったときに、その日そこから-20％下落して、翌日にまた+20％反発したとすると、結局、値はいくらになっているでしょう？ 1000に戻っているでしょうか？

答えは、

 1000   →(-20％)→   800   →(+20％)→  960 

だから、960ですね。1000には戻りません。

このように、ある日の下落が -r の割合で、翌日の上昇が +r であっても、元の値を 1 としたときには

  1    →    1 × ( 1 - r )    →    1 × ( 1 - r ) × ( 1 + r ) = 1 - r^2

という値になってしまい、-r^2 の分だけ戻りきらないのです。

例
★ r=0.01 （１％）の場合ならば、-r^2 = -0.0001 （-0.01％）
★r=0.04 （4％）の場合なら、-r^2 = -0.0016 （-0.16％）
★r=0.10 （10％）の場合なら、-r^2 = -0.01 （-1％）
★r=0.50 （50％）の場合なら、-r^2 = -0.25 （-25％）
★r=0.xx （xx％）の場合なら、-r^2 = ...

これが「パーセンテージのマジック」、とでも呼ぶべきものです。

しかし、レバレッジものが減価すると言っているのは、これのことではないです。だって上記の話は、レバレッジとは直接関係のない話ですものね？（←原資産も元の値からずれるわけですから）。

2. レバレッジもの特有の減価とは

なので、レバレッジもの特有の減価とは、
「原資産の値が、上下したあとで再びもとの値に（完全に）戻るとき」
に生じているタイプのものと思われます。

仮に株価指数がレンジ相場で1000から800に下落して再び1000に戻ったなら、一日目は-20％、二日目は+25％の変動です。

それに対して、レバレッジ２倍ものは、一日目は-40％、二日目は+50％という値動きになるので、結局どうなるかというと、

1        →    1×(1-0.40)×(1+0.50)
= 1 × 0.6 × 1.5
          = 0.9 （←電卓使用）

と減価しています。これがレバレッジもの特有のシュリンク（減価）の例です（←※原資産や他の１倍投信では発生しない現象だから）。

※これ以外の、レバレッジもの特有の減価の有無はよく知りません。

3. シュリンク率を数式で表す

さて、上記の話を数式（というか文字式）で書くと、いろいろなほかの状況でも計算が容易になって便利です。やりましょう！

★１．
原資産の騰落率が一日目には -r で、二日目には +R となり、結局もとに戻った場合ならば、

 ( 1 - r ) ( 1 + R ) = 1

という関係式が成り立っているはず（←最初に述べたような -r^2 のずれが生じないケースを考えるということ）。
あとで使うためこの式を整理すると、 R に対する次のような条件式が得られます：

R - r = r R  、したがって   R = r / ( 1 - r ) ．

★２．
それに対しレバレッジものの値動きはどうなるか？ レバレッジ倍率を L とすれば、変動率がそれぞれ - L r 、+ L R へと増幅されるから、

 ( 1 - L r ) ( 1 + L R ) = 1 + L ( R - r ) - L^2 r R

となるはず。これを先ほどの条件式を使って書き直せば、

 = 1 + ( L - L^2 ) r R
= 1 + L ( 1 - L ) r R
= 1 - L ( L - 1 ) r R
= 1 - L ( L - 1 ) r^2 / ( 1 - r )

とも書ける ――― つまり L ( L - 1 ) r^2 / ( 1 - r )   という割合の分だけ、評価額がシュリンクするとわかりました：

シュリンク率 =  L ( L - 1 ) r^2 / ( 1 - r ) ．

 L = 1 のときにはこの項が消えることに注意してください。つまり、 L = 1 の原資産では元に戻るが、 L > 1 のレバレッジものだと完全には戻らないというわけです。
（ここまでは、完全に中学数学か高校数学ですよね。）

★３．
というわけで、あとはこの式に好きな数字を入れて電卓等で計算…すればよいですが、暗算でも簡単にシュリンク率の概算ができるように、近似式も求めておきましょう（変動率 r が１よりもそれなりに小さければ成り立つ式を）。
そのためには、等比級数の和の公式（ふつうは高校で習う）により

  1 + r + r^2 + r^3 + r^4 + … = 1 / ( 1 - r )      （ただし r < 1 ）

なる関係が成立していることを使います。すると先ほどの結果は

1 - L ( L - 1 ) r^2 / ( 1 - r ) 
= 1 - L ( L - 1 ) r^2 ( 1 + r + r^2 + … )
= 1 - L ( L - 1 ) ( r^2 + r^3 + r^4 + … )

と書けます。もし r が（ 0.01 や 0.1 など） 1 よりもそれなりに小さい値なら、 r^3 以上の項が r^2 に比べて無視できる（ほど小さくなる）ので、上式は

≒ 1 - L ( L - 1 ) r^2

と近似できます。※誤差はもちろん O( r^3 ) のオーダーです。
したがって、近似的には

 概算シュリンク率 ≒  L ( L - 1 ) r^2 
（１回のみの変動率 r が 1 よりじゅうぶん小さいとき）

という式が成り立つはずだ、との結論が得られました。

※なお、ここまでは -r が下落率(<0)で R が上昇率(>0)としましたが、逆に -r が上昇(>0)で R が下落(<0)のときにも、同じ式が通用することが確かめられます。つまり原資産が下振れするときにも上振れするときにも同じ式でよい。便利！

4. 具体的数値をあてはめ計算してみる

では、最後にお楽しみの時間。いろいろなケースを想定して実際に理論値を概算してみましょう。もちろん、いま求めた推定「公式」を使います：

概算シュリンク率 ≒  L ( L - 1 ) r^2 ，
L : レバレッジ倍率，
r : 原資産の変動率（1周期のみ）

★レバレッジ２倍もの（ L=2 ）のとき
★レバレッジ３倍もの（ L=3 ）のとき
★レバレッジ４倍もの（ L=4 ）のとき
について、表およびグラフを以下に提示します：

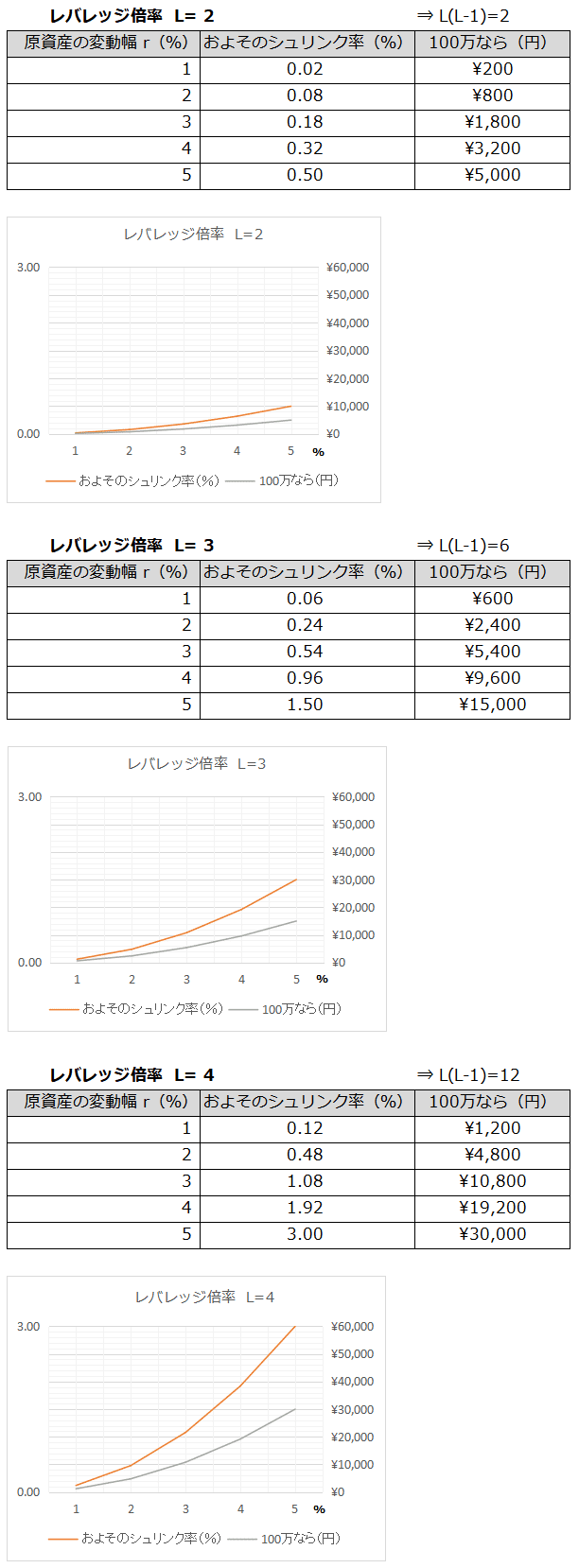
…などなど。

上記は、変動して戻る１回あたりの理論的なシュリンク率ですので、変動が繰り返されれば、同様の割合で何回もシュリンクし続けることになるでしょう。（なので、仮にレバレッジ４倍ものを100万持ってたとして、変動幅３％程度ならば、初回の変動周期でのシュリンクは1万～1.1万円程度、そのあともレンジ相場がしばらく続くとしたら、まぁそこそこいくかもしれません。だから、あとでそれ以上の上ブレを期待したいところではあります。比較のためレバレッジ２倍ものの場合なら、同様のケースでの１回目のシュリンクは2000円前後※1と概算されます。） ※1「1000円前後」から修正しました。

 ＊

いやあそれにしても、減価がどのくらいの率（や額）になるかという感触、計算してはじめてわかりました。
数学って、役に立つなあ…。

さて今日は、「つかみがいつも安易だ」と某先輩に言われたことを２年ぶりくらいに思い出し、迷走の末、テンションを少し上振れさせてしまったかのわさびでした。なーに、これもリスクプレミアムの源泉で、本来歓迎すべきものですよ…

［最後に再び注意： このエントリーは、一般論にもとづき数学的な理想化をほどこした議論で、個人の見解です。内容の正確性にはできるかぎりの注意を払っていますが、正確さを保証するのものではありません。また、具体的商品は一切紹介しておらずそれらの適否も判断しませんので、投資は完全に自己責任でお願いします！］