さるぶつ道場 単振動3解答

半円形レールのついた台と小球の単振動

　問題はこちらです．

　復元力は小球がレールから受ける垂直抗力の水平成分 $${N\sin \theta}$$ です．微小振動なので，$${\theta}$$  が０に近いときに成り立つ近似式 $${\cos \theta\approx 1}$$ を用いて，$${N \cos \theta =mg}$$ より，$${N\approx mg}$$ として運動方程式を立てます．(3)では，小球，及び台にはたらく水平方向の力は，内力である垂直抗力の水平成分のみなので，換算質量を考えると簡単です．(4)は運動量保存則が成り立つので，重心速度が一定である点をイメージしながら解きましょう．(2)，(5)は単振動の速さの最大値は，振幅を半径とする等速円運動の速さの公式 $${v_{Max}=A\omega}$$ を用いると簡単です．

(1)

図1

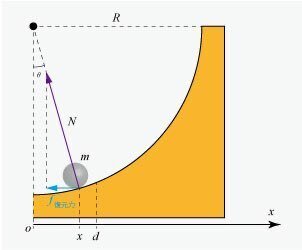
　図1より，小球の位置 $${x}$$ における運動方程式は，小球の加速度を $${a}$$ ，小球が受ける垂直抗力を $${N}$$ として，

$${ma=-N\sin \theta}$$　

 $${R\gg d}$$ より，$${\theta}$$ が０に近いときに成り立つ近似式 $${\cos \theta\approx 1}$$ を用いて，

$${N\approx mg}$$　

　$${\sin \theta =\frac{x}{R}}$$ より，小球の加速度を $${a=-\omega_1^2x}$$ として，

$$
\begin{array}{}
-m\omega_1^2x&=&-\frac{m g}{R}x\\
\omega_1&=&\sqrt{\frac {g}{R}}
\end{array}
$$

　ゆえに，周期 $${T_1}$$ は，

$${T_1=2\pi \sqrt{\frac{R}{ g}}}$$

(2)

　振幅は $${d}$$ なので，

$${v_1=d\omega_1=d\sqrt{\frac{g}{R}}}$$

(3)

図2

　水平方向には大きさ $${N\sin\theta}$$ の内力しかはたらかないので，運動量保存則が成り立つ．

　換算質量 $${\mu}$$ は，

$${\mu =\frac{Mm}{M+m}}$$

　図2のように小球の位置を $${x_1}$$ ，台の位置を $${x_2}$$ ，$${X=x_1-x_2}$$ とすると，$${N\sin\theta}$$ は，

$$
\begin{array}{}
N\sin\theta&=&m g\frac{x_1-x_2}{R}\\
&=&\frac{m g}{R}X
\end{array}
$$

　加速度を $${a=-\omega_2^2X}$$ とすると，運動方程式より，

$$
\begin{array}{}
-\frac{Mm}{M+m}\omega_2^2 X&=&-\frac{m g}{R}X\\
\omega_2&=&\sqrt{\frac{(M+m) g}{MR}}
\end{array}
$$

　ゆえに，周期 $${T_2}$$ は，

$${T_2=2\pi \sqrt{\frac{MR}{(M+m)g}}}$$

(4)

　振動の中心は復元力が0になる点なので，振動の中心 $${x_0}$$ は，

$$
\begin{array}{}
N\sin\theta&=&0\\
mg\frac{x_1-x_2}{R}&=&\\
x_1&=&x_2=x_0
\end{array}
$$

　時間 $${\Delta t}$$ における小球の変位を $${\Delta x_1}$$ ，台の変位を  $${\Delta x_2}$$ とすると，はじめの運動量は0なので，運動量保存則より，

$$
\begin{array}{}
M\frac{\Delta x_2}{\Delta t}+m\frac{\Delta x_1}{\Delta t}&=&0\\
M\Delta x_2+m\Delta x_1&=&0\\
\Delta x_2&=&-\frac{m}{M}\Delta x_1
\end{array}
$$

　したがって，図3より $${x_1=x_2=x_0}$$ となるのは，

図3

$$
\begin{array}{}
x_0&=&-\frac{m}{M}(x_0-d)\\
x_0+\frac{m}{M}x_0&=&\frac{m}{M}d\\
\frac{M+m}{M}x_0&=&\frac{m}{M}d\\
x_0&=&\frac{m}{M+m}d
\end{array}
$$

(5)

　$${x_0}$$ での小球の速さを $${v_b}$$ ，台の速さを $${v_s}$$ とすると，台に対する小球の速さ $${v_2}$$ は，

$$
\begin{array}{}
v_2&=&v_b-(-v_s)\\
&=&\left(d-\frac{m}{M+m}d\right)\omega_2+\frac{m}{M+m}d\omega_2\\
&=&\left(\frac{M}{M+m}+\frac{m}{M+m}\right)d\omega_2\\
&=&d\sqrt{\frac{(M+m) g}{MR}}
\end{array}
$$