さるぶつ道場 運動量保存則6

水平面上での静止している小球との衝突

　なめらかな水平面上に質量 $${m}$$ の小球A，Bがある．図1のように，小球Bを原点に静止させた後，小球Aに $${x}$$ 軸に沿って正方向に大きさ $${p_0}$$ の運動量を与えて小球Bに衝突させた．衝突後，小球Aは $${x}$$ 軸正方向から反時計回りに角 $${\alpha}$$ の向きに，大きさ $${p_A}$$ の運動量で進み，小球Bは $${x}$$ 軸正方向から時計回りに角 $${\beta}$$ の向きに，大きさ $${p_B}$$ の運動量で進んだ．

図1

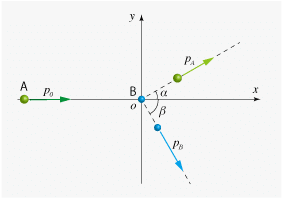
(1) 2つの小球が衝突したとき，小球Aが小球Bから受けた力積を求めよ．
(2) $${p_A}$$ ，及び $${p_B}$$ を $${p_0}$$ ，$${\alpha}$$ ，$${\beta}$$  を用いて表せ．
(3)$${\alpha +\beta=\frac{\pi}{2} }$$ のとき，衝突前後の運動エネルギーの総和の変化量 $${\Delta E}$$ を求めよ．
(4) (3)の結果から，2つの小球の間のはね返り係数 は，次のア～ウのどれか．理由も答えよ．
ア $${e=1}$$　　イ $${1>e>0}$$　　ウ $${e=0}$$

　解答はこちらです．