さるぶつ道場 音4

スピードガンの仕組み

　図1のように，速さ $${v}$$ で $${x}$$ 軸上を等速直線運動する物体Ｐがある．観測者OはＰに振動数 $${f_0}$$ の電磁波を照射して，反射波の振動数を測定することでＰの速さ $${v}$$ を測定する．Ｏから $${x}$$ 軸に下ろした垂線との交点を原点とし，照射する電磁波とＰの進む向きの間の角度を $${\theta}$$ とする．電磁波の速さ $${c}$$ は，Ｐの速さ $${v}$$ に比べて十分に大きく，物体は電磁波を瞬時に反射するものとする．また，電磁波のドップラー効果は，音のドップラー効果と同様に扱ってよいものとする．

図1

(1)Ｐとともに運動する観測者 $${O_P}$$ を考える．$${O_P}$$ が観測する電磁波の波長 $${\lambda _P}$$ を求めよ．
(2) $${O_P}$$ が観測する電磁波の振動数 $${f_P}$$ を求めよ．
(3) Oが観測する反射波の波長 $${\lambda}$$ を求めよ．
(4) Oが観測する反射波の振動数 $${f}$$ を求めよ．
(5) 観測者が発する電磁波の振動数 $${f_0}$$ と，反射波の振動数 $${f}$$ の差 $${\Delta f=f-f_0}$$ を求めよ．ただし，$${c\gg v}$$ なので， $${\frac{v}{c}\ll 1}$$ としてよい．
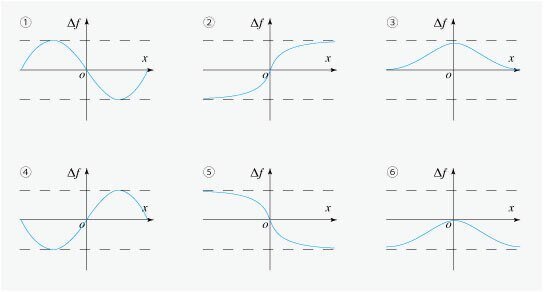
(6) 横軸をPの位置 $${x}$$ ，縦軸を $${\Delta f}$$ としたグラフの概形として，最も適当なものを図2の中から1つ選べ．

図2

　解答はこちらです．