見出し画像

量子コンピューターで機械学習を学ぼう！「QC4U2」に参加してみた-第3回目- 前編

デザイナー │ ヤマモモ

こんにちは、デザイナーのヤマモモです！🙇‍♂️
今日も引き続き、大関さんが量子コンピューターを無料で教えてくれるというオンライン講座の第３回目のレポートを書きます😄

今回は量子機械学習ということで、１回目（量子コンピュータについて）と２回目（機械学習）の講義の合体版という感じになっています。
内容モリモリなんで、今回も前半・後半に分けました😅

↑前回の記事

会員登録してない人でもこの動画視聴できますので、是非御覧ください！


第１回目のおさらい

第１回の序盤でやったようにペニーレイン諸々をインストールしていきます。

アダマール回路を作成

n_qubits = 1
dev = qml.device('lightning.qubit', wires=n_qubits)
@qml.qnode(dev)
def circuitH():
    qml.Hadamard(wires=0)
    return qml.state()

大関さんに言われた通りコピペしました。
これは書き方的には第１回目の時とほぼ同じですね！

H=アダマール

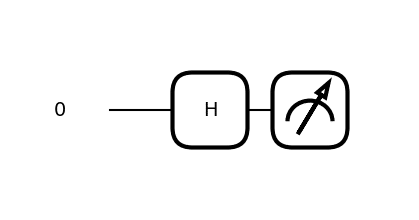
ん？H??
このHというのはHadamard(アダマール)の頭文字です。
第１回目の時はXR（X軸を回転）だったんだけど…どういう状態？🤔

ブロッホ球で表すとこんな感じ

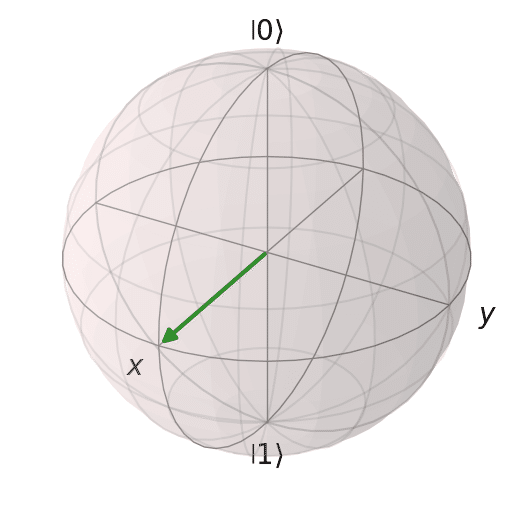
この回路をブロッホ球で表現すると0と1の間で重ね合わせの状態になっているものです。
もっと詳細は大関さんが説明してくれているんですが…（1:06:24）
簡単にH=重ね合わせ状態を作れる！と覚えておくと、この先すごく楽ですｗ 😅

量子状態と確率の関係

ヘイ！アダマール！今の回路の状態は？

じゃあこの重ね合わせの状態は？って聞くと"0.7071〜"って謎の数値が出ます。
なにこれ？🤨

大関さん「この数値を二乗してみて」

確率振幅を二乗すると確率になるよ

0.5と0.5！あ、これ第１回目のときの確率の話しと同じだ！💡
つまり、0が出る確率が50%、1が出る確率が50%ということですね。

じゃあさっきの"0.7071〜"って謎の数字の正体は？
この数字は量子状態の数字が並んだもので、「量子状態ベクトル」と言い、またの名を「確率振幅」と言うそうです。
で、「確率振幅」を二乗すると「確率」になります！

2量子ビットの場合

今までは１量子ビットで回路を作っていました。
次から２量子ビットで作ります！🤯

CZゲートの導入

n_qubits = 2
dev = qml.device('lightning.qubit', wires=n_qubits)
@qml.qnode(dev)
def circuitCZ():
  qml.CZ([0,1])
  return qml.state()

n_qubits = 2
というのが２量子ビット使うという意味だそうです。
新しいCZというのがいる…🫣

CZってこんな感じ

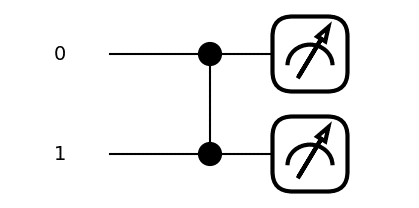
この回路の状態をイラスト化するとこんな感じのものが出て来ました！
０と１がつながっているぞ！
２つの量子ビットが絡む状態で、黒丸で繋ぐのがCZ(コントロールZゲート)というらしいのです。

量子ビットが２つになると色々ルールがあるらしく…😵‍💫

CZの説明

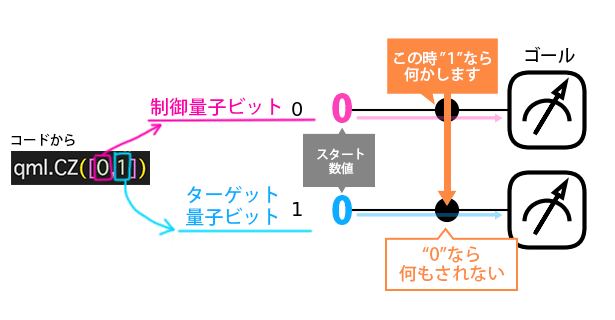
  • 0と1の量子ビットは意味が違って、0を「制御量子ビット」と呼び、１を「ターゲット量子ビット」と呼ぶ

  • 最初は制御量子ビットも、ターゲット量子ビットも0からスタートして右に進んでゴールを目指す

  • 黒●の所で、制御量子ビットが " 1 "だったら(Zゲートを通って)ターゲット量子ビットに何がする(0なら素通り)

混乱しそうなので自分用にメモ

右に進めば進むほど0だった数値が上がるとかはなく「何かしらイベント」がない限り、ただ0のまま進むそうです。
ふーん。じゃあ、最初は両方とも0スタートなら、ゴールは両方とも0じゃない？🤔

この状態でどの確率が出るかを表す確率振幅

じゃあ聞いてみよう！
すげぇ見づらいUI。。（デザイナー的文句☹️w）
左から「00 / 01 / 10 / 11」を表しています。
一番左の00に" 1 "が付いているので、00が100%出るよ！という事です。

ヤマモモの読み正解！！🎉

しかし更にルールは追加される…😇

PauliX

n_qubits = 2
dev = qml.device('lightning.qubit', wires=n_qubits)
@qml.qnode(dev)
def circuitCZ():
  qml.PauliX(0)
  qml.PauliX(1)
  qml.CZ([0,1])
  return qml.state()

大関さんのコピペして。。φ(..)
今度は「PauliX」というのが追加されました😇 (1:42:31)

PauliXを追加した回路の状態

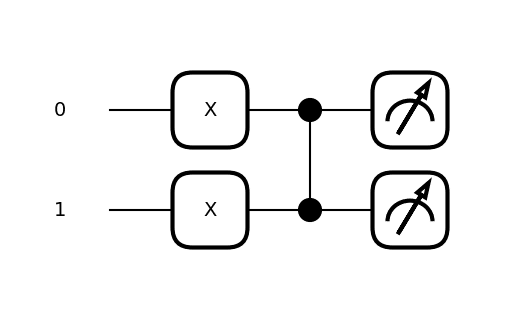
イラストの方にも「X」というものが入りました。
PauliXというのは1を入れたら0に、0を入れたら1に反転するものだそうです。

呪術廻戦？
PauliXを入れた回路の説明図

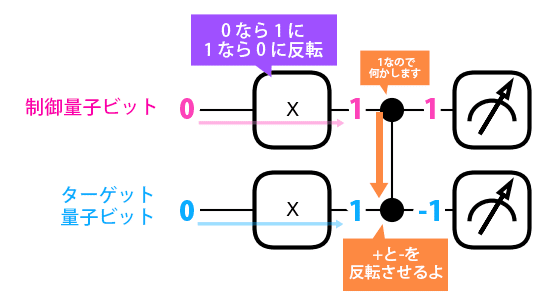
この図だと0からスタートして、Xで両方とも1になる。
制御量子ビットが1だから、黒●の所でZゲートを通って何かされる。
何をされるの？というとターゲット量子ビットの確率振幅の+と-を反転させるんだって🧐
つまり、出てきたのは1と-1でOK？

左から「00 / 01 / 10 / 11」を表しています

右(11)に-1がついている！😎
これは11が100%出るけど、確率振幅の符号が変わって-1となった様子です。
うーん、理解はできたんだけどイマイチ確率振幅が良くわからない…🫠

量子コンピュータは確率的な計算が得意と言われているのですが、でもそれは他のデバイスやシステムでもできますよね？
でも量子コンピュータは確率に関わる数字である確率振幅の＋-、複素数を取ることができるというのも特徴。
確率振幅の二乗が確率なだけであって裏側にある数字はすごい複雑なものを持ってる。(確率というのは0〜100の正の数、だけどそれを示す裏の数字は複素数なのです。)
今は簡単な回路だけど、確率振幅同士で計算させることもできて、さらに別の数値に変化させることもできます。
つまり、確率振幅を操作するのが量子コンピュータの複雑な計算です。

by大関さん
ヤマモモの気持ち

まず複素数って何？😂
複素数のめちゃわかりやすいサイトさん見つけたけど、複素数と確率振幅がどう関係するのかわかりませんでした🥺
うーん、これは数ⅠAしか習ってないヤマモモには難しいわーー＞＜

今までのコンピュータは0を１、1を0に変えるXしか変えられなかった。
でも量子コンピュータでは「Z」というものが増えて、確率振幅の+-を変えられるようになり、自由度が増している。という事でなんとなく理解しました😓

CNOTゲート

n_qubits = 2
dev = qml.device('lightning.qubit', wires=n_qubits)
@qml.qnode(dev)
def circuitCNOT():
  qml.PauliX(0)
  qml.CNOT([0,1])
  return qml.state()

CZではなくCNOTに変わっている😇 (2:20:22)

CNOTゲート回路の状態

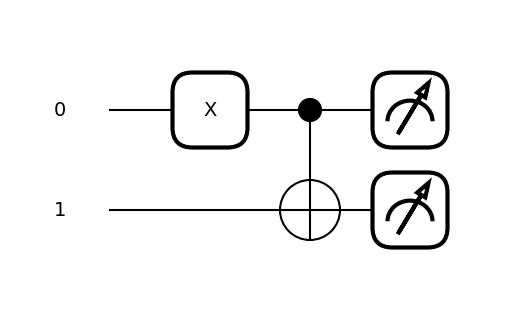
謎の十字丸が増えてますね😓
CNOTゲートは制御量子ビットが１だったら、ターゲット量子ビットが0なら１に。１なら０に反転するそうです。
今までのZゲートとは違い、ターゲット量子ビットが0でも適用されます。

混乱しそうなので自分用にメモ
つまりこういう事？

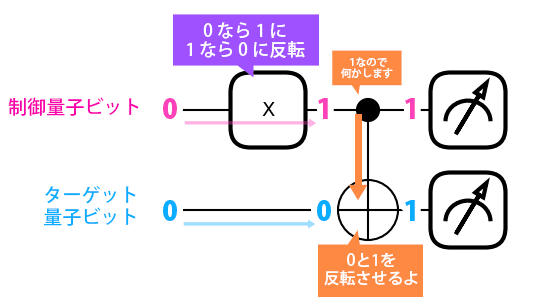
制御量子ビットにXがあるので１になるよね。
黒●で何かされて、ターゲット量子ビットも１になるはず！

左から「00 / 01 / 10 / 11」を表しています

１番右(11)に1がついているんで11が100%出るという事でした！
なんとなくわかってきたけど 複☆雑

一見複雑そうだけど、複雑だぜ

こんな感じでルールが沢山あることがわかりました。
もうこれ以上は覚えられないよ＞＜

重ね合わせの状態×CZゲート=??

大関さん「じゃあ”重ね合わせの状態”４通り（00 / 01 / 10 / 11）を一斉にこの量子回路に入れたら４通り並列計算できちゃうじゃーーーん！」🤩（興奮気味）
確かに、重ね合わせの状態気になる…！😲

n_qubits = 2
dev = qml.device('lightning.qubit', wires=n_qubits)
@qml.qnode(dev)
def circuitH():
  qml.Hadamard(0)
  qml.Hadamard(1)
  qml.CZ([0,1])
  return qml.state()

大関さんのコードをコピペ_φ(･_･
冒頭で出てきた、アダマール（重ね合わせ状態にできるもの）が出てきました。

重ね合わせ状態にしたけど…？

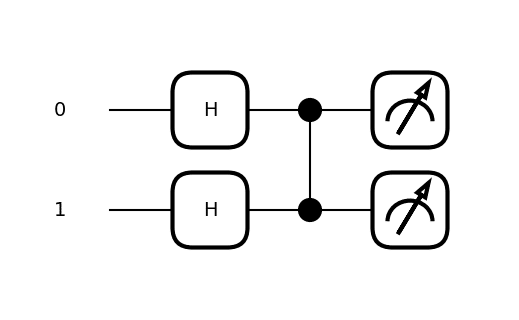
このH(０と１の重ね合わせの状態)を入れたら、どうなってしまうんでしょう？🤔
という事で確率振幅を調べてみます✨

重ね合わせの結果

あれ、全部"0.5"で同じだ😰
これは「四分の一の確率で、どれかが実現するよ」と言っているそうです。
それって全部出る可能性があるよって事だよね？🤔

量子コンピュータで絞り込むということ

絞りこまないと量子コンピュータの並列性は活かせない。
全部重ね合わせて沢山のパターンを出して、ちゃんと絞っていいやつを出すけど、途中で見ちゃだめ。
１つ１つ絞っていって、最終的な結果に落とし込む時「これが出る」という状態にしないと量子コンピュータのご利益は使えません。
そうすれば、何回も測定することなく、確率振幅にゆだねて絞り込んで、数個に絞ってくれる。

by大関さん

これを聞いたとき、私は良くわからなかったんですよね😓
量子コンピュータってデータ打ち込めばいい感じの結果を出してくれるものかと思っていた！と素人的な考えだったのでｗ
だから同僚のM君に聞いてみました(会社に研究者沢山いるんで本当に助かります😊)

M君「量子コンピュータってサイコロを振るのと同じなんですよ。その時に”ある数”が出やすいように細工をするんです。」

えッッッッッッ！？それってイカサマやんけ！！（？）

真っ先に「哲也」が浮かんだヤマモモであった

以下：ヤマモモが中々理解できないので、Mくんが考えてくれた例
例えば100台のトラックがあったとするじゃないですか🚚
その100台に各6ルートずつ与えましょう。

トラック100台のルートを考える

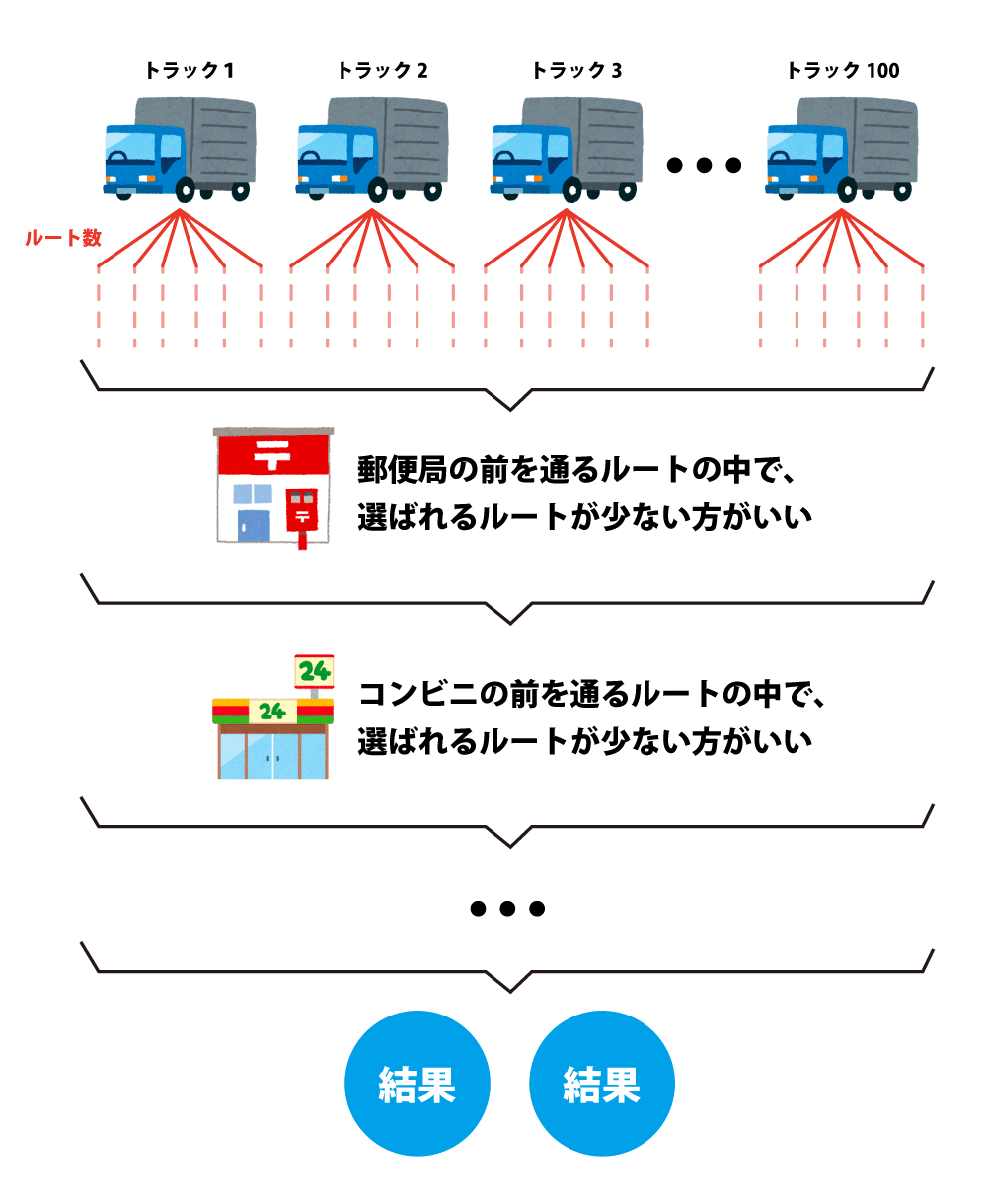
郵便局🏣の前を通るルートばかりだと渋滞しちゃいますよね🚚
　→「郵便局🏣の前を通るルートの中から、選ばれるルートが少ないと良い」
同じように「コンビニ🏪の前を通るルートから〜」「病院🏥の前を通るルートから〜」…etc と人が制約をかけていく事が、細工（＝絞り込む）ということ。
量子コンピュータはこれを最小化するように100個の細工されたサイコロを振ってくれるんすよ🤓

ヤマモモ「あーーーなるほど！それはイメージついたかも！😆」

量子コンピュータは100台×各6ルートの全600パターンどうなるか、実際にトラックを走らせなくても、わかるんですよね。
でも量子コンピュータは、何が最適なのかはわからない。だから人間が制約をつけて絞ってあげることで、最適な答えを出してくれるようになる！
という感じでしょうか💡

前半戦の感想

うーーん、今回も難しかった…色々ルールありすぎる😂
ハンターハンターのアルカのルールよりは理解できたけどｗ
でもこれ、大関さんが教えてくれたのは一部分で、もっと沢山あるんだろうね💦

ハンターハンターのアルカのルール

あと量子コンピュータの基礎的な事が理解できて良かったですｗ
機械学習の時もそうだけど、素人は勝手にいい感じに絞り込んでくれるのかと思った！みたいな思い込みがあるんですよね😅

次回は本格的な量子機械学習に入っていくので、頑張ります！ ﾉｼ

↓次回の記事

この記事が参加している募集

#最近の学び

185,910件

この記事が気に入ったらサポートをしてみませんか？