
宇宙の距離はしご:何億光年も離れた天体までの距離はどのように測られているのか
夜空を彩る無数の天体たちはさまざまな距離に位置していることが知られています.たとえば地球の衛星である月までの距離は約38万キロメートルで,地球が公転している太陽までの距離は約1億5000万キロメートルです.

太陽系の外に目を向けると,最も近い恒星であるアルファ・ケンタウリまでは約4.4光年,隣の銀河であるアンドロメダ銀河までは約250万光年もの距離があります.さらに人類は大型望遠鏡を駆使することで,最近では130億光年以上という途方もなく離れた天体も数多く発見してきています.

では,そういった天体までの距離はどのように測定されているのでしょうか.実は天文学者たちは「宇宙の距離はしご」と呼ばれる方法でこれまでさまざまな距離にある天体までの距離を明らかにしてきました.ごく近くにある天体までの距離を測定するための「はしご」から始まって,より遠くの天体までの距離を測定するための「はしご」へと乗り換えていくイメージです.今回は天体の距離測定法の総称である宇宙の距離はしごについて紹介していきます.
レーザー
月や火星といった地球にきわめて近い天体までの距離は,レーザーを照射して求めることができます.地球から照射したレーザーが光の速さで天体まで届き,反射して地球に返ってくるまでの時間から距離を測定する,という方法です.光の速さはわかっていますから,そこに所要時間をかけることで,光が伝達した距離が得られるというわけです.

月までの距離を正確に測定するため,アメリカのアポロ計画によって月面にはレーザーの反射鏡が設置されました.これによりセンチメートル程度のきわめて高い精度で月までの距離を求められるようになり,月は地球から1年あたり平均3.8センチメートルずつ遠ざかっていることが明らかになりました.

ケプラーの第三法則
レーザーの反射を利用した方法では太陽までの距離を求めることはできません.太陽は明るすぎるためです.太陽までの距離は,他の惑星に対するレーザー反射光による結果とケプラーの第三法則を組み合わせることで求めることができます.ケプラーの第三法則は,「惑星の公転周期の2乗は,惑星の公転軌道の軌道長半径の3乗に比例する」というものです.

たとえば,地球と金星までの距離がわかっていて,地球と金星の公転周期もわかっているとします.このとき,ケプラーの第三法則を用いれば地球と太陽の間の距離を求めることができます.太陽と地球の間の距離を$${a_1}$$,太陽と金星の間の距離を$${a_2}$$とおきます.また,地球の公転周期を$${T_1}$$,金星の公転周期を$${T_2}$$とします.
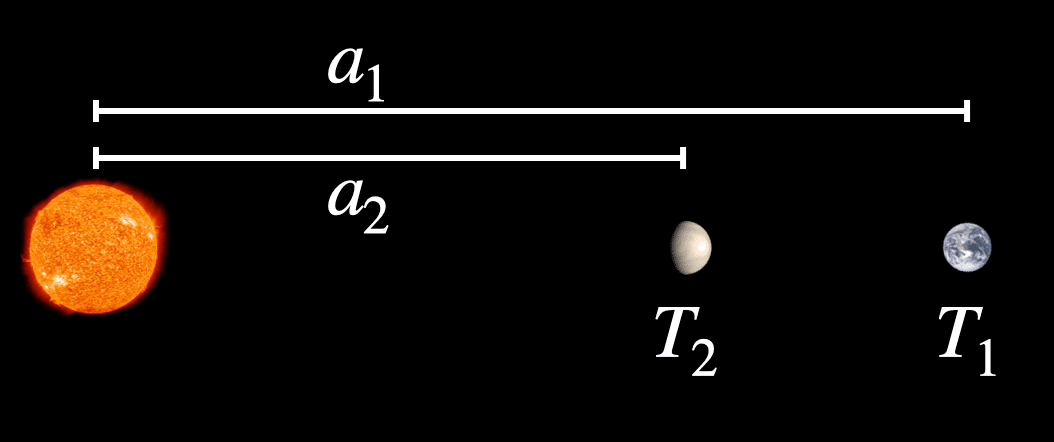
このとき,ケプラーの法則をもとにすると$${a_1}$$をそれ以外の値で表すことができます.
$$
\begin{align*}
T_1^2 \propto a_1^3, \,\,\, T_2^2 \propto a_2^3 \,\,\,
&\to \,\,\, \left( \frac{T_1}{T_2} \right)^2 = \left( \frac{a_1}{a_2} \right)^3 \\
&\to \,\,\, a_1 = a_2 \left( \frac{T_1}{T_2} \right)^{2/3}
\end{align*}
$$
ここで,すでにわかっている地球と金星までの距離を$${L}$$とおくと$${L = a_1 - a_2}$$ですから,これを$${a_2}$$について解くと$${a_2 = a_1 - L}$$です.したがって以下のようになりますから,これを$${a_1}$$について解くとたしかに太陽と地球の間の距離が得られます.
$$
\begin{align*}
&\to \,\,\, a_1 = \left( a_1 - L \right) \left( \frac{T_1}{T_2} \right)^{2/3}
\end{align*}
$$
また,比較的遠い惑星についてもレーザーが拡散してしまうためその反射によって距離を測定することは困難ですが,公転周期を調べればケプラーの第三法則を適用することで距離を求めることができます.

https://commons.wikimedia.org/wiki/File:Saturn_PIA06077.jpg
https://en.wikipedia.org/wiki/File:Alien_aurorae_on_Uranus.jpg
年周視差
太陽によって重力的に束縛されていない,太陽系の外にある別の恒星などについては,ケプラーの第三法則を適用することはできません.そこで利用されるのが年周視差と呼ばれる現象です.

腕を伸ばして親指を立てた状態で,その親指を右目と左目のそれぞれで見てみると,遠くの物体に対して親指の位置が少しだけ変わるように見えます.これが視差です.同じように,私たちのいる地球は太陽の周りを公転していますから,季節によって比較的近くにある恒星の位置は少しだけ変わって見えます.これを年周視差と呼びます.

太陽と地球の間の距離はわかっていますので,恒星の位置の変化がわかると,三角測量によって恒星までの距離を計算することができます.初めて年周視差の観測に成功したのはドイツの科学者フリードリヒ・ヴィルヘルム・ベッセルで,はくちょう座61番星の年周視差がわずか0.3秒角程度であることを明らかにしました.

https://commons.wikimedia.org/wiki/File:Friedrich_Wilhelm_Bessel_(1839_painting).jpg
一般に年周視差はきわめて小さい値を取りますから,地上からの観測では大気のゆらぎの影響のため年周視差を精度良く測定することは困難です.そのため1989年,欧州宇宙機関ESAによって恒星の年周視差測定に特化したヒッパルコス衛星が打ち上げられ,地球から約150パーセク以内にある約12万個の恒星の年周視差が測定されました.

さらにその後継機として2013年にはガイア衛星が打ち上げられ,太陽と地球のラグランジュポイントの一つであるL2ポイントで観測が実施されました.ガイア衛星によってこれまでに10億個を越える恒星の年周視差がきわめて高い精度で測定され,その観測結果はさまざまな科学成果につながっています.

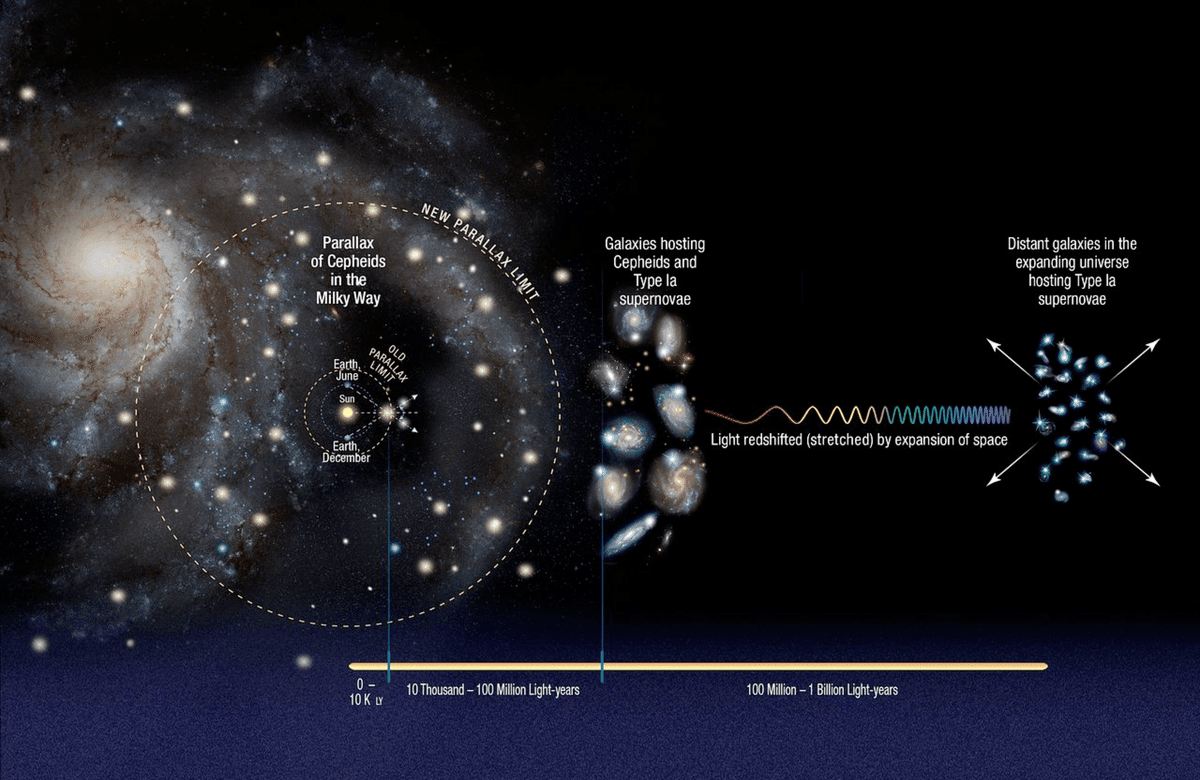
周期光度関係をもつ変光星
年周視差は遠い恒星ほど小さくなるため,3000光年を越える距離にある恒星に対しては測定することが難しくなります.さらに遠い天体までの距離を調べるためには,宇宙の距離はしごをまたひとつ上がる必要があります.

1900年代の初め,アメリカの天文学者ヘンリエッタ・スワン・リービットは,明るさが周期的に変化する変光星の中に,変光の周期と明るさが相関するものがあることを発見しました.これを周期光度関係と呼びます.この関係を利用すると,変光星の変光周期を観測することで,その本当の明るさを知ることができます.
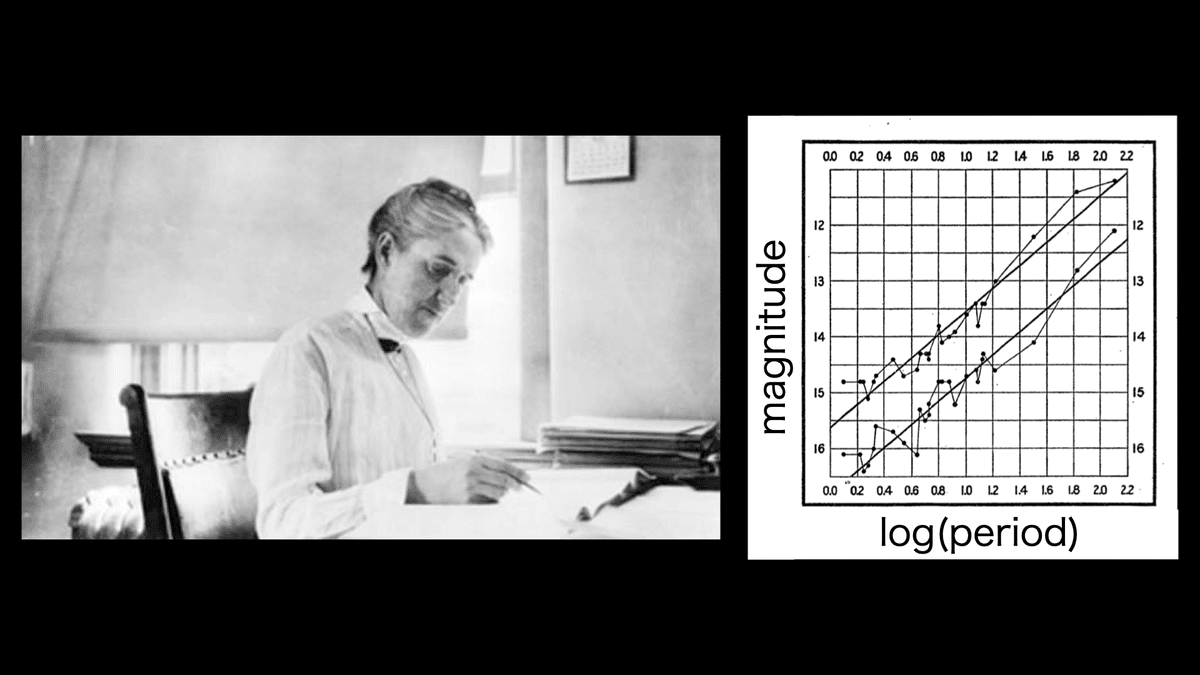
https://commons.wikimedia.org/wiki/File:HSLeavittHSCr13Fig2_1912.jpg
本当の明るさがわかっている天体のことを標準光源と呼びます.標準光源を観測すれば,その見かけの明るさと比較することで,その天体までの距離がわかります.たとえば,100ワットの電球を私たちからだんだん遠ざけると,その距離の2乗に反比例する形で電球の見かけの明るさは暗くなります.100ワット電球の本当の明るさがわかっている場合,見かけの明るさは距離の2乗に反比例することから,本当の明るさと見かけの明るさを比較することで100ワット電球までの距離を求めることができます.

変光星の周期光度関係を用いる方法は,明るさの変動を検出できれば良いため,年周視差を測定できないほど遠くにある天体であっても距離を求めることができます.1924年,アメリカの天文学者エドウィン・ハッブルは当時星雲と呼ばれていた天体にあるセファイド型変光星を観測してその距離を測定し,星雲が私たちの銀河系の外にある,別の銀河であることを示しました.そして,銀河系は宇宙全体に相当するものではなく,銀河系は宇宙に数多く存在している銀河のひとつに過ぎないことを明らかにしました.
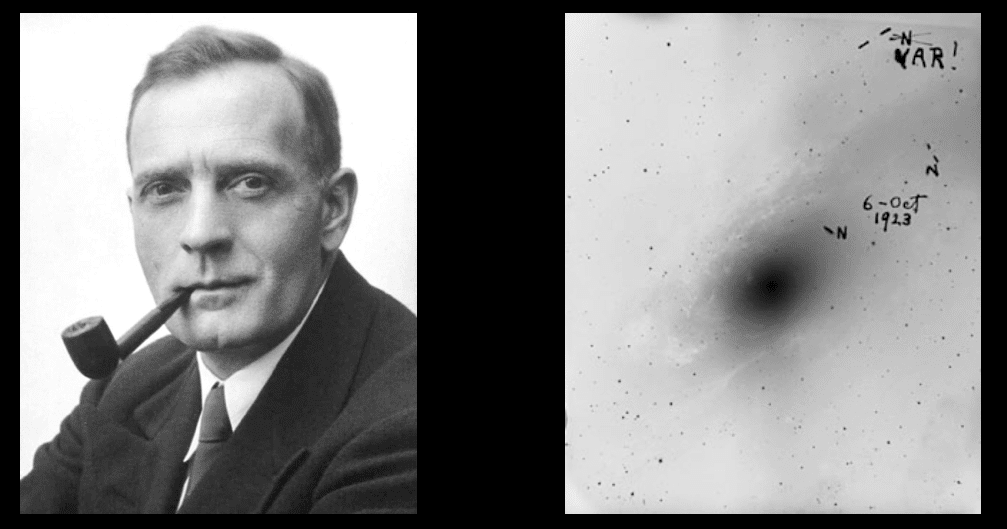
http://james.3zoku.com/kojintekina.com/physics/physics09060106.html
Ia型超新星
変光星は恒星の晩期に相当する天体ですが,明るさが限られているため,変光星の周期光度関係によって距離を求めることができるのは6000万光年ほど離れた天体までです.それより遠くにある天体までの距離を測るためには,さらに明るい標準光源が必要となります.そのひとつがIa型超新星です.
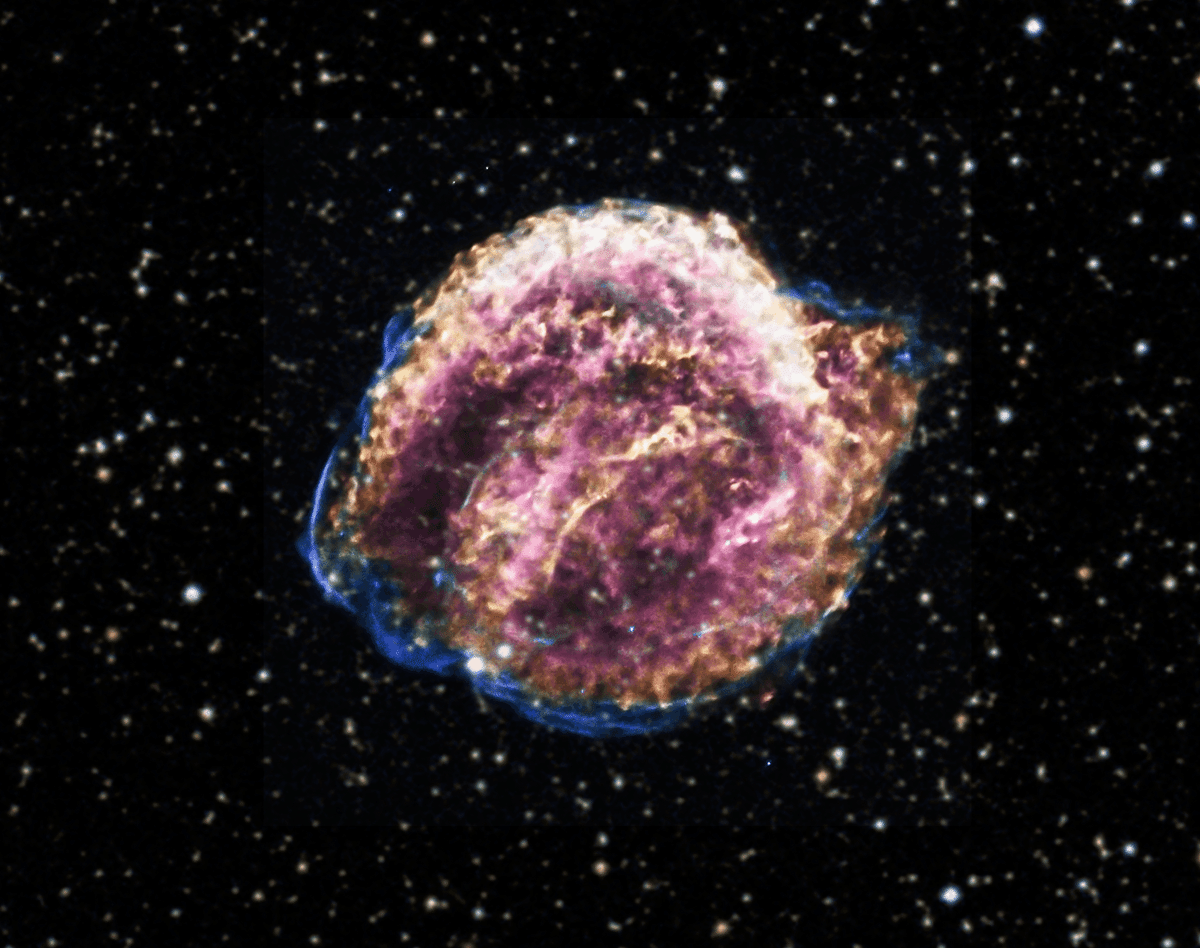
Ia型超新星は白色矮星が起こす超新星爆発です.白色矮星と赤色巨星からなる連星系において,肥大化した赤色巨星の外層が徐々に白色矮星へと降着していったり,白色矮星同士からなる連星系において合体が起きたりすることで,白色矮星が電子の縮退圧によって支えることのできる最大の質量であるチャンドラセカール限界を越えてしまうことで爆発すると考えられています.
これまでの観測から,Ia型超新星の明るさはほぼ一定であることが知られています.これは,チャンドラセカール限界がおよそ太陽質量の1.4倍とほぼ一定であるため,爆発の際のエネルギーもほぼ一定であるためと考えられています.このことから,Ia型超新星も標準光源として使うことができると期待されます.
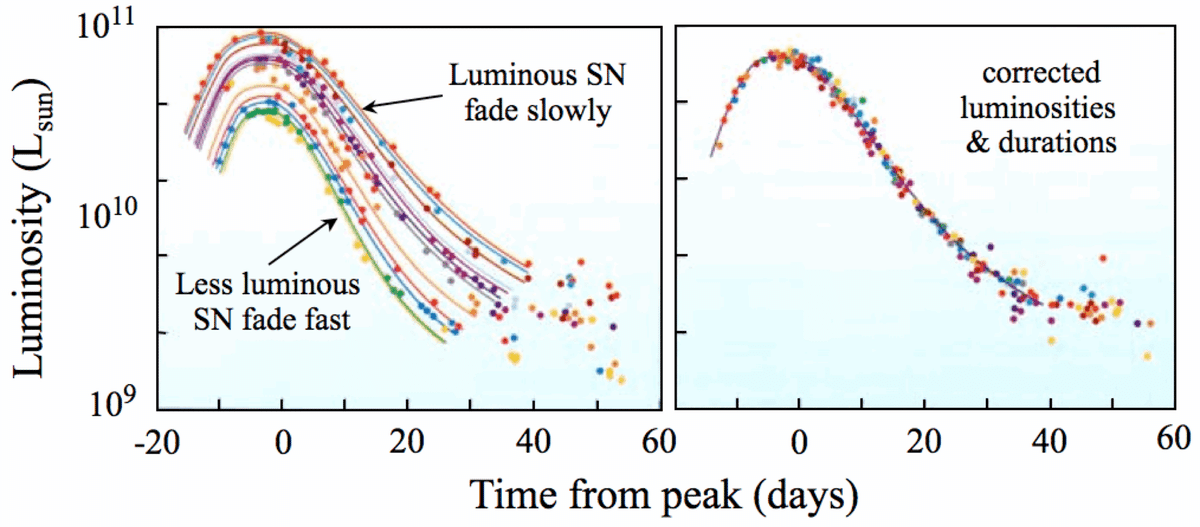
Ia型超新星は変光星よりかなり明るいため,より遠方にある天体まで距離を測定することができます.1990年代の終わりに二つの超新星観測チームが50億光年以上かなたにあるIa型超新星の観測結果をまとめ,宇宙は赤方偏移が0.5になるあたりで減速膨張から加速膨張へと切り替わっている,ということを発見しました.これは宇宙において「反発する重力」として作用するような未知の成分,いわゆるダークエネルギーの存在を示唆する結果として注目を集め,その起源は今も精力的に研究されています.
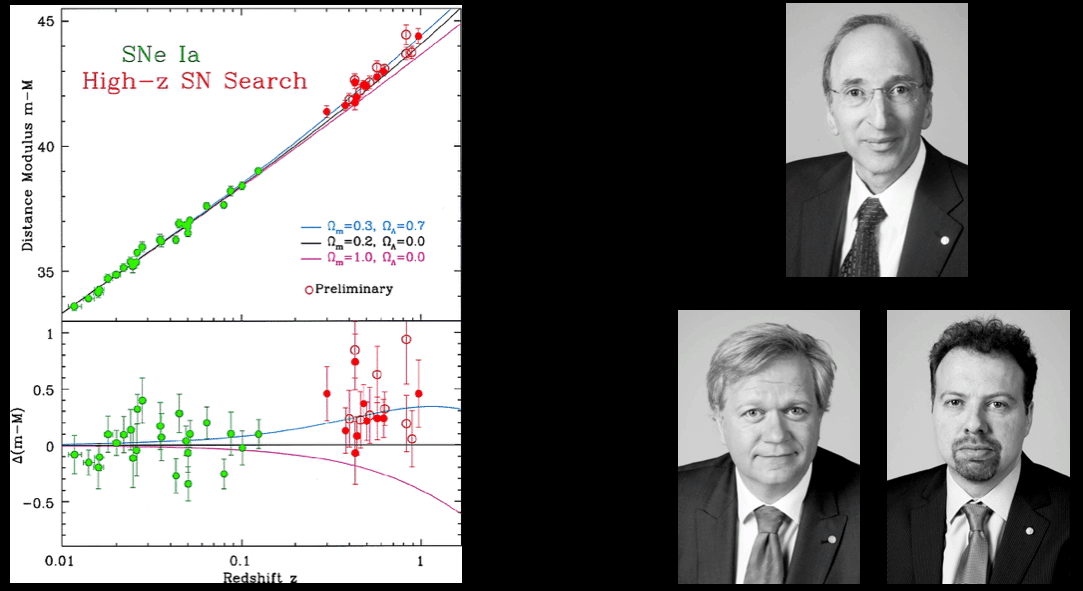
https://www.nobelprize.org/prizes/physics/2011/summary/
赤方偏移
変光星やIa型超新星といった標準光源が観測される天体はきわめて限られていて,宇宙にはそれ以外の天体の方が多く存在しています.実は,標準光源が観測されない天体に対しても,赤方偏移がわかれば,宇宙モデルを仮定することでその天体までの距離を計算することができます.現在知られている多くの遠方天体までの距離はこの方法で計算されています.

天体からの光が宇宙空間を伝播する際,宇宙膨張の影響を受けて波長が長くなります.アインシュタイン方程式から導かれる一様等方な宇宙の膨張史を記述するフリードマン方程式にもとにすると,天体までの距離と赤方偏移の関係を得ることができます.その関係式には密度パラメータや空間曲率パラメータがありますが,それらは宇宙マイクロ波背景放射などの観測によって良い制限が得られていますから,それらとともに天体の赤方偏移を代入することで,その天体までの距離が求められるというわけです.
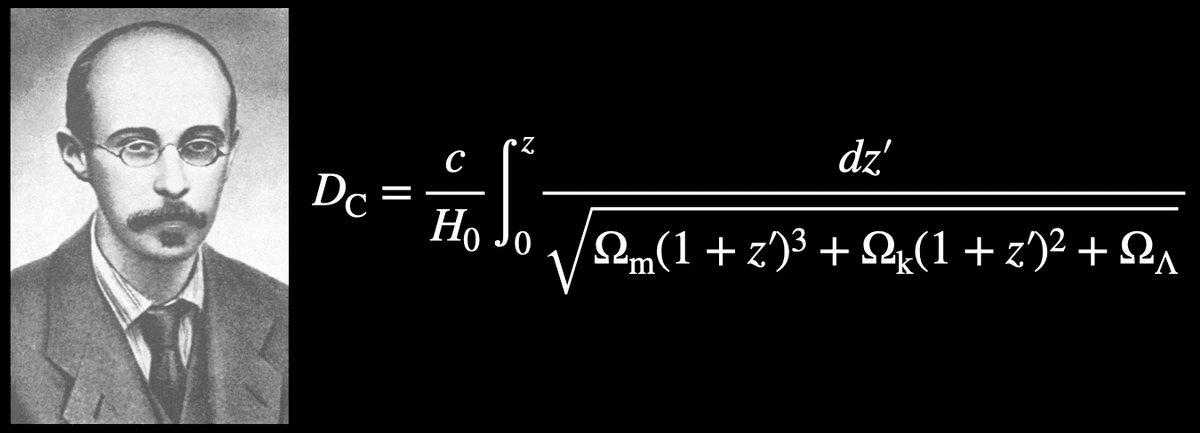
今回はさまざまな距離にある天体の距離測定法について紹介してきました.これらの他にも,重力レンズを用いる手法や重力波を用いる手法などもありますが,それぞれの手法は得意とする天体や距離範囲が異なるため,互いに相補的な関係にあると言えます.これらの手法はある程度確立されていると言ってよいでしょうが,まだ見つかっていない距離測定法は存在しているかもしれません.特に遠方宇宙でも使うことのできる新しい標準光源は,宇宙の膨張史そしてダークエネルギーの性質を明らかにする上で重宝されると考えられます.今後の研究によってさらなる進展があることを期待したいと思います.
参考
宇宙の距離梯子(Wikipedia)
https://ja.wikipedia.org/wiki/%E5%AE%87%E5%AE%99%E3%81%AE%E8%B7%9D%E9%9B%A2%E6%A2%AF%E5%AD%90
地学(数研出版)
https://amzn.to/3oR94cC
The Cosmic Ladder That Lets Us Map the Universe - SciShow Space
https://www.youtube.com/watch?v=rV-Z6jk9Fkw
遥か遠い天体までの距離はどうやって測っているの? - 宇宙ヤバイch
https://www.youtube.com/watch?v=OJqeKggMS0g
