
物理学概論:特殊相対性理論
日常生活で見られる物体の運動をよく説明できるニュートン力学では,運動というものは何か基準の物体を決めて,それに対する運動として捉えるという考え方がなされていました.より正確に表すと,ガリレイ変換と呼ばれる座標変換によって関連付けられるあらゆる慣性系において物理法則は変わらないという考え方で,ガリレイの相対性原理と呼ばれます.

慣性系というのは,静止していたり,向きを変えずに一定の速度で動いていたりする座標系のことです.たとえば,私たちは速度が一定の電車に立っていても,電車の動いている方向に力を感じることはありません.そのように,外から力を加えられていない物体が静止するか,もしくは等速直線運動を続けることは,慣性の法則として知られています.慣性系というのは,そうした慣性の法則が成り立つような系ということができます.

しかし電磁場を記述するマクスウェル方程式では電磁波の速さが一意に定まってしまい,電磁場に対してはガリレイの相対性原理は成り立たないことがわかりました.当初,マクスウェル方程式が厳密に成り立つのは絶対静止座標系のみであり,それ以外の慣性系ではガリレイ変換されたマクスウェル方程式が成り立つと解釈されていました.この場合,光の速さは慣性系に依存すると期待されますから,地球の公転運動を考慮するとその向きによって光の速さは異なると考えられます.ただ,そうした違いを検出しようとしたマイケルソン・モーリーの実験は失敗に終わり,それを受けてオランダの物理学者ヘンドリック・ローレンツらによっていくつかの理論が提唱されていました.

そんな中,ドイツ生まれの物理学者アルベルト・アインシュタインによって1905年に発表されたのが特殊相対性理論です.アインシュタインは,すべての慣性系において光の速さは変わらず秒速約30万キロメートルであること,そしてすべての慣性系において物理法則が同じ形で成り立つこと,という二つの原理をもとにした理論を展開しました.今回はその特殊相対論で説明される現象のうち,特に有名な「動いているものの時間がゆっくり進むこと」,そして「長さが縮むこと」について紹介をしていきます.

光速度不変の原理
そもそも光の速さが一定であるという考え方は,それまでの物理学における相対速度の考え方とは全く異なるものでした.たとえば,私たちが時速60キロメートルで走る自動車に乗っているとき,その横を新幹線が同じ方向に時速300キロメートルで走っているとします.このとき,新幹線の方が速いですから,新幹線は私たちを追い抜いていくことになります.そしてそのときの相対速度,すなわち自動車に乗っている私たちにとっての新幹線の速さは,300から60を引いて時速240キロメートルということになります.つまり同じ方向に動いている私たちから見ると,新幹線はやや遅く見えるのです.

しかし光速度不変の原理から,光についてはこうした相対速度の考え方が成り立たないことになります.光の速さは一定ですから,静止している人から見ても,動いている人から見ても,その速さは同じということになるためです.たとえば,光と同じ方向に動いている秒速10万キロメートルのロケットに私たちが乗っているとします.このとき,先ほどと同様の考え方で相対速度を計算すると,ロケットに乗っている私たちにとっての光の速さはロケットの速さの分だけ遅く見えそうです.しかし,光速度不変の原理から,ロケットに乗っている私たちから見た光の速さも,変わらず秒速約30万キロメートルということになります.

実は,秒速約30万キロメートルというのは,この世界における速さの上限に相当します.光子は,モノの動かしにくさに対応する物理量である質量がゼロであるため,上限の速さである秒速約30万キロメートルで動くことができるというわけです.

時間の遅れ
光速度不変の原理と,すべての慣性系で物理法則が変わらないとする特殊相対性原理をもとにすると,簡単な考察から動いている系での時間がゆっくり進むように見えるという,一見すると不思議な結論が得られます.それまでの物理学では,日常生活での経験をもとに,時間はみな同じものを共有していると考えられていました.しかし実際は,速度の大きい慣性系における時間はゆっくりと進むように見えることが示されます.
簡単のため,天井が非常に高い仮想的な電車を考えます.電車は一定の速度$${V}$$で運動しています.その電車の床に光源を置き,天井に検出器を置きます.そして,光源から放たれた光を天井で検出するという実験を行うとします.

まずはこの実験を電車の中で観測する場合を考えます.光が放たれてから天井の検出器に到達するまでの時間を$${T_{\rm in}}$$とおきます.光の速さを$${c}$$と表すことにすると,光の移動した距離,すなわち光源から天井までの距離は$${c T_{\rm in}}$$と表されます.

一方,この実験を電車の外から観測する場合を考えます.このとき,電車が動いている分だけ光の移動距離は変わります.光が放たれてから天井の検出器に到達するまでの時間を$${T_{\rm out}}$$とおくと,光の移動した距離は$${c T_{\rm out}}$$と書けます.そして,光源から天井までの距離は$${c T_{\rm in}}$$であり,光が天井に到達するまでに電車が移動した距離が$${V T_{\rm out}}$$であることに注意すると,三平方の定理より,
$$
\begin{equation*}
(c T_{\rm out})^2 = (c T_{\rm in})^2 + (V T_{\rm out})^2
\end{equation*}
$$
が成り立ちます.

三平方の定理から得られた等式を変形して$${T_{\rm in}}$$について解くと
$$
\begin{align*}
(c T_{\rm in})^2 &= (c T_{\rm out})^2 - (V T_{\rm out})^2\\
\to \,\,\,
T_{\rm in}^2 &= T_{\rm out}^2 - \left( \dfrac{V}{c} \right)^2 T_{\rm out}^2 \\
\to \,\,\,
T_{\rm in} &= \sqrt{1 - \left( \dfrac{V}{c} \right)^2} T_{\rm out}
\,\,\,\,\,\,\,\, (\because T_{\rm in} > 0)
\end{align*}
$$
を得ます.右辺で$${T_{\rm out}}$$にかかっているルートの部分は必ず1より小さいですから,これより$${T_{\rm in} < T_{\rm out}}$$である($${T_{\rm out}}$$は$${T_{\rm in}}$$より大きい)ことが言えます.つまり,電車の外から見た時間は,電車の中での時間と比べてゆっくり進んでいるように見えることになります.これが特殊相対性理論における時間の遅れです.
ただ,普段目にするような物体の速さは光の速さと比べると十分に遅いため,こうした時間の遅れを私たちが体感することはほぼありません.そのため,日常生活にもとづく直観からは理解することが難しいと感じるかもしれませんが,光速度不変の原理と特殊相対性原理をもとにした簡単な考察によって,こうした不思議な現象を理解することが可能となるのです.

空間の縮み
時間だけでなく空間についても,日常生活にもとづく直観では理解することの難しい現象が起こります.ここでは一定の速度$${V}$$で走る電車を,レールの端から端まで動かすような実験を考えます.

まず,この実験を電車の中から観測します.電車がレールの端から端まで動くのにかかった時間を$${T_{\rm in}}$$とします.このとき,電車の中から見たレールの長さを$${L_{\rm in}}$$とおくと,電車の速さは$${V = L_{\rm in} / T_{\rm in}}$$と表されます.
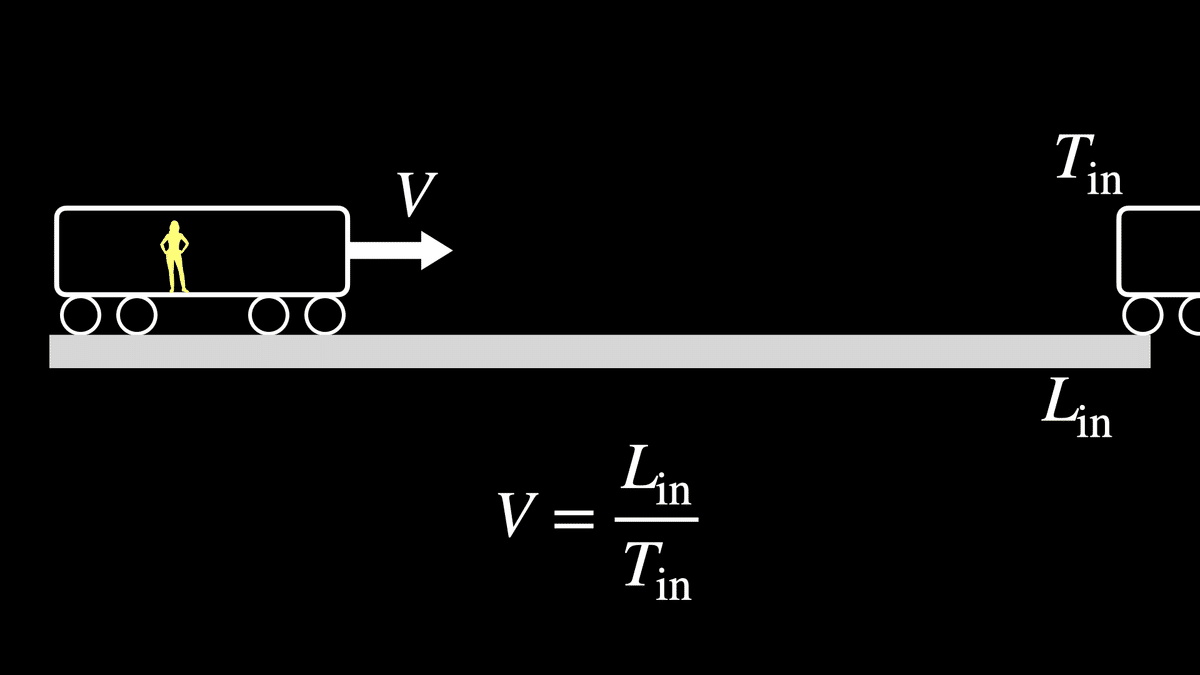
一方,この実験を電車の外から観測する場合を考えます.このとき,電車がレールの端から端まで動くのにかかった時間を$${T_{\rm out}}$$とし,電車の外から見たレールの長さを$${L_{\rm out}}$$とおくと,電車の速さは$${V = L_{\rm out} / T_{\rm out}}$$と書くことができます.

電車の速さはどちらにとっても同じはずですので,これらより
$$
\begin{equation*}
V =\dfrac{ L_{\rm in} }{ T_{\rm in} } = \dfrac{ L_{\rm out} }{ T_{\rm out} }
\end{equation*}
$$
が得られます.これを$${L_{\rm in}}$$について解くと次のようになります.
$$
\begin{equation*}
L_{\rm in} = \dfrac{ L_{\rm out} }{ T_{\rm out} } T_{\rm in}
\end{equation*}
$$
ここで先ほど見た特殊相対性理論における時間の遅れの効果を$${T_{\rm in}}$$に代入すると,
$$
\begin{align*}
L_{\rm in} &= \dfrac{ \sqrt{1 - \left( \dfrac{V}{c} \right)^2} T_{\rm out} }{T_{\rm out}} L_{\rm out} \\
&= \sqrt{1 - \left( \dfrac{V}{c} \right)^2} L_{\rm out}
\end{align*}
$$
が導かれます.ここで,右辺で$${L_{\rm out}}$$にかかっているルートの部分は必ず1より小さいですから,これより$${L_{\rm in} < L_{\rm out}}$$である($${L_{\rm out}}$$は$${L_{\rm in}}$$より大きい)ことが言えます.つまり,電車の中から見たレールの長さは,電車の外で見ている長さと比べて短いことになります.レールに対して動いている慣性系から見ると,レールの長さが縮んで見えることになります.これが,特殊相対性理論における空間の縮みという現象で,ローレンツ収縮と呼ばれます.
実際の例:ミューオン
こうした現象は現実離れしているように感じるかもしれませんが,例えば光速に近い速さで運動する粒子の振る舞いを理解するために不可欠です.代表的な例が,地表に降り注いでいるミューオンです.

私たちの地球は大気によって覆われていますが,大気には宇宙からたくさんの宇宙線が飛び込んできています.宇宙線が大気中の粒子にぶつかると,壊れて他の粒子に変わることがあります.そのときに出てくるのがミューオンという粒子で,実際ミューオンは地表にたくさん降り注いでいることが知られています.

ただ,ミューオンは非常に寿命の短い粒子で,平均寿命$${\tau}$$は2x10のマイナス6乗秒程度しかありません.ミューオンの質量はとても小さいため,ほぼ光の速さで動いていますが,それでもこの短い寿命で移動できる距離は限られています.平均的な移動距離をおおまかに計算すると,
$$
\begin{equation*}
c \tau \simeq (3 \times 10^8) \times (2 \times 10^{-6})
= 600 \, {\rm m}
\end{equation*}
$$
という値が得られます.大気圏はこれより厚いですから,こうした単純な計算によるとミューオンの大部分は地表に届くまでに崩壊することになってしまい,地表にたくさん降り注いでいることに反してしまいます.
この矛盾は相対論的な効果を考慮することで解消されます.例えば地上の私たちからミューオンを見ると,ミューオンはほぼ光の速さで動いているため,ミューオンの時間はゆっくりと進んでいるように見えます.そのため,その分だけ寿命が伸びているように見え,地上へと到達できることになります.

見方を変えてミューオンの立場で考えると,光速に近い速さで動いているため周囲の空間が縮んで見えることになり,地表までの距離も短く見えることになります.そのため,ミューオンは地表へと到達できるわけです.

今回は特殊相対論で説明される現象のうち,いわゆる時間の遅れと空間の縮みについて簡単に紹介しました.簡単な議論をもとに,時間や空間に対して私たちの日常生活にもとづく認識とは異なる本当の姿が浮かび上がりました.他にも特殊相対論からは質量とエネルギーの等価性,すなわちエネルギーと質量は同じものの異なる現れ方であることが導かれます.アインシュタインによって発表された特殊相対論はその後,重力場を記述する理論である一般相対論へとつながっていくことになります.

参考文献
『難しい数式はまったくわかりませんが、相対性理論を教えてください!』
https://amzn.to/34AHycC
相対性理論(基礎物理学選書27)
https://amzn.to/3hZB623
この記事が参加している募集
この記事が気に入ったらサポートをしてみませんか?
