scikit-learn 回帰分析 - リッジ回帰

今日のMusic : BBC Pete Tong, 

参考：(1), (2), (3), (4)

ここからは参考(1)に沿ってボストンの家の値段データをRidge Regreesionしてみる。

1. Always start from checking the data! - 先ずはデータのチェック!

"preprocessing.scale" で「平均を0・分散を1」に標準化し、

Gaussian with zero mean and unit variance. - 6.3 Preprocessing

そのあとtest_sizeを30%と設定。random_stateは何でも良いが、次回同じ解析をしたい時には同じく10を使うこと。

ここで、データを理解するため、それぞれの変数がどういう意味かチェック。ここにあった説明をGoogle翻訳で(オレンジはGoogleが勝手に日本語に変更したので元を選んだらこうなった)：

相関もチエック。

前回同様に、eigenvalue（固有値）を見てみる。上の相関マップで相関があるようには見えなかったが、固有値も０に近い(<0.01)値はない。

全てのvariableを解析に使用することとする。

ちなみに、データが大量にある時には、明らかな相関のあるvariableを除きたいときがあるかもしれない。そんな時には、PCA(Principal Component Analysis 主成分分析)を行う。

2. Check OLS - 最小２乗回帰

Ridge & Lassoとの比較のため、予測の精度を検証する値である、　R^2決定係数と、MSE(Mean Squared Error 平均２乗誤差)を出しておく。

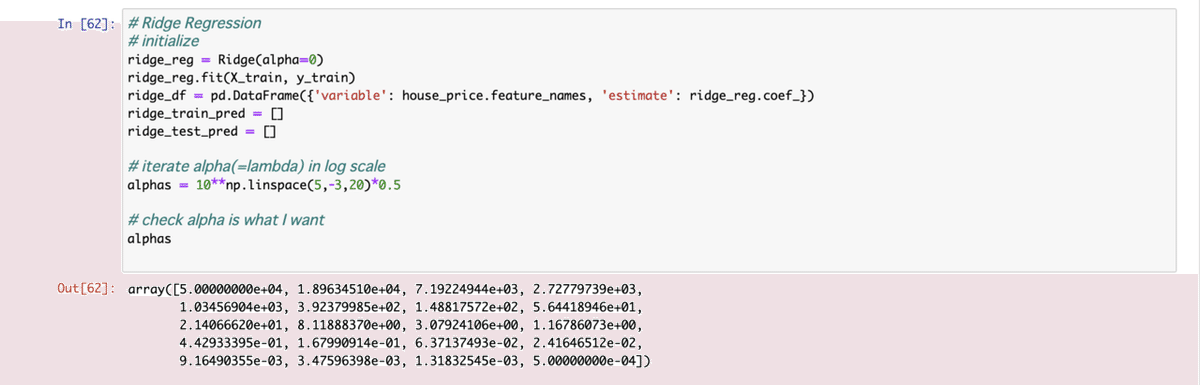
3. Ridge Regression - リッジ回帰

上と同じデータでリッジ回帰の初期設定と、正則化項のラムダ（アルファとも呼ばれる）の範囲をlog scale(対数)で設定。

リッジ・ラッソの式の日本語での説明は例えばここにあるので省略するが、ラムダ x リッジでは重み(w)の二乗・ラッソではabs(重み) のsum(計)になるのでRidge をL2 regularization (正則化)、LassoをL1 regularizationと呼ぶ。

リッジ・ラッソでOLSの項に正則化の項を加えることで何をするか？

overfitting(過学習)を抑制する。モデルが複雑になるほど、訓練用データ(train)へのフィットがよくなるのは自明だが、その他のデータに対しては予測(pred)と目標(target)の差が大きくなってしまう。

このoverfittingという現象を抑えたい　→　逆に、モデルを鈍らせる・単純化させたい　→　各predictor variable (予測変数)の wight(w, beta, regression coefficient ともいう) をshrink(小さく)したい　→　どうするか？　→　そうだ、weightにpenalty (ペナルティ)を与えよう　→　lambdaという係数を掛算すれば、lambdaが大きくなるにつれ、各weight(regression coef.)は小さくなる

リッジ・ラッソでよく目にする以下のようなplotは、上記のlambdaがおおきくなるにつれ、各regression coef. がshrink(縮小)されていくことを表す。

lamda vs. MSE(平均２乗誤差)もplotしておく。

ここで、必要なのは、cross-validationのチェック。

統計データの解析や機械学習では、bias-variance (偏りと分散)のトレードオフや、ジレンマという言い方まで目にするが、リッジ回帰の式では(2)より、

と導かれる。lambdaが大きなるにつれ、係数がlambdaのbiasは大きくなり、varianceが小さくなる(lambdaが逆行列の中なのでlambdaは分母にくる)事が見て取れる。

では、lambdaのちょうど良い値はどうやって検証する？　この方法の一つとしてcross-validation (交差検証)がある。交差検証されたsquared residuals(２乗残差)のsum(計)を最小化するlambdaを選ぶ、という方法。sum of squared residuals (SSR)とかresidual sum of squares (RSS)とか sum of squared estimate of errors (SSE)とか、色々な呼び方があるらしい。

ちなみに、このwikipediaページのRegressionの項目には

The term mean squared error is sometimes used to refer to the unbiased estimate of error variance: the residual sum of squares divided by the number of degrees of freedom.

とあるので上にあるMSEのplotはRSS/Nとなる。

(以下6/11追加)

plotからではベストなlambda(or alpha)の値はわからないので、Ref(4)にあるようにRigdeCVを使って求める。

Ridge Regression結果 : lambda = 0.009, MSE=29.27, r^2=0.700