
[数学コラム] 素数の無限性
初めて数学についてコラムを書きます。
私は大学・大学院と応用数学を学んでいて、数学が好きなんです。大学院を修了してから、なかなか数学を学べていないので、コラムを書くことが数学を学ぶきっかけになればいいなと思っています。
今回は「素数が無限に存在することの証明」について書きます。「素数が無限に存在することの証明」は、ユークリッドというギリシャの数学者が紀元前3世紀頃に書いた「原論」に載っていることでも有名です。
今回紹介する証明方法のみそは「背理法」です。背理法は高校数学で習うもので、多くの人が通ったものだと思います。まず、背理法とはどのようなものかについて話そうと思います。
背理法とは「証明したい命題の否定命題について考え、その否定命題の矛盾を導き出し元の命題を証明する方法」と言えます。少し難しいですよね。
ここで問題になるのが「証明したい命題の否定命題をどう考えればいいのか?」です。そのことを説明するには論理学の力を少し借ります。
命題は基本的に「AならばB」という形で表わすことができます。しかし、「AならばB」の否定をすぐに導き出すのは容易ではないです。そのためには「AならばB」を真理値表で表わすことが第1ステップです。真理値表は以下の通りです。
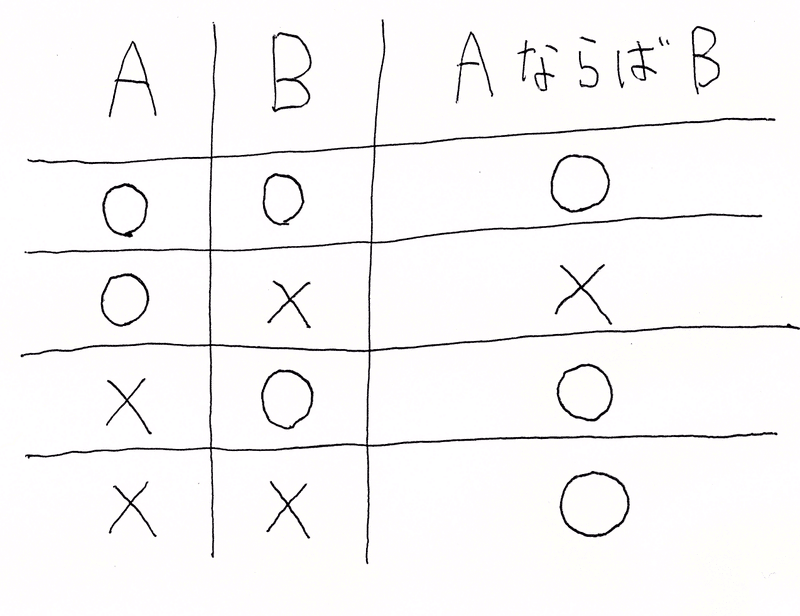
〇は正で×は誤です。まず、仮定であるAが正で結論であるBも正のとき「AならばB」が正になることは分かりやすいかなと思います。次に、Aが正でBが誤のときは仮定は正しいけど結論が誤まりなので「AならばB」は誤です。さらに、Aが誤でBが正のときは仮定に関わらず結論が正しいので「AならばB」は正です。最後のAもBも誤のとき「AならばB」が正になる、のはわかりにくいです。僕自身もあまりしっくりした説明ができないので、そういうものだと思っていただけるとありがたいです(笑)。
次に否定命題を考えます。でも、先ほども述べた通り、命題「AならばB」の否定命題というのは容易に導き出すことはできません。そこで先ほどの真理値表が活きてきます。
まず「AならばB」を別の言い方で表すことを考えます。結論からいうと「AならばB」は、「Aでない、または、B」と言い換えることができます。なぜなら「AならばB」と「Aでない、または、B」の真理値表が一致するからです。
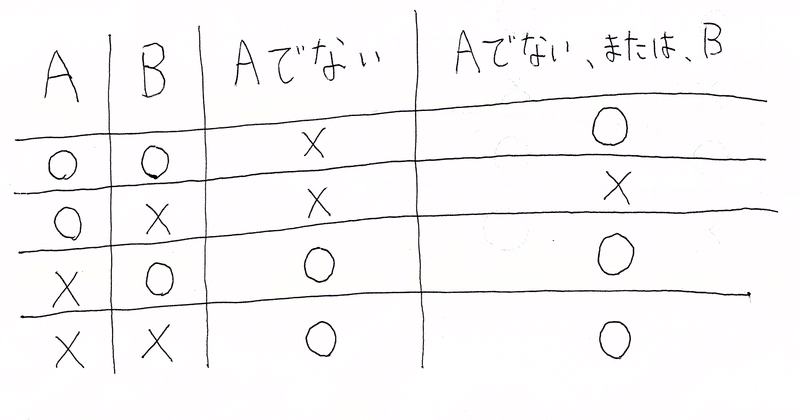
ここでの真理値表の正誤についての説明は割愛します。高校数学の範囲なので。(もしわからなかったらコメントしていただければお答えできる範囲で答えます。)
この真理値表を見てわかるとおり「Aでない、または、B」の正誤が「AならばB」の正誤と一致していますよね。なので「AならばB」と「Aでない、または、B」を同一視することができます。
よって、やっと命題「AならばB」の否定命題を考えことができます。「AならばB」の否定はつまり「Aでない、または、B」の否定なので、それは「A、かつ、Bでない」となります。これはド・モルガンの法則ですね。
したがって、命題「AならばB」を背理法で証明するには「A、かつ、Bでない」を考え矛盾を導き出せばいいのです。
背理法の説明で長くなりましたね。ようやく「素数が無限に存在することの証明」の説明に入ることができます。
「素数が無限に存在する」を言い換えると、「整数Xが素数ならばXよりも大きい素数が存在する」と言えます。そして、その否定は、先ほど考えた通りに考えると「整数Xが素数、かつ、Xよりも大きい素数が存在しない」と言えます。簡単に言うと「最大の素数Xが存在する」ということです。これについて、矛盾を導き出せばよいのです。
以下、証明になります。

この証明では整数の素因数分解の可能性や一意性について自明のものとしています。素因数分解の可能性や一意性について詳しく知りたい方は整数論の本や代数学の本を読むことをおすすめします。(僕は松坂和夫「代数系入門」で学びました。)
以上、「素数が無限に存在することの証明」に関するコラムでした。なるべく易しく説明したつもりでしたが、振り返ると、数学にあまり触れていない方には難しい部分もあったかもしれません。そこはご了承ください。
また数学のコラムを書けたらなと思っています。最後まで読んでくださりありがとうございました。
この記事が気に入ったらサポートをしてみませんか?
