トランジスタ、hパラメータ

公開状態にしてますが、編集中です。
間違いや表記ゆれがあります。

トランジスタの機能は、増幅・スイッチングがある。
試験では、特に増幅の特性に関する問題が出題されるので、確認をする。

院試で使用した電子回路の教科書

電子回路・アナログ回路の単位を取ったけど忘れた人

院試で必要となる基本知識を身に着けて、
旧帝大の過去問を解き切るレベルまでに到達させる。

よくわかる電子回路の基礎

多くの参考書で省略される数式の導入が詳細に書かれているので、
暗記から解放される。

このテキストを読んでから過去問を解くことを薦める。

トランジスタの接地

接地（GND）によって、エミッタ接地、コレクタ接地（エミッタホロワ）など名称がある。

エミッタ接地は電流・電圧・電力増幅を大きくさせて、
入出力抵抗が普通の大きさになる。

その他は、ほぼ１。逆に増幅が小さくなる時がある。
実用性と試験の出やすさは、エミッタ接地トランジスタである。

バイアス回路

トランジスタのベース-エミッタ間の電圧$${V_{BE}}$$は、
pn接合ダイオードとみなすことができる。

要するに、入力電圧が負であると、ベース電流は流れない。
問題を解決するには、直流電流を流せばよい。

トランジスタのベース-エミッタ間の電圧$${V_{BE}}$$は一般的に、$${0.7V}$$前後であり、これよりも低い入力電圧は増幅できない。
※温度上昇で電流増幅率$${h_{FE}}$$は大きく増幅するが、
$${V_{BE}}$$は低下する。

代表的なバイアス回路は、固定バイアス回路、自己バイアス回路、電流帰還バイアス回路がある。

固定バイアス回路

$${I_B=\displaystyle \frac{E_C-V_{BE}}{R_B}}$$

$${I_C=h_{FE}\displaystyle \frac{E_C-V_{BE}}{R_B}}$$

この式から、固定バイアス回路は温度の影響を強く受ける。

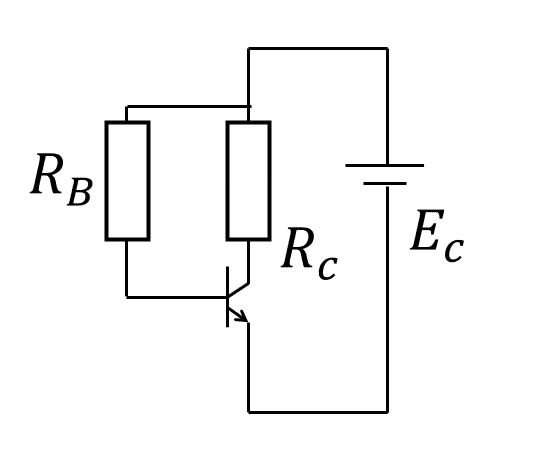
自己バイアス回路

別名：電圧帰還バイアス回路

固定バイアス回路と異なることは、$${R_B}$$の位置である。

$${I_B=\displaystyle \frac{V_{CE}-V_{BE}}{R_B}}$$

$${V_{CE}=E_C-I_CR_C}$$
※$${I_B<<I_C}$$とした。
この式から、$${I_C}$$が大きくなると$${V_{CE}}$$が小さくなる。

$${I_B=\displaystyle \frac{(E_C-I_CR_C)-V_{BE}}{R_B}}$$
$${V_{CE}}$$の式から、$${I_C}$$が大きくなると、$${I_{B}}$$が小さくなる。

しかし、$${I_C=h_{FE}I_B}$$だから、
$${I_{B}}$$が小さくなると、$${I_C}$$が小さくなる。
この抑制効果が自己バイアスに相当する。

固定バイアスよりも安定度は高いが、
安定度は高くするには、$${R_C}$$を大きくしなければならない。

電流帰還バイアス回路

ポイントは、$${R_A}$$の電圧を$${E_C}$$の分圧

$${V_A=\displaystyle \frac{R_A}{R_A+R_B}E_C}$$

閉回路より、$${V_A=V_{BE}+R_EI_E}$$
$${V_{BE}=V_{A}-R_EI_E}$$

$${V_{BE}}$$が低下すると、$${I_B}$$は低下して、$${I_C}$$は低下する。

$${R_E}$$を大きくするほど、安定度は高まるが、出力電圧は小さくなる。
一般的に$${V_E}$$は$${E_C}$$の10~20%となる$${R_E}$$を設定する。

抵抗を４つ使い、消費電力が大きくなることが欠点。

等価回路（hパラメータ）

そもそも、Hパラメータは何なのか？
何に使うのか？

定義

Hパラメータは、トランジスタの特性を表し、
2端子対回路において行列で定義される。
※箱$${h}$$は回路の要素でブラックボックスを示している。

この2端子対回路をH行列式（ハイブリット行列）で定義します。

$${\begin{pmatrix} v_i\\ i_o \end{pmatrix}=\begin{pmatrix} h_{11} & h_{12} \\ h_{21} & h_{22} \end{pmatrix}\begin{pmatrix} i_i\\ v_o \end{pmatrix}}$$

計算をすると、
$${v_i=h_{11}i_i+h_{12}v_0}$$
$${i_o=h_{21}i_i+h_{22}v_0}$$

$${(1)v_o＝0}$$
$${h_{11}(=h_i)=\displaystyle \frac{v_i}{i_i}}$$　（入力インピーダンス）
$${h_{21}(=h_f)=\displaystyle \frac{i_o}{i_i}}$$　（電流増幅率）

$${(2) i_i=0}$$
$${h_{12}(=h_r)=\displaystyle \frac{v_i}{v_o}}$$　（電圧帰還率）
$${h_{21}(=h_o)=\displaystyle \frac{i_o}{v_o}}$$　（出力アドミタンス）

fは順方向（foward）
r は逆方向（reverse）
iは入力（input)
oは出力（output）

その後ろにエミッタ・ベース・コレクタそれぞれの接地で添え字が変わる。
$${h_{ie},h_{rb},h_{oc}}$$など

小信号等価回路

Hパラメータを使って、トランジスタの等価回路を作成する。

初めに、トランジスタのみを考える。
冒頭の抵抗やバイアス電圧等を全て取り除いた回路である。

２式を満たす回路を作成します。
$${v_i=h_{ie}i_i+h_{re}v_o}$$
$${i_o=h_{fe}i_i+h_{oe}v_o}$$

一度トランジスタは増幅特性を持つことを思い出してみる。
つまり、小さい（入力）電流・電圧成分が、
大きい（出力）電流・電圧成分になる。

このことから、
入力インピーダンス$${h_{ie}}$$と電流増幅率$${h_{fe}}$$は大きい。
電圧帰還率$${h_{re}}$$と出力アドミタンス$${h_{ie}}$$は十分小さい。

したがって、指示があれば(重要)、
電圧帰還率$${h_{re}}$$と出力アドミタンス$${h_{ie}}$$は無視できる。

煩雑な計算が必要になるが、言及されていなければもちろん無視できない。これが、Z/Y/K行列ではなく、H行列にするメリットである。

ただし、BCE接地で、電流は増幅するが、電圧はしないということはある。

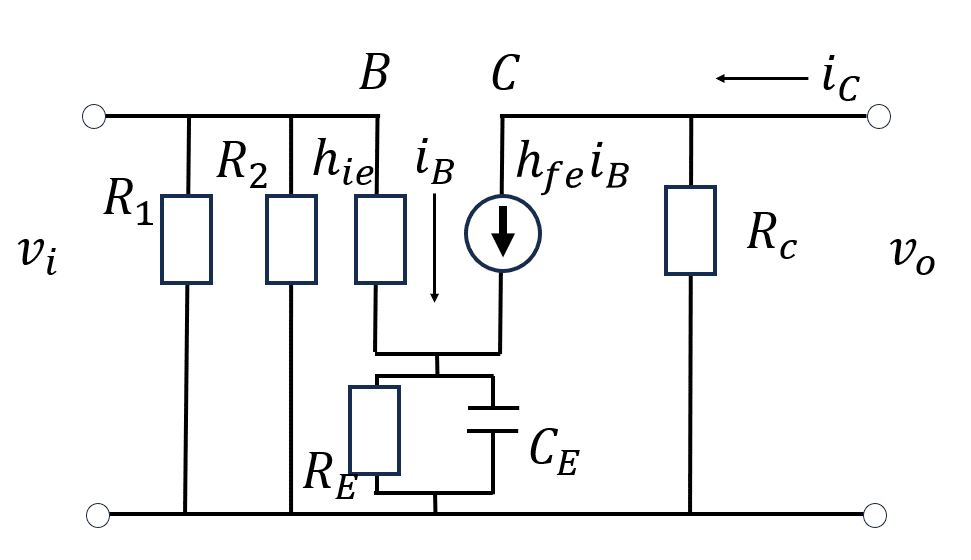
バイパスコンデンサ

図に示した$${C_E}$$は、バイパスコンデンサという。
安定抵抗$${R_E}$$で交流成分が低下し、出力電圧が低下することを防ぐ役割。

また、$${C_1,_2}$$は、結合コンデンサという。
直流成分を遮断する目的で使用される。

増幅回路から交流成分のみ取り出す。
つまり、コンデンサと直流電源$${E_c}$$は短絡。

$${C_E}$$を短絡させると$${R_E}$$は開放するので、
等価回路では考慮しなくてよい。

コンデンサ短絡

$${v_i=h_{ie}i_b}$$
$${v_o=-R_ci_c}$$
$${i_c=h_{fe}i_b}$$

したがって、電圧増幅率$${A_v}$$は、
$${A_v=\displaystyle\frac{v_o}{v_i}=-\displaystyle\frac{h_{fe}R_c}{h_{ie}}}$$

$${R_1,R_2}$$は、関係ないことに注意する。
入力インピーダンス$${Z{in}=R_1//R_2//h_{ie}}$$である。
出力インピーダンス$${Z{out}=R_3}$$である。

低域遮断周波数

コンデンサ短絡させた回路は、中域遮断周波数である。
電圧利得が3dB低下する周波数２つの内、低いものを低域遮断周波数と呼ぶ。

入力・出力結合コンデンサ考慮

初めに、入力結合コンデンサのみを考える。

今回は、$${R_1,R_2}$$も考慮する必要がある。
※試験で$${R_1,R_2>>h_{ie}}$$と指定している場合は、
$${R_1,R_2}$$は無視。（並列で逆数だから0になる）

計算が煩雑になるので、ここでは$${R_1//R_2}$$を無視して、低域遮断周波数$${f_{C1}}$$を求める。

$${|A_{C1}|=\displaystyle\frac{h_{fe}R_c}{h_{ie}}\displaystyle\frac{1}{ \sqrt{1+(\displaystyle\frac{1}{\omega C_1h_{ie}})^2}}}$$

中域周波数から、電圧利得が3dB低下した周波数が低域・高域周波数になる。

$${20 \log_{10}|A_{C1}|=20 \log_{10}|A_{v}|-3}$$

$${\displaystyle\frac{|A_{C1}|}{|A_v|}=10^{-0.15}=\displaystyle\frac{1}{\sqrt{2}}}$$

ゆえに、
$${\omega C_1h_{ie}＝１}$$

$${f_{c1}＝\displaystyle\frac{1}{2\pi C_1h_{ie}}}$$

同様に、出力バイパスコンデンサの場合は、
$${f_{c2}＝\displaystyle\frac{1}{2\pi C_2(R_c+R_i)}}$$
※$${R_i}$$は出力側に接続した入力抵抗を考慮した場合。

バイパスコンデンサ考慮

$${v_i=i_bh_{ie}+i_eZ_E=ib(h_{ie}+h_{fe}Z_E)}$$
※$${i_e \simeq i_c}$$とした。

出力電圧は、はじめと同じ。
$${v_o=h_{fe}R_ci_b}$$

計算をすると、
$${f_{CE}＝\displaystyle\frac{h_{fe}}{2\pi C_Eh_{ie}}}$$

高域遮断周波数

高域では、ベースコレクタ間の接合容量$${C_{oe}}$$を考慮しなければならない。
さらに、ベースコレクタ間電流が流れる。

$${i_{cb}=j \omega C_{ob}(v_i-v'_o)=(1-|A_v|)v_i}$$
$${C_i=C_{ob}(1+|A_v|)}$$

これより、入力側から見ると、$${C_{oe}}$$は、静電容量$${C_i}$$が接続されていると考えられる。（ミラー効果）

$${v_i}$$では考えにくいので、テブナンの定理で電流源に

この場合は、電流比$${\displaystyle\frac{i_b'}{i_b}}$$から求める。

$${\displaystyle\frac{i_b'}{i_b}＝\displaystyle\frac{1}{ \sqrt{1+( \omega C_iR)^2}}}$$

$${f_{ci}＝\displaystyle\frac{1}{2\pi C_iR}}$$
※$${R=R_1//R_2//h_{ie}}$$

負帰還増幅回路

前章のバイパスコンデンサ$${C_E}$$を取り除いた回路

等価回路から、負帰還増幅回路の電圧増幅度$${A_{vf}}$$を求める。

入出力電圧は、
$${v_1=v_i+Fv_o}$$
$${v_o=-|A_v|v_1}$$
※$${v_1}$$は、増幅回路の入力電圧

従って、負帰還増幅回路の電圧増幅度$${A_{vf}}$$は、

$${A_{vf}=\displaystyle\frac{v_o}{v_i}=-\displaystyle\frac{|A_v|}{1+|A_v|F}}$$

電圧に注目して、帰還率$${F}$$を求める。

$${F=\displaystyle\frac{|v_f|}{|v_o|}=\displaystyle\frac{|i_ER_E|}{|i_CR_C|} \simeq \displaystyle\frac{R_E}{R_C}}$$

増幅回路の電圧増幅$${A_v}$$は、

$${A_v = \displaystyle\frac{h_{fe}R_3}{h_{ie}} }$$

$${A_{vf} \simeq \displaystyle\frac{-R_3}{R_4}}$$

よくわかる電子回路の基礎