存在しない数?~虚数は定義するのに、1÷0は定義しないわけ~
虚数は「存在しない数」とよく言われます。現実世界ではイメージがしにくいため、苦手意識を持つ人も少なくないでしょう。
一方で、$${\frac{1}{0}}$$ は定義できない(存在しない数)として、習いますよね。
「いや、虚数みたいに定義すればいいじゃないか」
そんな疑問を一緒に考えてみましょう。
結論から
おそらく、虚数も$${\frac{1}{0}}$$も、研究していた数学者はいたのでしょう。そのような研究の結果、虚数だけが生き残りました。
なぜでしょうか?
その理由は単純です。
「虚数は役立つけど、$${\frac{1}{0}}$$は役に立たないから」
虚数は、歴史的には3次方程式の解の公式と関わりがあるそうです:
虚数は、必要ない・意味のない数として考えられていました。例えば、$${x^2+1=0}$$ は「解なし」と考えられていました。
しかし、3次方程式の解の公式を考えるためには虚数が必要になったそうです。
詳しくは、以下の記事で書かれていて、参考になると思います。
また、複素数平面・複素関数論・代数学の基本定理など
色々な数学の分野で、複素数が使われています。
だったら、1÷0 もみんなが気づいていないだけで、本当は役に立つのではないか?
じゃあ、1÷0 を考察してみよう、というのがこの記事の目的です。
まずは虚数をおさらい
虚数や複素数について、よく理解している人は、ここは読み飛ばしても大丈夫です。
虚数は、記号 $${i}$$ を使います。(imaginary number の頭文字)
その定義は、
$${x^2=-1}$$
を満たす解
として定義します。(厳密には、2次方程式の解は2つあるので、解の一方を選ぶことになります。)
さらに、虚数の発展として、複素数を次で定義します。
複素数 $${\alpha}$$ とは、実数 $${a, b}$$ を用いて
$${\alpha = a+bi}$$
と書ける数のことを言う。
虚数や複素数が役立つ理由として、色々な”良い”性質を持っているからです。ここでは、いくつか紹介していきます。
足し算や掛け算が自然に定義出来る。つまり、
$$
(a+bi)+(c+di)=(a+c)+(b+d)i \\
(a+bi)\times(c+di)=(ac-bd)+(ad+bc)i
$$
が成り立つ。しかも、実数の足し算や掛け算と同じように良い性質を持っています。以下では、複素数を $${\alpha, \beta, \gamma}$$ とします。
(結合法則:足し算や掛け算は順番に依らない)
$$
(\alpha+\beta)+\gamma=\alpha+(\beta+\gamma), \\
(\alpha \times \beta)\times \gamma=\alpha \times (\beta \times \gamma).
$$
(分配法則)
$$
(\alpha +\beta)\times \gamma =(\alpha \times \gamma) + (\beta \times \gamma).
$$
これらの性質は、当たり前のように教科書に書かれています。ここでは、深入りしませんが、上記の性質が成り立つのは、「都合のいい・特別な場合」に限られます。
1÷0とは何か?
まずは割り算の復習
割り算とは、掛け算の”逆の演算”として定義します。つまり、
$$
a\div b=c \Leftrightarrow a=b\times c
$$
が成り立つことが、割り算の定義です。
簡単な例として、$${\frac{1}{3}}$$ を見てみましょう。
以下の図のように、$${\frac{1}{3}}$$ は、"1を三等分した数"です。
これは、裏を返せば、$${\frac{1}{3}}$$ が3つ集まると、1 になります。
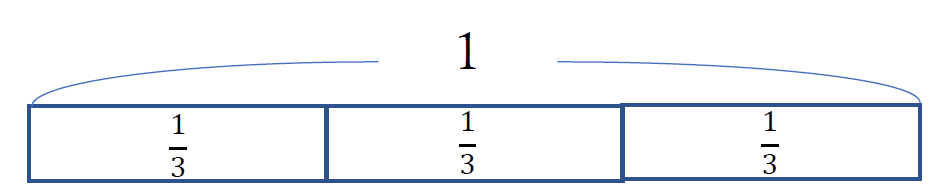
これが、「割り算が掛け算の逆の演算である」という意味です。
0で割る?
上の割り算の定義のもと、”0で割る”ことを考えてみましょう。
試しに、$${z=1\div 0}$$ と置いてみましょう。すると、割り算の定義より、
$$
z=1\div 0 \Leftrightarrow z\times 0=1
$$
が成り立つことになります。
しかし、どんな数(実数や複素数)に0をかけても、その結果は0になります。したがって、$${z=1\div 0}$$ という数は存在しない、つまり、定義できないのです。
ですが、虚数の時と同様に、$${\frac{1}{0}}$$ という数を定義してみたらどうなるのでしょうか?
和や積は都合が悪い
1÷0を定義しない一番の理由は、
和や積が”良い”性質を持たないから
ではないか、と私は考えています。
実際にいくつかの計算を調べてみましょう。
ここでは、1÷0を次のように定義して考えます:
$${z=1\div 0}$$ を
$$
z\times 0=1
$$
を満たす数として定義する。
注)数学の世界で、”定義することは自由”です。しかし、その定義が「良い性質を持つ」・「矛盾がない定義である」必要があります。
まずは、次の計算をしてみましょう。
$$
(z\times 0) \times 0 =1\times 0=0.\\
z\times (0 \times 0)=z \times 0=1.
$$
当然、上の2つの式は同じ値ではありません。
つまり、掛け算の順番に依ってしまいます。(結合法則が成立しない)
もう一つ、計算を見てみましょう。
$$
z\times (0+0)=z\times 0=1.\\
z\times 0+z\times 0=1+1=2.
$$
こちらも、分配法則が、1÷0 を定義すると成り立ちません。
上の2つの計算の通り、複素数では成り立つ"良い"性質が、1÷0 では成り立ちません。
これが、1÷0 を定義しない理由の一つです。
注)抽象的な話~環論や輪論~
大学の数学科では、環論を学びます。
環とは、ざっくり言うと、足し算と引き算、掛け算を一般化した概念です。
例えば、結合則や分配法則は、環の世界でも成り立ちます。
この抽象的な環論では、実数と同じく $${a\times 0=0}$$ が成り立ちます。つまり、0 で割ることができないのです。
厳密な定義はしませんが、こんな感じです:
$$
a\times 0=a\times (0+0)=a\times 0 +a\times 0.\\
両辺から, a\times 0 を引くと, \\
a\times 0 -a\times 0=a\times 0 +a\times 0 -a\times 0.\\
0=a\times 0.
$$
一方で、輪論といって、0で割ることを許す理論もあるみたいです。
こちらでは、結合則や分配法則のようなきれいな法則は成立しません。
まとめと次回予告
今回、「なぜ虚数は定義するのに、1÷0 は定義しないのか?」という疑問を考えてみました。
その理由として、和や積に関して、良い性質が成り立たないことを考察しました。これでは、複素数と同じように考えることは難しそうです。
しかし、ここで終わっていいのでしょうか?
もしかしたら、1÷0 が良い性質を持つかもしれない。
もしかしたら、1÷0 は役に立つかもしれない。
もしかしたら、まだ誰も気づいていないだけかもしれない。
次回は、もっと踏み込んで、「実際に定義したらどうか?」を考えていきます。(予定)
参考文献
[数学小話] 「数の歴史3 虚数の誕生まで」
1÷0 に関して、いくつか yahoo 知恵袋で質問があったので紹介します。
Yahoo 知恵袋
この記事が参加している募集
この記事が気に入ったらサポートをしてみませんか?
