確率・統計

2022年2月28日 22:30

文体が変わったらChatGPT4くんがまぎれこんでます。

参考図書
続・わかりやすいパターン認識―教師なし学習入門― 単行本（ソフトカバー） – 2014/8/26 石井健一郎 (著), 上田修功 (著)
パターン認識と機械学習上単行本（ソフトカバー） – 2012/4/5
C.M. ビショップ (著), 元田浩 (監訳), 栗田多喜夫 (監訳), 樋口知之 (監訳), & 2 その他
確率論の基礎概念 (ちくま学芸文庫) 文庫 – 2010/7/7
A. N. コルモゴロフ (著), 坂本實 (翻訳)

なにやっとるべや？

まず集合論で記述される。
集合論は集合同士の演算を記述し、その集合の要素は数である必要すらない。また、確率論の導入においては集合の要素は根源事象や事象であって数ではない。
$${\Omega}$$ : 標本空間。全体集合。必用な要素を全部ならべる。これの要素は確率論の導入においては根源事象であって数ではない。根源事象については用語の項を参照。
$${F}$$ : 集合族。集合の集合。ここで集合同士の演算に関するルールを満たす集合を集める。集合を集めた集合を作る。確率論においては個々の集合を事象という。
確率論においては、この族はボレル集合族である。

ボレル集合族は実数上に構成される完全加法族の最小構成である。
完全加法族は
・空集合を族に含む。
・ある集合の、全体集合における補集合も族に含む。
・集合同士を無限に和をとったとしても、その和集合も族に含む。この時の和が有限の和だと有限加法族である。

完全加法族は無限和についてしか規定しないが、ドモルガンの法則により無限の交差についても自動的に閉じる。

$${\Omega, F}$$の組を可測空間という。この空間には安心して測度を定義できる。

$${\mu}$$ : 測度。完全加法族上に定義される。完全加法族Fの要素（集合、確率論だと事象）を入力とし、非負の実数を出力とする関数。また以下の条件も満たす必要がある。
・入力に空集合をとると出力は０
・互いに共通部分を持たない（互いに素、あるいは排反）な集合の和集合を入力にとると、出力はここの集合の出力の総和。

特に確率測度$${P}$$を定め、この出力の範囲は０から１とする。（入力に空集合をとると出力は０、空集合の補集合である全体集合を入力にとると出力は１）

・さらに加えて（これを拡張して）、確率測度$${P}$$の極限を考えることができる。
（入力の集合から要素を抜き出していき、やがてそれらの積集合が空集合に至る場合、そうなった時の集合に対する測度の出力も０であること（コルモゴロフp37））

ここまでで$${(\Omega, F, P)}$$の組を確率空間といい、Fがボレル集合族ならばボレル確率空間という。

ここで$${\Omega}$$の要素である根源事象を入力にとり、実数を出力にとる関数を確率変数と呼ぶ。確率変数は、根源事象を実数空間に１対１、１対多、多対１でマッピングする。
最初に根源事象の集合に対してボレル集合族を作成したが、確率変数によって実数空間上にもボレル集合族が形成される。
測度は、入力が集合から実数にごそっと入れ替わるが、出力は相変わらず０から１の実数（確率）となる。
この時、確率変数の出力である実数領域を入力にとり、確率を出力する関数を確率分布という。確率分布は実数上のボレル集合族上に定義されるから測度である。確率分布は確率測度の特殊形とみなせる。
（確率分布は正確には確率変数の出力である実数空間から標本空間$${\Omega}$$上に形成されるボレル集合族の要素への逆写像によって定義される。コルモゴロフp49）

ここまですると、我々は確率を安心して足したり引いたり、掛けたり割ったり、微分したり積分したりすることができるようになる。

用語

試行(trial)：『コインを投げる』『コインを２回投げる』『サイコロを振る』『サイコロを２個投げる』など
ω：根源事象(fundamental event)：コインの表、裏、サイコロの出目。試行の結果起こりえる個々の結果。
Ａ：事象：確率事象。試行の結果起こり得ること、根源事象の組み合わせ。根源事象の集合。『１の目が出る』『５以下の目が出る』『偶数の目がでる』など。
Ｆ：事象の集合。集合の集合＝集合族。確率論の文脈では集合体（有限加法族）である。また、より一般的にはσ集合体（σ代数、完全加法族）が用いられる。また、そこから具体的に応用するためにボレル集合体を用いることもある。事象を扱ってる時は集合体やσ集合体。確率変数を扱いだすとボレル集合体になる。コルモゴロフはσ集合体＝ボレル集合体としている(p41)
Ω：全事象(whole event)あるいは標本空間(sample space)：根源事象全部。事象は全事象の部分集合となる。また、集合論的には全体集合(universal set)
Ｐ：確率測度(Probability Measure)：事象を非負の実数と対応付けるもの。事象の集合を扱うもの。確率分布とは塩梅がことなる。

基本的にある集合（Ω：全事象）の部分集合（Ａ：事象）は、大元の集合の要素（ω：根源事象）の組み合わせによって膨大に生成されるため、部分集合（Ａ：事象）を全部集めた集合（Ｆ）の要素の総数は最初の集合（Ω：全事象）の要素の総数より多くなる。

1. 全事象（根源事象の集合）Ωの要素数： $${ |Ω| = n }$$
2. 事象A（Ωの部分集合）の総数（空集合と全体集合を含む）： $${ |F| = 2^n }$$
3. ある事象Aの要素数： $${ |A| \leq |Ω| = n }$$

ある要素が存在するしないで２パターン。要素がn個なら、
２×２×２×２×...で２のn乗になる。

具体例

試行『コインを投げる』に対して、起こり得る根源事象は
ω={表},{裏}
事象は
A=『表』『裏』
全事象は
Ω={{表},{裏}}あるいは表記だけ変えて{表,裏}

試行『コインを２回投げる』に対して、起こり得る根源事象は
ω={表表},{表裏},{裏表},{裏裏}
事象は
A=『両方表』『両方裏』『少なくとも１枚が表』など
その組み合わせは前述の通り、根源事象の総数４個とみて、その根源事象各々が有る/無いの２パターンであるからして、２パターンの総個数乗
4C0+4C1+4C2+4C3+4C4=16パターン=2^4
全事象は
Ω={{表表},{表裏},{裏表},{裏裏}}あるいは表記だけ変えて{表表,表裏,裏表,裏裏}

コインを2回投げると根源事象の総数n=4

$$
\Omega = (w_1, w_2, …, w_n)
$$

であって、w_1={表表}, w_2{表裏}, w_3{裏表}, w_4{裏裏}

そもそもコインの場合は、表裏の2値であるから、
根源事象の総数が2^{投げた回数}になる。
コインを2回投げたのであれば総数n=2^2
事象の総数はその組み合わせの総和16パターン。

試行『サイコロ振る』に対して、起こり得る根源事象は
ω={1}, {2}, {3}, {4}, {5}, {6}
事象は
A=『奇数の出目』『偶数の出目』など
全事象は
Ω={1,2,3,4,5,6}

事象Ａの起こり得る確率は
P(A)=事象Ａに含まれる根源事象の数/根源事象の総数

適当に疑似コード書くと

double P(Event[] elementaryEvents)
{
	int count = 0;
	for(int i = 0; i<elementaryEvents.count; i++)
	{
		if(Satisfy(elementaryEvents[i]))
		{
			count++;
		}
	}
	return (double)count/(double)elementaryEvents.count;
}

余事象

ある事象Aに対して、事象Aじゃない方。補集合。
余事象をA^cとすると

$$
A \cup A^c = \Omega
$$

$$
A \cap A^c = \emptyset
$$

$${\emptyset}$$は空事象、空集合。

U（カップ）は和事象、和集合。or。union。あるいは。または。どちらか一方でも真ならば真。少なくとも一方が真ならば真。

Uの逆のやつは（キャップ）は積事象、積集合。and。intersection。かつ。どちらも真ならば真。また、確率に適用された場合は同時確率も示す。

また空集合の補集合は全体集合。

$$
\emptyset^c=\Omega
$$

確率の公理

コルモゴロフ

世の事象現象と数字を結びつけることで世の事象現象を数学的に扱えるようにする。すなわち足し算掛け算、微分積分が使えるようにする。

確率論の基礎概念 (ちくま学芸文庫) 文庫 – 2010/7/7
A. N. コルモゴロフ (著), 坂本實 (翻訳)

・(1) Ｆは集合体である。
・(2) Ｆの各集合Ａに非負の実数Ｐ（Ａ）が定められている。この非負の実数Ｐ（Ａ）を事象Ａの確率という。
・(3) Ｐ（Ω）＝１
・(4) ＡとＢとが共通の要素を持たない時Ｐ（Ａ＋Ｂ）＝Ｐ（Ａ）＋Ｐ（Ｂ）

この公理を満たす３つの組（Ω,Ｆ,Ｐ）を広義の確率空間という。
p37より、連続性の公理(5)を加える。

また、Ｆは集合体。（集合$${\Omega}$$の族$${F}$$について、$${\Omega \in F}$$であり、族$${F}$$に含まれる集合の和・差・積の結果もまた族$${F}$$に含まれる時、$${F}$$を集合体という）

p37
$${F}$$が加算個（無限個）の集合の和について閉じていると、σ集合体とみなされる。
p41
特に$${F}$$がボレル集合体ならば、（Ω,Ｆ,Ｐ）はボレル確率空間という。

Ｐは確率測度。

・(5) Fの事象の減少列$${A_1 \supseteq A_2 \supseteq … \supseteq A_n \supseteq …}$$について$${\bigcap\limits_nA_n=\emptyset}$$ならば$${\lim\limits_n P(A_n)=0}$$

この公理(5)によって集合体(有限加法族)のFはσ集合体(σ代数、完全加法族)に拡張される。

エクセンダール

確率微分方程式単行本（ソフトカバー） – 2012/4/5
B.エクセンダール (著)

Fがσ集合体であるからには以下が満たされる

空集合はFに含まれる：$${\emptyset \in \mathcal{F}}$$
集合AがFに含まれるならば、その補集合も含まれる：$${A \in \mathcal{F} \Rightarrow A^{c} \in \mathcal{F}, \quad A^c=\Omega/A}$$
集合A1, A2, ..., An, ...がFに含まれるならば、その無限個の和集合もFに含まれる：$${A_{1}, A_{2}, ..., A_{n}, ... \in \mathcal{F} \Rightarrow \bigcup_{i=1}^{\infty} A_{i} \in \mathcal{F}}$$

$${(\Omega, \mathcal{F})}$$を可測空間。
ここで$${P: \mathcal{F}\rightarrow [0,1]}$$かつ

$$
P(\emptyset)=0, P(\Omega)=1\\
A_1,A_2…\in\mathcal{F}\text{かつ}\lbrace A_i \rbrace \text{が互いに素}( A_i \bigcap A_j=0, i \neq j)\text{ならば}
P(\bigcup\limits_{i=1}^\infty A_i)=\sum\limits_{i=1}^\infty P(A_i)
$$

の時、$${(\Omega, \mathcal{F}, P)}$$を確率空間。
また、Ｆはσ集合体。Ｐは確率測度(p8)。

任意の集合族に対し、それを含む最小のσ集合体が存在する。
集合族が位相空間の開集合全体の時、σ集合体はボレル集合体。

有限加法族（finitely additive class）

集合体(field of sets)
集合代数（algebra of sets, algebra over a set）

Ｆが集合体であるとは、Ｆの要素である集合（事象）同士の和・差・積をとった集合もまたＦの要素であるようなＦ。サイコロの出目の話をしている時に『７』とか『１．２』とかが混ざってこないようなＦ。

有限加法族や完全加法族は元々和集合（ユニオン）と補集合（補）に対して閉じているという条件がありますが、それらの操作とド・モルガンの法則を組み合わせることで、実質的に積集合（インターセクション）に対しても閉じていることが求められます。

ド・モルガンの法則

$$
(A \cup B)^c = A^c \cap B^c \\
(A \cap B)^c = A^c \cup B^c
$$

ただし、無限個の交差についての閉性は持たないことに注意してください。

有限加法族とは、次の条件を満たす集合族のことを指します：

空集合は有限加法族に含まれる：$${\emptyset \in \mathcal{A}}$$
集合Aが有限加法族に含まれるならば、その補集合も含まれる：$${A \in \mathcal{A} \Rightarrow A^{c} \in \mathcal{A}}$$
集合A1, A2, ..., Anが有限加法族に含まれるならば、その和集合も含まれる：$${A_{1}, A_{2}, ..., A_{n} \in \mathcal{A} \Rightarrow \bigcup_{i=1}^{n} A_{i} \in \mathcal{A}}$$

ただし、無限の和について閉じているとは限らない。
また、空集合を含み、かつその補集合も含むので、自動的に全体集合を含む。

完全加法族（completely additive class）

σ-代数（σ-algebra）
σ-集合体（σ-field）
σ-加法族
σ-集合代数（σ-algebra [of subsets over a set]）
可算加法族（countably additive class）

空集合は完全加法族に含まれる：$${\emptyset \in \mathcal{F}}$$
集合Aが完全加法族に含まれるならば、その補集合も含まれる：$${A \in \mathcal{F} \Rightarrow A^{c} \in \mathcal{F}}$$
集合A1, A2, ..., An, ...が完全加法族に含まれるならば、その和集合も含まれる：$${A_{1}, A_{2}, ..., A_{n}, ... \in \mathcal{F} \Rightarrow \bigcup_{i=1}^{\infty} A_{i} \in \mathcal{F}}$$

有限加法族と異なり、
任意の可算個（つまり、無限個でもよい）の集合の和集合をとれる。閉じている。
また、空集合を含み、かつその補集合も含むので、自動的に全体集合を含む。

完全加法族じゃない例

$${\Omega\lbrace 1,2,3,4,5,6\rbrace}$$の時、$${F\lbrace \lbrace 1\rbrace\rbrace}$$のみとると$${\lbrace 1\rbrace}$$の補集合の$${\lbrace 2,3,4,5,6\rbrace}$$が$${F}$$に含まれていないため、$${F}$$はσ加法族ではない。そもそも$${\Omega\lbrace 1,2,3,4,5,6\rbrace}$$が含まれていないし、その補集合$${\emptyset}$$も含まれていない。

$${F\lbrace \lbrace 1\rbrace, \lbrace 2\rbrace\rbrace}$$などととってみると、和集合$${\lbrace 1,2\rbrace}$$が$${F}$$に含まれていないため、$${F}$$はσ加法族ではない。そもそも$${\lbrace 1\rbrace}$$および$${\lbrace 2\rbrace}$$らの補集合である$${\lbrace 2,3,4,5,6 \rbrace}$$および$${\lbrace 1,3,4,5,6\rbrace}$$も$${F}$$に含まれていないし、$${\Omega\lbrace 1,2,3,4,5,6\rbrace}$$も、その補集合である空集合$${\emptyset}$$も$${F}$$に含まれてない。

最低限度のσ加法族は$${\lbrace \emptyset,\Omega \rbrace}$$
最大は$${\Omega}$$のべき集合

ちな、$${\lbrace \emptyset\rbrace}$$と表記すると集合の集合になる。

最小の完全加法族に一個要素（集合）を足す。

ChatGPT4より

最小のシグマ加法族 $${\emptyset, \Omega}$$ に新しい要素 A を追加しましょう。ここで A は $${\Omega}$$の部分集合であるとします。A を含めた集合族がシグマ加法族であるためには、上記で述べた3つの条件を満たす必要があります。

空集合が含まれる: この条件は最初から満たされています。
補集合の閉性: A が新しい集合族に含まれるため、その補集合 $${A^c}$$ も含まれる必要があります。$${A^c}$$ は $${\Omega}$$ から A を取り除いた集合で、$${\Omega}$$の部分集合です。
加算個な和集合の閉性: この集合族に含まれる集合の有限または可算無限の列の和集合が含まれる必要があります。すなわち、$${\emptyset, A, A^c, \Omega}$$の組み合わせです。

$$
A_0=\lbrace \rbrace \\
A_1=\lbrace \emptyset \rbrace \\
A_2=\lbrace A \rbrace \\
A_3=\lbrace A^c \rbrace \\
A_4=\lbrace \Omega \rbrace \\
A_5=\lbrace \emptyset, A \rbrace \\
A_6=\lbrace \emptyset, A^c \rbrace \\
A_7=\lbrace \emptyset, \Omega \rbrace \\
A_8=\lbrace A, A^c \rbrace \\
A_9=\lbrace A, \Omega \rbrace \\
A_10=\lbrace A^c, \Omega \rbrace \\
A_11=\lbrace \emptyset, A, A^c \rbrace \\
A_12=\lbrace \emptyset, A, \Omega \rbrace \\
A_13=\lbrace \emptyset, A^c, \Omega \rbrace \\
A_14=\lbrace A, A^c, \Omega \rbrace \\
A_15=\lbrace \emptyset, A, A^c, \Omega \rbrace \\
$$

これらの和集合は、それぞれ $${\emptyset, A, A^c}$$ および $${\Omega}$$ であり、すでに集合族に含まれています。

例えば
$${\emptyset}$$と$${A}$$の和は$${A}$$であり、
$${\emptyset}$$と$${A^c}$$の和は$${A^c}$$です。
また、$${\emptyset}$$と$${\Omega}$$の和は$${\Omega}$$です。

$${A}$$と$${A^c}$$の和は$${\Omega}$$であり、
$${A}$$と$${\Omega}$$の和は$${\Omega}$$です。
また、$${A^c}$$と$${\Omega}$$の和は$${\Omega}$$です。

したがって、新しい要素 A とその補集合 $${A^c}$$ を含む集合族 $${\lbrace \emptyset, A, A^c, \Omega \rbrace}$$ は、シグマ加法族の条件を満たします。

ボレル集合

ボレル集合は、実数の集合の特殊な部分集合であり、測度論と確率論において特別な役割を果たします。これらの集合はエミール・ボレルの名前に由来し、彼の主要な業績を称えて名付けられました。

具体的には、ボレル集合は実数上の最小のσ-代数を形成する集合のことを指します。ここでσ-代数とは、空集合を含み、補集合と可算無限和（つまり、合併）に対して閉じている集合のことを指します。

実数上のボレル集合は以下の手順で構成できます。

開区間（すなわち、(a, b)の形のすべての集合）から始めます。
これらの開区間の補集合を取ります（これらは閉区間となります）。
これらの開区間と閉区間の可算個の合併と交差を取ります。このプロセスは無限に繰り返すことができます。

この結果得られる集合の集まりがボレル集合となります。

$$
\mathcal{B} = \sigma(\mathcal{O})
$$

ここで、$${O}$$は実数直線上の全ての開集合の集合を表し、$${σ(O)}$$はこれらの開集合に関して閉じた最小のσ-代数を表します。

確率空間

ある条件を満たす集合族である。標本空間$${Ω}$$、確率測度の定義された$${Ω}$$の部分集合の族$${F}$$（σ代数、σ集合体、すなわち完全加法族）、$${F}$$上の関数である確率測度$${P}$$からなる組

$${(\Omega, F, P)}$$

可測空間

集合$${\Omega}$$とその部分集合からなるσ加法族$${F}$$があるとき、その組$${(\Omega, F)}$$を可測空間という。

測度空間

可測空間に測度$${\mu}$$を追加すると測度空間となる。

$${(\Omega, F, \mu)}$$

測度は集合と実数を対応付ける関数。
また、無限を対応付けることも許される。
頭をからっぽにしたければ入力を集合、出力を実数および無限と考えて良く、特に出力の実数は非負であり、入力が空集合なら出力の実数は０である。

1.非負性: 任意の集合 A に対して、$${\mu(A) \geq 0}$$
2.空集合の測度: $${\mu(\emptyset) = 0}$$
3.可算加法性: 互いに排反な可算個の集合 $${A_1, A_2, A_3, \dots}$$ に対して、$${\mu\left(\bigcup_{n=1}^{\infty} A_n\right) = \sum_{n=1}^{\infty} \mu(A_n)}$$

完備

σ集合体$${F}$$と
測度Pがあって、

外測度$${P^*(G)=0}$$

$$
P^*(G) := \text{inf} \lbrace P(A); A\in F, G\subset A \rbrace =0
$$

を満たす集合$${G}$$が、全て$${F}$$に含まれる場合、
確率空間$${(\Omega, F, P)}$$は完備。

測度

ルベーグ測度は、集合の「大きさ」を一般化したもので、実数の部分集合やより一般的な空間上の集合について定義することができます。

区間というのは極めて単純な集合です。

区間: 一般に、実数の区間とは、ある2つの実数 $${a}$$ と $${b}$$ （$${a≤b}$$）に対して、$${a}$$ と $${b}$$ の間のすべての実数を含む集合を指します。つまり、$${I={x∈R∣a≤x≤b}}$$を区間と呼びます。また、これは閉区間とも呼ばれます。

閉区間: 閉区間とは、その端点を含む区間のことを指します。つまり、$${I=[a,b]={x∈R∣a≤x≤b}}$$を閉区間と呼びます。
開区間: 開区間とは、その端点を含まない区間のことを指します。つまり、$${I=(a,b)={x∈R∣a<x<b}}$$を開区間と呼びます。

例えば

閉区間 [a, b]:
1. 測度（ルベーグ測度）: $${m([a,b])=b−a}$$
2. 外測度（ルベーグ外測度）: $${m∗([a,b])=b−a}$$
半開区間 [a, b):
1. 測度（ルベーグ測度）: $${m([a,b))=b−a}$$
2. 外測度（ルベーグ外測度）: $${m∗([a,b))=b−a}$$
開区間 (a, b):
1. 測度（ルベーグ測度）: $${m((a,b))=b−a}$$
2. 外測度（ルベーグ外測度）: $${m∗((a,b))=b−a}$$

ルベーグ測度とルベーグ外測度が異なる結果を返す一例として、有理数の集合を考えることができます。

実数の間隔 [0,1] 内の有理数の集合を $${Q}$$ とします。有理数は実数全体の間隔内で稠密に存在しますが、その「量」（正確には「ルベーグ測度」）は実際には0となります。これは、任意の有理数の近くには必ず無理数が存在し、したがって有理数を「捉える」ための区間をどれだけ小さくしても、その和は必ず0になるからです。

したがって、この集合 $${Q}$$ のルベーグ測度は0です。

しかし、$${Q}$$ の外測度を考えると、外測度は「包む」最小の開集合の測度を考えます。この場合、$${Q}$$ を包む最小の開集合は間隔 [0,1][0,1] 自体となります（有理数は実数間隔内で稠密に存在するため）。そのため、$${Q}$$ の外測度は1となります。

これにより、同じ集合 $${Q}$$ についてルベーグ測度とルベーグ外測度が異なる結果を返すことが分かります。

有理数の集合は測度０

「点の集合」の観点から: 単一の点の集合（つまり、1つだけの要素からなる集合）を考えてみましょう。このような集合の「長さ」や「体積」はどれくらいになるでしょうか？直感的には、1つの点は「長さ」も「体積」も持たないため、その測度は0になります。そして、ルベーグ測度は「可算加法性」を持つので、点の集合がどれだけ多くても、それぞれの点の測度が0であるため、全体の測度も0になります。
「無限小の区間の和」の観点から: 同様に、無限小の区間（つまり、長さが0に近い区間）の無限個の集合を考えてみましょう。このような区間のそれぞれの「長さ」は0に近いため、その「長さ」の合計（つまり、その測度）も0になります。
「ほとんど至るところ」の観点から: 測度0の集合は、「ほとんど至るところ」でその性質が成り立つという概念と密接に関連しています。例えば、ルベーグ測度においては、測度0の集合の外側である「ほとんどすべて」の点について、ある性質が成り立つと言います。これは、測度0の集合が「無視できるほど小さい」ことを意味します。

外測度

外測度の概念を理解するための最も基本的な例を考えてみましょう。ここでは実数の部分集合に対するルベーグ外測度を考えます。

まず、最も単純な例としては、閉区間$${I=[a,b]}$$を考えてみましょう。この場合、この閉区間を完全に覆う最小の開区間は $${(a−ϵ,b+ϵ)}$$（ここで $${ϵ}$$ は任意の正の実数）です。したがって、この開区間の「長さ」、すなわち $${b−a+2ϵ}$$ を考えると、$${ϵ}$$ を0に近づける（つまり、下限を取る）ことで、閉区間$${I}$$ の外測度が $${b−a}$$ となることがわかります。つまり、この場合、閉区間の外測度はその「長さ」、すなわち端点間の距離と等しくなります。

次に、有限の個数の閉区間の和集合について考えてみましょう。すなわち、$${I_1=[a_1,b_1],I_2=[a_2,b_2],…,I_n=[a_n,b_n]}$$ という $${n}$$ 個の閉区間を考え、これらの和集合 $${E=I1∪I2∪…∪In}$$ を考えます。この場合、各閉区間を別々に覆う開区間を考え、それらの開区間の長さの和を考えることで、 $${E}$$ の外測度を計算することができます。具体的には、各閉区間 $${I_i}$$ の外測度は $${bi−ai}$$ であるため、 $${E}$$ の外測度は $${b_1−a_1+b_2−a_2+…+b_n−a_n}$$ となります。つまり、この場合、和集合の外測度は各部分の外測度の和となります。

これらの例から、外測度が「大きさ」を一般化した概念であることがわかります。また、外測度が可算和については必ずしも加法的ではない（つまり、和集合の外測度が部分の外測度の和と等しくなるとは限らない）という重要な性質も理解できます。これは、無限個の部分に分割した場合や、分割した部分が重なっている場合などに特に重要となります。

例えば[1, 10][8, 12]など、区間が重複する場合。

この場合、和集合は$${E=I1∪I2=[1,12]}$$となります。これを覆う最小の開区間は$${(1−ϵ,12+ϵ)}$$となります。したがって、この開区間の長さは$${12−1+2ϵ=11+2ϵ}$$となります。そして、$${ϵ}$$を0に近づけることで、$${E}$$の外測度は11となります。

この結果から、和集合の外測度は各部分の外測度の和（つまり、10−1+12−8=13）とは異なることがわかります。これは、外測度が重複部分を「二重に数える」ことなく、「大きさ」を計算するための手段であることを示しています。つまり、外測度は集合の「大きさ」を一般化した概念であり、通常の長さや体積とは異なる性質を持つことがわかります。

確率測度

確率測度Pが満たすべきは

非負性: すべてのボレル集合 Aに対して、$${P(A)≥0}$$
正規化: 全体集合 Ω に対して、$${P(Ω)=1}$$
可算加法性: すべての互いに排反なボレル集合 $${A_1,A_2,A_3,…}$$ に対して、以下が成り立つ：$${P\left(\bigcup_{i=1}^{\infty} E_i\right) = \sum_{i=1}^{\infty} P(E_i)}$$

ここでボレル集合とは、最小のσ加法族Fを構成する集合A。

$$
\begin{array}{ll} 1. & \forall A, P(A) \geq 0, \\ 2. & P(\Omega) = 1, \\ 3. & \forall A_1, A_2, A_3, \ldots \text{ are disjoint, } P\left(\bigcup_{i=1}^{\infty} A_i\right) = \sum_{i=1}^{\infty} P(A_i). \end{array}
$$

加法

事象の排反

互いに重複のない事象、同時には起こらない事象、一方が起こった時にもう一方が起こらないような事象を排反という。例えばコインの表裏は同時にでない、サイコロの目は同時にでない、という風に。

$$
A \cap B = \emptyset
$$

確率の公理

事象ごとに０以上1以下の実数をとり、起こりうる全部の事象を足したら1、起こりえない事象は0。事象が互いに排反なら単純に足してよい。排反でない場合は下記参照。
このように、事象を入力とし、実数を出力する関数P()を確率という。

例えば理想的なサイコロにおいて、各目の出る確率は1/6で互いに排反。異なる出目が同時に出ることはない。1/6を6つ足したら１。７の目が出る可能性は０。角が地面に突き刺さるとか、そういう事象も考慮しない。

$$
0\leq P(A) \leq 1
$$

$$
P(\Omega) = 1, P(\emptyset) = 0
$$

事象が排反な場合の確率、事象の和集合の確率

$$
P(A\cup B)=P(A)+P(B)
$$

$$
P(A_1\cup A_2 \cup A_3 \cup…)=P(A_1)+P(A_2)+P(A_3)+…
$$

加法定理

事象が排反でない場合の確率、事象の和集合の確率

$$
P(A\cup B)=P(A)+P(B)-P(A\cap B)
$$

右辺、Ｕの逆のヤツは同時確率を示す。

乗法

条件付き確率

ある事象Aが起こった後に、別の事象Bが起こる確率を条件付き確率といい、以下のようにあらわす。

$$
P(B|A)
$$

例えばトランプで、スペードのカードを引いた後に、それがエースである確率、など。

事象の独立

ある事象の結果がほかの事象の確率に影響を与える時、その事象は従属、あるいは独立していないという。
ある事象の結果がほかの事象に確率に影響を与えない場合、その事象は独立しているという。

例えばトランプで、スペードのカードを引いた後に、それがエースである確率は独立しているが、スペードだけエースが３枚あるようなトランプの場合、この事象は独立していない。

事象の独立条件。Bの確率にAが関与してないの式。

$$
P(B)=P(B|A)
$$

事象A,Bが互いに独立な場合の確率、事象の積集合の確率
これは同時確率P(A,B)

$$
P(A\cap B)=P(A)P(B)
$$

拡張すると以下となる。

$$
P(A_1 \cap A_2 \cap …\cap A_n)=P(A_1)P(A_2)\times…P(A_n)
$$

単純な場合。
Aが絵柄の種類
Bが数字

最も考えやすいように考えると
種類が4種でP(A)=1/4
数字が13種でP(B)=1/13
独立しているのはP(B)=P(B|A)である時である。

トランプの単純な1セット52枚は、
どの絵柄を引いても、その後数字を引く確率は変わらない
エースを引く確率(4/52)と
スペードを引いてから、それがエースである確率はどちらも1/13
P(B|A) = P(エース|スペード)は、
P(エース)=P(エース|スペード)であってどちらも1/13。よって独立。

ちな、この設定でスペードのエースを引く確率は同時確率
同時確率P(B, A) = P(エース, スペード)
P(B, A)=P(B)P(A)=P(エース)P(スペード)=1/13*1/4=1/52

独立してない場合。例えばスペードを何枚かセットに追加した場合、種類の確率も偏るし数字の確率も偏る。

仮にスペードのエースを1枚追加した場合、問題はまだ容易い。
スペードのエースを引く確率は14/53*2/14=2/53
ただし、これは独立していない。

エースを引く確率は5/53
P(B)=P(エース)=5/53
スペードを引いてからエースを引く確率は
P(B|A) = P(エース|スペード)=2/14
これは独立していない。

同時確率P(B,A)=P(B,A)=P(スペード, エース)
=P(A)P(B|A)=P(スペード)P(エース|スペード)=14/53*2/14 独立じゃない
=P(B)P(A|B)=P(エース)P(スペード|エース)=5/53*2/5 独立じゃない

乗法定理

事象A,Bが互いに独立じゃない場合の確率、事象の積集合の確率

$$
P(A\cap B)=P(A)P(B|A)=P(B)P(A|B)
$$

左辺、Ｕの逆のやつは同時確率を示す。

$$
P(A, B)=P(B|A)P(A)
$$

この形はベイズの定理の分子でもでてくるし、
機械学習でもよくでる。

また、拡張すると以下である。
繰り返すが、事象が独立ではない場合に成り立つ。

$$
P(A_1 \cap A_2)=P(A_1)P(A_2|A_1)\\
P(A_1 \cap A_2 \cap A_3)=P(A_1 \cap A_2)P(A_3|A_1\cap A_2)=P(A_1)P(A_2|A_1)P(A_3|A_1\cap A_2)\\
P(A_1\cap A_2 \cap … \cap A_n)=P(A_1)P(A_2|A_1)P(A_3|A_1\cap A_2)\times …P(A_n|A_1\cap …\cap A_{n-1})
$$

また同時確率でも同じように以下。
繰り返すが、事象が独立ではない場合に成り立つ。

$$
P(A_1, A_2)=P(A_1)P(A_2|A_1)\\
P(A_1, A_2, A_3)=P(A_1, A_2)P(A_3|A_1, A_2)=P(A_1)P(A_2|A_1)P(A_3|A_1, A_2)\\
P(A_1, A_2, … ,A_n)=P(A_1)P(A_2|A_1)P(A_3|A_1, A_2)\times …P(A_n|A_1, …,A_{n-1})
$$

ここまでまとめ

排反：同時に起こる起こらないの話。確率の和になる。
独立：原因と結果、因果関係の話。確率の積になる。

排反な場合

排反じゃない場合

独立な場合

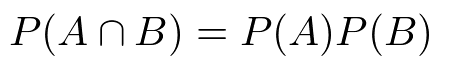
独立じゃない場合

Ｘ：確率変数(random variables)

根源事象と数字、とりわけ実数を対応付けるもの。事象を入力し、実数を出力する関数。例えばコインの表裏（事象）に0と1を対応付けるなど。この時、事象に対応付けられた出力の実数を実現値（0と1）という。すなわち、確率変数は入力が事象で、出力が実現値（実数）。

サイコロなどは出目がそのまま数字なので、そのまま分かり易く対応付けることができる。
コインやサイコロは離散型（出目が離散的）であるが、例えば時計の秒針の角度は連続型である。

離散型確率変数：確率変数の出力・出目が離散的（コイン、サイコロ）
連続型確率変数：確率変数の出力が連続的（時計の秒針の角度、デジタル化する前のアナログセンサーの入力（温度、湿度、圧力、音、光））

また、確率変数は必ずしも単一の事象に対して一つの数値を割り当てるとは限らず、複数の事象に対して一つの数値を割り当てることもありえる。例えば、サイコロを2回投げて得られる合計点数などがそれに当たる。

P(X):確率分布

確率分布(probability distribution)、確率関数(probability function)

確率変数X（の出力である実数）と、
確率0≦p≦1を対応させるP(X)のP()の部分。
あるいは（Ω,Ｆ,Ｐ）におけるＰ。

確率分布は確率変数を入力にとるわけではない。
確率分布が入力にとるのはあくまで、確率変数が取りうる各実現値（実数）である。

確率変数は、入力が事象で出力が実数値（実数）。
確率分布は、入力が実数値で、出力が確率。
確率分布は、確率変数が、その出力である実数値をとる確率を出力する。

累積分布関数(cumulative distribution function)のことを分布関数という場合もある。確率分布と分布関数は別の言葉。
確率質量関数(probability mass function)のことを確率関数という場合もある。確率関数という語は確率分布の場合もあれば確率質量関数の場合もある。
また、下図の$${f(x_i)=P(X=x_i)}$$のf(x)の部分をXの確率関数といい、確率と対応付いた$${f(x_i)=P_i}$$をXの確率分布というなど、微妙に使い分ける人もいる。

確率は関数として、事象を入力にとることもある。その場合P(A)。出力は0-1実数。
確率変数は事象入力実数出力。X(A)。出力の範囲は何でもいいが、出力の個数は有限個か無限個かで以降の扱いに差が出る。
確率分布は確率変数の出力である実現値入力の確率出力P(X)。あるいはP(X(A))。

$$
P(X=x)
$$

と書いた時、
大文字$${X}$$は確率変数で、
小文字$${x}$$は確率変数の実現値。
つまりこの表記の時点で、事象は関係ない。

$$
X=x_i
$$

のように、実現値にインデックスが付いてたら基本的には離散値出力の確率変数である。

$$
a \lt X \lt b
$$

のように、比較演算子で範囲指定してたら連続値出力の確率変数とみて良い。

総じて、大体以下のように表記されたりされなかったりする可能性がある。

$$
f(x_i)=P(X=x_i)
$$

実現値の捕捉

実現値に関する説明は本当に適当で、事象の様に扱っていたり、確率変数の入力のように扱うテキストが山ほどある。
P()が事象を入力に受けていたらそれは確率測度であって確率分布ではない。
分かりやすさのために($${X=事象}$$)みたいにして逆に良く分からない説明が試みられていることもある。

確率質量関数(probability mass function)、確率関数、重み関数

確率変数が離散値を出力する場合の確率分布$${p(x)}$$

確率密度関数(probability density function)

確率変数の出力が連続値の場合の確率分布$${p(x)}$$。確率変数の出力の個数が無限である場合、確率変数が唯一の値をとる確率は1/∞となり常に０となる。そのため確率変数の出力が区間a-bの間に入る確率と見て

$$
P(a\leq X\leq b)=\int_a^b p(x) dx
$$

のように扱う。ここでは確率変数を入力するP(X)、および右辺積分式の出力が確率。p(x)の出力が確率密度。p(x)自体あるいはp()が確率密度関数。
すなわち密度関数の出力である密度の積分をとると区間に入る確率がでる。

$$
p(x\in(a,b))=\int_a^b p(x) dx
$$

のように表記されることもある。

密度関数の規格化条件(normalization condition)

$$
\int_{-\infty}^{+\infty} p(x) dx=1
$$

密度関数の規格化定数(normalization constant)

密度関数がある関数$${q(x)}$$を用いて$${p(x)=const \times q(x) \quad (-\infty < x < +\infty)}$$で表される時の

$$
const=\int_{-\infty}^{+\infty} q(x) dx
$$

のことを規格化定数という。
この定数により密度関数は

$$
f(x)=\frac{q(x)}{const}=\frac{q(x)}{\int_{-\infty}^{+\infty} q(x) dx} \quad(-\infty < x < +\infty)
$$

で表される。この規格化定数により、密度関数は規格化条件を満たす。

累積分布関数(cumulative distribution function)、累積確率分布、分布関数

0-1の確率を足していくもの。この関数は単調に増加する右肩上がりの関数となる。確率変数が離散型でも連続型でも適用される。

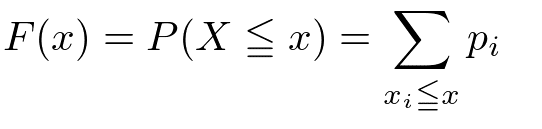
x以下のx_iについて全部足す。

xまで全部足す。

確率密度関数と累積分布関数の関係は

$$
F(b)-F(a)=P(a \leqq X \leqq b)=\int_a^bp(x)dx
$$

$$
p(x)=\frac{dF(x)}{dx}
$$

ここに至るに、確率において足し算掛け算微分積分が使えるようになった。

P(X,Y):同時確率（結合確率）

積集合$${P(X \cap Y)}$$でもある。

確率変数が複数。多変数関数に相当。
行と列をとって、交差するセルの一つの確率。
周辺確率は行の全部の確率、列の全部の確率。

$$
P(X,Y)
$$

確率変数が離散型の場合

$$
P(X=x_i, Y=y_j)=p_{ij} \quad (i=1…m, j=1…n)
$$

などと表現する。

周辺確率

インデックスをかたっぽ固定してもうかたっぽを走査したやつ。
また、これも加法定理という。

$$
P(X)=\sum \limits_Y P(Y,X), \quad P(Y)=\sum \limits_X P(X,Y)
$$

出力が連続値だと

$$
P(X)=\int_Y P(Y,X)dY
$$

あるいは乗法定理より
$${P(Y,X)=P(X,Y)=P(Y|X)P(X)}=P(X|Y)P(Y)$$だから

$$
P(X)=\sum \limits_Y P(Y,X)=\sum \limits_Y P(Y|X)P(X)=\sum \limits_Y P(X|Y)P(Y)
$$

あるいは表記を変えて

$$
p_{i\cdot}=\sum\limits_{j=1}^n p_{ij}, \quad p_{\cdot j}=\sum\limits_{i=1}^m p_{ij}
$$

iの横のドット、jの横のドットはあったりなかったりする。
または

$$
P(X=x_i)=\sum\limits_{j=1}^n P(X=x_i,Y=y_j)
$$

などと表現される。言ってることは全部同じである。

Xがm個、Yがn個の離散値をとるなら
m×n個の確率が生成されて
それらのm×n個の確率を全部足すと１
Xの周辺確率が（n個の確率を全部足した）m個、
Yの周辺確率が（m個の確率を全部足した）n個生成される。
Xの周辺確率をm個全部足すとその確率は１（m×n個の確率を全部足したことになる。）
Yの周辺確率をn個全部足すとその確率は１（m×n個の確率を全部足したことになる。）

$$
\sum\limits_X\sum\limits_YP(X,Y)=1\\
\sum\limits_XP(X)=\sum\limits_YP(Y)=1
$$

あるいは

$$
\sum\limits_{i=1}^m \sum\limits_{j=1}^n p_{ij} = 1\\
\sum\limits_{j=1}^m p_{i\cdot}=1, \quad \sum\limits_{i=1}^n p_{\cdot j}=1
$$

同時確率と周辺確率

同時確率は以下を満たす（乗法定理）。

$$
P(X,Y)=P(Y,X)\\
P(X,Y)=P(X|Y)P(Y)=P(Y|X)P(X)
$$

ここでP(Y),P(X)は周辺確率。
X,Yが互いに独立ならば

$$
P(X|Y)=P(X) ,\quad P(Y|X)=P(Y)\\
P(X,Y)=P(X)P(Y)
$$

ここのセルの確率と周辺確率が一致するような時。

周辺確率密度

確率変数が連続値だと

$$
P(X)=\int_Y P(Y,X)dY=\int_Y P(X,Y)dY\\
P(Y)=\int_X P(Y,X)dX=\int_X P(X,Y)dX
$$

２変数だと

$$
P(a \leqq X \leqq b, c \leqq Y \leqq d)=\int_a^b\int_c^dp(x,y)dxdy
$$

のようになって確率密度関数と称する。

条件付き独立

X,YとSが独立な時

$$
P(X,Y|S)=P(X|Y,S)P(Y|S)=P(Y|X,S)P(X|S)
$$

かつX,Yが独立$${P(X|Y,S)=P(X|S), \quad P(Y|X,S)=P(Y|S)}$$ならば

$$
P(X,Y|S)=P(X|S)P(Y|S)
$$

ベイズの定理

代表値（要約統計量）

チェビシェフの不等式

チェビシェフの不等式（Chebyshev's inequality）は、確率論と統計学において広く利用される重要な不等式です。ある確率変数が平均値からどれだけ遠くに散らばりうるか、あるいは確率変数の値が平均値の周囲にどれだけ密集しているかといったことを示すのに用います。
確率変数 $${X}$$ の平均値を $${\mu}$$ 、標準偏差を $${\sigma}$$ とすると、チェビシェフの不等式は次のように表されます：

$$
P(|X - μ| ≥ kσ) ≤ 1/k²
$$

ここで $${k}$$ は任意の正の実数です。この不等式は、「確率変数 $${X}$$ の値が平均値 $${\mu}$$ から $${k}$$ 個の標準偏差 $${\sigma}$$ より遠くにある確率は、 $${1/k^2}$$ 以下である」ということを表しています。

例えば、 $${k=2}$$ のとき、確率変数の値が平均値から2個の標準偏差より遠くにある確率は、最大でも $${1/4}$$ 、つまり25%であることがチェビシェフの不等式により保証されます。

この不等式は任意の確率分布に対して成り立ちますが、具体的な分布の形状がわかっている場合（例えば、正規分布など）、より精密な結果を得るための他の不等式や法則（例えば、68-95-99.7ルールなど）が利用できます。

確率変数の標準化、規準化、正規化

Xの偏差をとり、標準偏差で除す。

この時

これは正規分布のパラメータで表すと

$$
Z=\frac{x-\mu}{\sigma}
$$

検定

母集団と標本

母集団（Population）とは、研究や調査の対象となる全体の集合を指します。例えば、ある国の全ての住民、ある会社の全従業員、ある製品の全生産数などが母集団となり得ます。統計学では、この母集団から得られるデータを「母数（population parameter）」と呼びます。母数には、母平均、母分散、母比率などがあります。

一方、標本（Sample）とは、母集団から選ばれた一部の集合を指します。全ての母集団を調査するのは時間やコストの観点から難しいことが多いため、母集団から一部のデータを選び出して調査や分析を行うことが一般的です。このように選ばれた一部のデータが標本です。標本から得られるデータを「標本統計量（sample statistics）」と呼びます。標本統計量には、標本平均、標本分散、標本比率などがあります。

母集団と標本の関係は、統計学における基本的な概念で、推測統計学において重要な役割を果たします。母集団から標本を選び出す（サンプリング）方法や、標本から母集団の特性を推測する方法（推定や検定）などが研究されています。

この記事が気に入ったらサポートをしてみませんか？