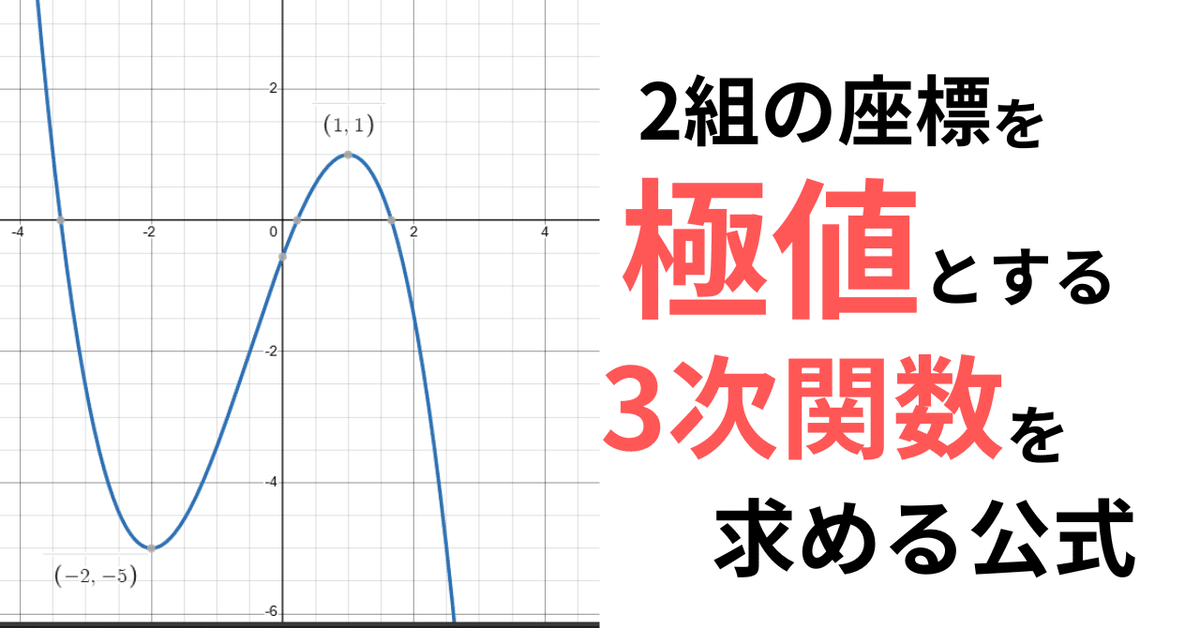
極値のx,yから3次関数の式を特定する

今回は$${x,y}$$の2組からその2組を極値とする3次関数の式を求める方法を解説します。問題を解くのには多分全く役に立ちませんが特定の値を答えとする問題作成をするときなどに有用です。

以前にも似たような記事(内容は違う)を出しているので良ければご覧ください。

極値を求める方法

まずは極値を求める方法をおさらいしておきましょう。

例題:$${f(x)=x^3-9x^2+15x+27}$$のとき、$${y=f(x)}$$の極値を求めよ。
①$${f'(x)}$$を求める
$${f'(x)=(x^3)'-9(x^2)'+15(x)'+(27)'}$$
$${=3x^2-18x+15}$$
②$${f'(x)=0}$$を解く
微分は接線の傾きを求めることなので、=0にすると接線の傾きなし、つまりx軸に平行ということになります。極値では必ず接線の傾きは0なので、これで極値のx値が求められます。
$${3x^2-18x+15=0}$$
$${3(x-1)(x-5)=0}$$
$${x=1,5}$$
③$${x}$$を$${f(x)}$$に代入して$${y}$$を求める
$${f(1)=1-9+15+27=34}$$
$${f(5)=125-225+75+27=2}$$
よって、$${x=1}$$のとき$${y=34}$$、$${x=5}$$のとき$${y=2}$$
④$${x^3}$$の係数から増減を推測して極大、極小の判断をする
今回は$${x^3}$$の係数は正の値なので増減は増→減→増のように変化する。よって、極大値はx=1のときy=34,極小値はx=5のときy=2

f'(x)からf(x)を求める

いきなり$${f(x)}$$を考えるのは難しいというか多分無理だと思うので極値を求めるときに使う$${f'(x)}$$から考えていきます。

まず、$${f(x)}$$の極値の座標を$${(p,m)(q,n)}$$とします。このとき、$${a}$$を定数として、$${f'(x)=3a(x-p)(x-q)}$$となります。($${3a}$$を掛けるのは$${f(x)}$$の$${x^3}$$の係数を$${a}$$だけにするため)。これを展開すると、$${f'(x)=3ax^2-3apx-3aqx+3apq}$$となり、$${\int f'(x)=f(x)}$$であるから$${f(x)=\int 3ax^2-3apx-3aqx+3apq  dx}$$となります。これを計算して整理すると、$${b}$$を積分定数として、$${f(x)=ax\{x^2-\frac{3}{2}(p+q)x+3pq\}+b}$$

a,bの値を連立方程式から求める

次に$${a,b}$$の値を求めていきます。まず、$${(p,m),(q,n)}$$はどちらも$${y=f(x)}$$上の点であることから、$${m=f(p),n=f(q)}$$が成り立ちますね。よって、次のような連立方程式が立てられます。

$$
\begin{cases}ap\{p^2-\frac{3}{2}(p+q)p+3pq\}+b=m\\aq\{q^2-\frac{3}{2}(p+q)q+3pq\}+b=n\end{cases}
$$

途中式は省略しますが、これを$${a,b}$$について解いて整理すると、

$$
a=\frac{2(n-m)}{(p-q)^3},b=\frac{mq^2(3p-q)+np^2(p-3q)}{(p-q)^3}
$$

となって、$${a,b}$$の値が求まります。

最終的な公式(?)

$$
2点(p,m),(q,n)を極値とする3次関数の式は、\\
a=\frac{2(n-m)}{(p-q)^3},b=\frac{mq^2(3p-q)+np^2(p-3q)}{(p-q)^3}とすると、\\
y=ax\{x^2-\frac{3}{2}(p+q)x+3pq\}+b
$$

公式の確認(関数描画ソフトを使用)

さて、公式を出したはいいものの、これが本当にちゃんと成立するのか直感的に納得できませんね。いちいち代入するのはさすがに大変なので、ここは文明の利器に頼りましょう。ここでは関数描画ソフトのDesmosを利用してやってみましょう。

Desmos | グラフ計算機

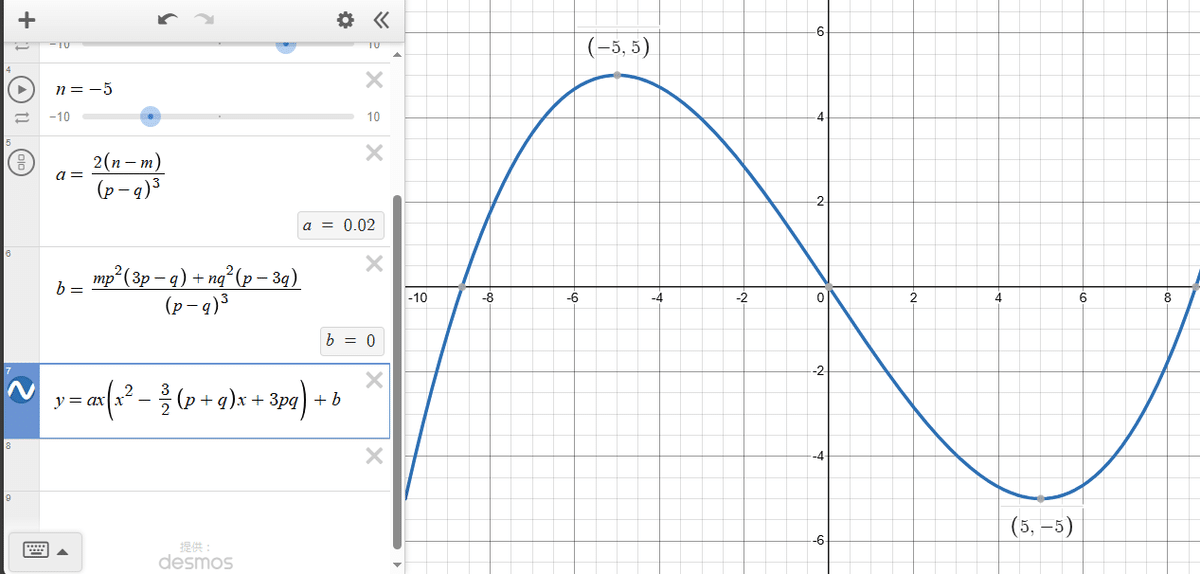
まずは下のように座標の値を入力する部分を作っておきます。ここでは(5,-5),(-5,5)にしていますが$${p\ne q,m\ne n}$$であれば*なんでも大丈夫です。また、入力すると下にスライダーが出てきますが気にする必要はありません。
*$${p=q}$$または$${m=n}$$だと極値が存在しないため。

次に、$${a,b}$$の値を指定します。公式をそのまま入力で大丈夫です。
入力すると下のようになります。右下の数値は気にしなくて大丈夫です。

最後に関数の式を入力しましょう。入力するとグラフができるはずです。

注：この画像ではbの値が間違った値になっています(この時点では気づいていない)
　1つ前か1つ後の画像が正しいものになっていますので入力時はそちらをご参照ください。

出てきたグラフをクリックすると極値や切片の位置に点がありますね。そこをクリックでその点の座標を見ることができます。極値がしっかり入力した値になっています。

ここで、入力しておいた$${p,q,m,n}$$の値をそれぞれ変えると、それに応じてグラフが変化するはずです。

今回紹介した公式は問題を解くのに役に立つものではないと思います。しかし問題を「作る」ときには、答えを狙った値にしたいときもあるかと思うので、これを使って作ってみてください！