2つの3次関数のグラフで囲まれた場所の面積を任意の値にする公式を作る(数学)

ふと積分を考えているときに面白そうだなと思って掘り下げてみたことですが、2つの関数グラフで囲まれた面積を自分で決めた値にすることってできるのかという疑問の解決について今回は書いていきます。

＊今回は3次関数同士での場合を考えますが、他の次数でも多分考え方は同じです。(ただし、交点は2個でないといけない)

2つの関数で囲まれた面積の求め方

3次関数を2つ作るとこのような感じで囲まれた面積ができたりします。ここを求める方法を考えていきます。

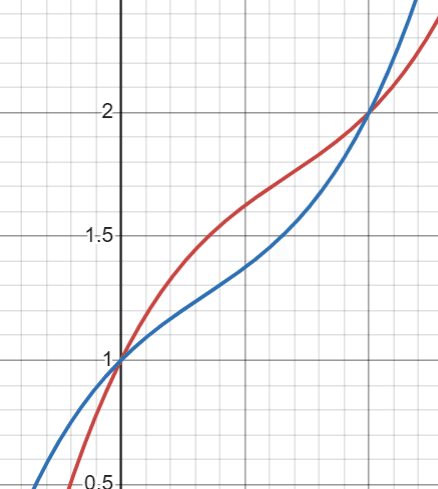
ここからは、囲まれているところでx軸から遠いほうのグラフ(ここでは赤)を$${f(x)}$$、近いほうのグラフ(ここでは青)を$${g(x)}$$として説明していきます。

①まずは2つのグラフの交点を求める
②$${f(x)}$$を交点1から交点2までで定積分する
③$${g(x)}$$を交点1から交点2までで定積分する
④②-③が囲まれた面積の値

この手順を1つずつ、そして任意の値にする公式の求め方も考えながら解説していきます。

2つのグラフの交点を求める

中学校で習うと思いますが、2つのグラフ$${y=f(x),y=g(x)}$$の交点を求めるには次のような連立方程式を解けば良いですね。これは1次関数に限らず、もっと次数が高くても成立します。

$$
\begin{cases} y=f(x)\\y=g(x)\end{cases}\\
つまり、f(x)=g(x)と変形できるので、\\
f(x)-g(x)=0をxについて解く。
$$

交点が2つの場合は、$${f(x)=g(x)}$$を整理すると基本的に2次方程式になります。つまり、$${f(x),g(x)}$$の3次の係数が共に等しくなければいけません。しかし、ここだけでは公式の導出にはつながらないので次の手順を見てみましょう。

f(x)とg(x)の定積分、そしてその差

ここからは交点のx座標をそれぞれ$${a,b  (a<b)}$$として解説します。まずは定積分とその差を式で表してみましょう。

$$
(面積) = \int_{a}^{b} f(x) dx - \int_{a}^{b}g(x)dx\\
$$

ここで、$${\int_{a}^{b}}$$の部分が同じことに注目すると、次のように変形できますね。

$$
\int_{a}^{b} f(x) dx - \int_{a}^{b}g(x)dx
=\int_{a}^{b}f(x)-g(x)  dx
$$

さて、このとき$${f(x)-g(x)}$$の部分に着目すると、先ほど求めた交点を求める方程式$${f(x)-g(x)=0}$$の左辺と同じであることがわかります。そして、ここで$${F(x)=f(x)-g(x)}$$としておきます。

2次方程式の解の設定

さて、ここで困った点としては、$${a,b}$$を求めるには$${F(x)=0}$$の解は必須ですが、$${F(x)}$$の各項の係数も何もわかっていないことです。まさか4元2次方程式なんてものを解くことはできないので、ここで解を限定してしまいましょう。ここではわかりやすく解を$${x=0,1}$$としておきます。そうすると解の公式から各項の係数を逆算でき、$${F(x)=ax^2-ax  (aは任意の数)}$$であることがわかります。そして、次にこれを定積分するのですが、今回は解が0,1と定まっているので、$${a=0,b=1}$$を代入します。

$$
\int_0^1 ax^2-ax\\
=[\frac{ax^3}{3}-\frac{ax^2}{2}]_0^1\\
=\frac{a}{3}-\frac{a}{2}
$$

ここで、答えとして出したい値を$${n}$$としてみましょう。すると、次のように表すことができます。

$$
n=\frac{a}{3}-\frac{a}{2}\\
6n=2a-3a\\
a=-6n
$$

つまり、$${-6nx^2+6nx=0}$$を解けば解は$${x=0,1}$$になり、さらに左辺を積分するとその値は$${n}$$になるということになります。
つまり、$${F(x)=-6nx^2+6nx}$$ということがわかりました。

公式の導出

さて、$${F(x)}$$が分かったので、ここからはいままでのことを逆算していくだけです。$${F(x)=f(x)-g(x)}$$なので、ここから$${f(x)}$$と$${g(x)}$$の組み合わせを逆算していきます。ただしその前に、$${F(x)=-6nx^2+6x=6n(-x^2+x)}$$と変形しておきます。ここで、$${F(x)=f(x)-g(x)}$$を変形すると、下のようになります。

$$
F(x)=f(x)-g(x)\\
\frac{F(x)}{6n}=\frac{f(x)-g(x)}{6n}\\
-x^2+x=\frac{f(x)-g(x)}{6n}\\
$$

つまり、$${f(x)-g(x)}$$を$${6n×(多項式)}$$の形に変形する(6nをくくり出す)と$${(多項式)=-x^2+x}$$になるということです。よって、6nをくくり出した後の$${f(x),g(x)}$$の間では次のような関係が成り立ちます。

$$
・2次の項の係数の差は-1\\
・1次の項の係数の差は1\\
・3次、0次の項の係数は等しい
$$

これだけだとわかりづらいと思うので、文字で表してみましょう。

$$
f(x)=6n(ax^3+bx+cx+d)\\
g(x)=6n(\alpha x^3+\beta x^2 + \gamma x + \delta)   とおくと、\\
・a=\alpha\\
・b-\beta=-1\\
・c-\gamma=1\\
・d=\delta
$$

逆に言えば、これさえ成り立てば$${f(x),g(x)}$$の式はなんでもいいのです。今回は分かりやすくするために単純にしましたが、上のことさえ成り立っていればいくら複雑にしてもかまいません。
最終的に$${f(x),g(x)}$$の式の例としては次のようになります。

$$
f(x)=6n(x^3-2x^2+2x-1)\\
g(x)=6n(x^3-x^2+x-1)
$$

nは答えにしたい数なので、nを代入して式を展開すれば$${f(x),g(x)}$$がしっかり出てきますね。これを利用して問題を作ってみましょう。
問題の例としては次のようなものになるかと思います。

$$
f_1(x)=12x^3-5x^2-8x+10  , \\
f_2(x)=12x^3-2x^2-11x+10とする。\\
y=f_1(x)とy=f_2(x)のグラフで囲まれた場所の面積を求めよ。
$$

これの答えは解いてみればわかることですが$${\frac{1}{2}}$$です。2次の項,1次の項の差がそれぞれ-3,3になっていることに気づければ6n=3という方程式ができn=$${\frac{1}{2}}$$と簡単に求めることもできます。