ニュートンフラクタル×マンデルブロ集合

108Hassium

2022年11月13日 19:00

どうも、108Hassiumです。

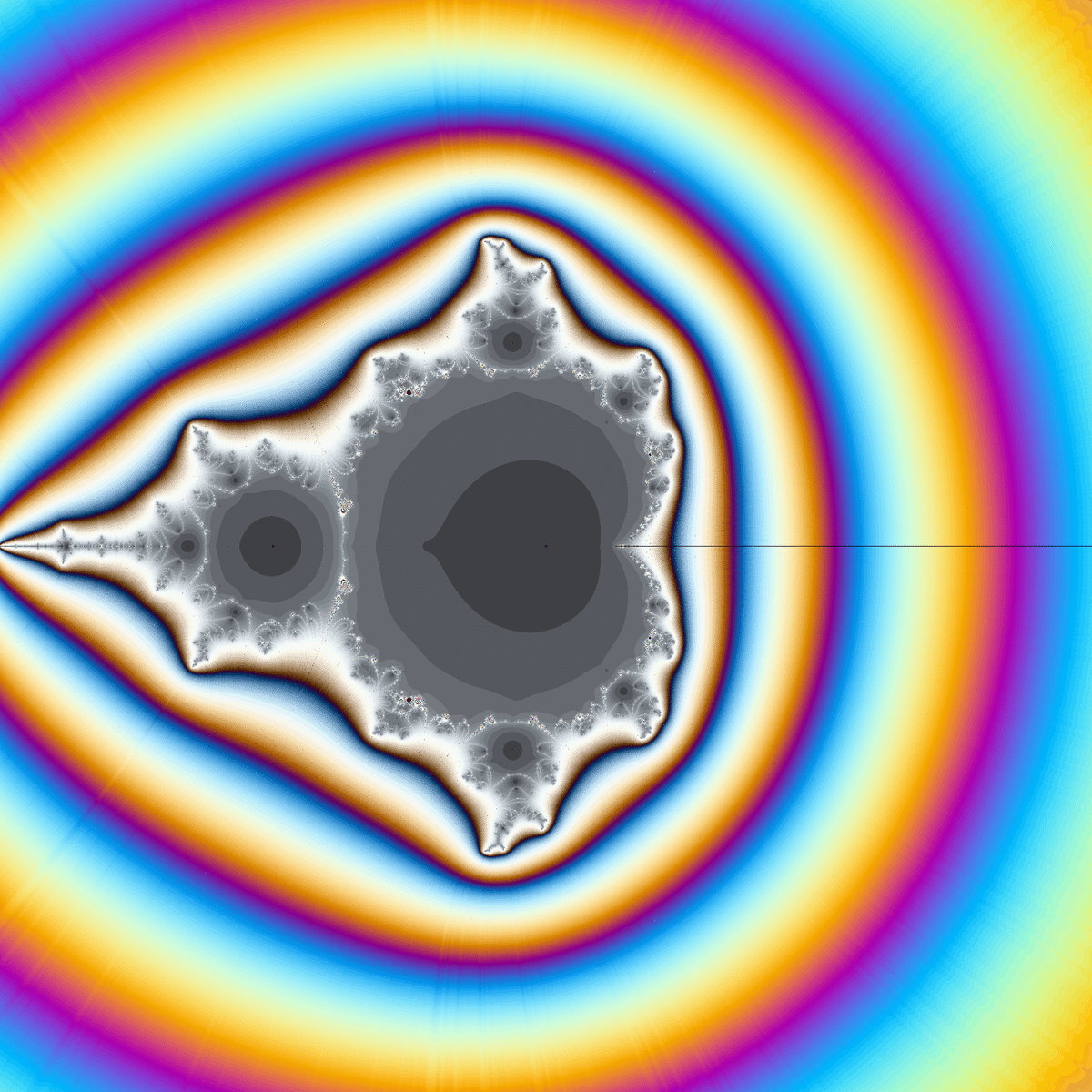
最近、こんなフラクタル図形を発見しました。

$${z^2+c}$$のマンデルブロ集合っぽいシルエットが見えますが、

細部をよく見るとニュートンフラクタルのような複雑な模様が見えます。

この記事では、このフラクタル図形の生成方法や関連するほかの図形を紹介します。

生成方法

あのフラクタル図形は、簡単にいうと「$${f^{10}(z)}$$のニュートンフラクタルのマンデルブロ集合」みたいなものです。

ただし、

$${f(z)=z^2+c}$$
$${f^m(z)=\underbrace{f(f(f(…f(}_mz)…)))}$$

です。

もう少し正確に言うと、複素数$${c}$$に対して以下のような操作をしたものです。

$${z_{n+1}=z_n-\frac{f^{10}(z_n)}{f^{10}(z_n)'},z_{0}=c}$$という数列を計算する。
$${z_n}$$と$${z_{n-1}}$$の差が小さくなったら収束したと見做して、$${n}$$の値を使って$${c}$$を彩色する。

ちなみに、$${\frac{f^m(z)}{f^m(z)'}}$$は以下の漸化式で求められます。

$${a_{m}=\frac{1}{2}a_{m-1}+\frac{(2a_{m-1}-a_{m-2})^2}{8ca_{m-1}},a_0=z,a_1=\frac{z^2+c}{2z}}$$

※この式の導出方法の説明は割愛します。

Processingで実装したコードは以下の通りです。

void setup(){
  size(2000,2000);
  background(0);
  noStroke();
  double x,y,px,py,cx,cy,ax,ay,pax,pay,ppax,ppay;
  boolean o;
  for(int a=0;a<2000;a++){
    for(int b=0;b<2000;b++){
      cx=(double)a/500.0-2.0;
      cy=(double)b/500.0-2.0;
      x=cx;
      y=cy;
      o=true;
      for(int c=0;c<5000000&&o;c++){
        px=x;
        py=y;
        pax=x;
        pay=y;
        ax=divx(x*x-y*y+cx,2.0*x*y+cy,2.0*x,2.0*y);
        ay=divy(x*x-y*y+cx,2.0*x*y+cy,2.0*x,2.0*y);
        for(int d=0;d<10;d++){
          ppax=pax;
          ppay=pay;
          pax=ax;
          pay=ay;
          ax=pax/2.0+divx((2.0*pax-ppax)*(2.0*pax-ppax)-(2.0*pay-ppay)*(2.0*pay-ppay),2.0*(2.0*pax-ppax)*(2.0*pay-ppay),cx*pax-cy*pay,cx*pay+cy*pax)/8.0;
          ay=pay/2.0+divy((2.0*pax-ppax)*(2.0*pax-ppax)-(2.0*pay-ppay)*(2.0*pay-ppay),2.0*(2.0*pax-ppax)*(2.0*pay-ppay),cx*pax-cy*pay,cx*pay+cy*pax)/8.0;
        }
        x=px-ax;
        y=py-ay;
        if((x-px)*(x-px)+(y-py)*(y-py)<1e-10){
          o=false;
          fill(cr(sqrt(c)*17.0),cr(sqrt(c)*18.0)/256.0,cr(sqrt(c)*19.0));
          rect(a,b,1,1);
        }
      }
    }
  }
}

float cr(float c){
  return (c%256)*(256-(c%256))/65;
}

double divx(double a,double b,double x,double y){
  return (a*x+b*y)/(x*x+y*y);
}

double divy(double a,double b,double x,double y){
  return (-a*y+b*x)/(x*x+y*y);
}

応用

$${f(z)}$$の計算回数を減らすと、$${z^2+c}$$のマンデルブロ集合っぽさが薄まる代わりにニュートンフラクタルっぽい線のディティールが目立つようになります。

コードを少し書き換えるだけで、ジュリア集合も描画できます。

ちなみに上の3枚の画像では彩色方法も変えてあって、収束するまでの計算回数$${n}$$のほかに収束先の値の絶対値も色の決定に使っています。(パラメータは画像ごとに個別に微調整してあります)

収束先の絶対値を使った彩色法をマンデルブロ集合の方に適用すると、ジュリア集合では見られなかった繊細で美しいグラデーションが現れます。

しかし、生成された画像をnoteに貼り付けると、何故か上のようにグラデーションがガビガビに崩壊した汚い画像に変換されてしまいます。

☝f(z)=z^2+cのf^11(z)-zのニュートンフラクタルのマンデルブロ集合

$${f^{m}(z)-z}$$の根(の内の$${m}$$個)は、$${z^2+c}$$のジュリア集合の$${m}$$周期サイクルを構成する点になっています。

なので「$${f^{m}(z)-z}$$のニュートンフラクタルを描画したら$${z^2+c}$$のジュリア集合かマンデルブロ集合と関係ある特徴が現れるのでは？」ということを思いつき、$${f^m(z)}$$のやつよりも先にこっちを発見しました。

この画像の描画には、以下の数列を利用しました。

$${a_{n+1}=\frac{b_n^2(a_n-z)^2+(c-z)(a_n-b_n)^2}{2b_n(a_n-z)^2-(a_n-b_n)^2}}$$
$${b_{n+1}=\frac{1}{2}b_n+\frac{c(a_n-b_n)^2}{2b_n(a_n-z)^2}}$$

私の計算が正しければ、$${a_n=\frac{f^n(z)-z}{f^n(z)'-1}}$$が成り立ちます。

余談ですが、上記の数列を計算するコードを書くのがあまりにも面倒臭かったので、今まで使ったことが無かった「クラス」という機能の使い方をわざわざ調べました。(複素数の乗法・除法を愚直に書くと$${a_n}$$の式はめちゃくちゃ長くなり、書き間違いが発生しやすいうえに間違っている場所を探すのが困難になります)