
ニュートンフラクタルと仲間たち
どうも、108Hassiumです。
皆さんはニュートン法というものをご存知でしょうか。
ニュートン法は、例えば$${x^3-2=0}$$のような方程式の解の近似値を求めるアルゴリズムです。
手順は簡単で、解きたい方程式を$${f(x)=0}$$という形にして、初期値を適当に決めて、$${a_{n+1}=a_n-\frac{f(a_n)}{f'(a_n)}}$$という数列を計算するだけです。
例えば$${f(x)=x^3-2}$$とすると、$${a_n}$$は以下のような数列になります。
$${a_{n+1}=a_n-\frac{a_n^3-2}{3a_n^2}}$$
$${a_0=1}$$として計算すると、以下のようになります。
$${a_1=1-\frac{1^3-2}{3×1^2}=\frac{4}{3}=1.3333…}$$
$${a_2=\frac{4}{3}-\frac{(\frac{4}{3})^3-2}{3×(\frac{4}{3})^2}=\frac{91}{72}=1.2638…}$$
$${a_3=\frac{91}{72}-\frac{(\frac{91}{72})^3-2}{3×(\frac{91}{72})^2}=\frac{2253638}{1788696}=1.2599…}$$
実際の解の一つである$${\sqrt[3]{2}}$$も約1.2599なので、少なくとも小数点以下4桁まで一致する近似値が得られていることがわかります。(項数を増やすと精度はもっと上がります)
ちなみに、$${f(x)=0}$$を満たす$${x}$$を「$${f(x)}$$の根」と呼び、ニュートン法のような根の計算法を「求根アルゴリズム」と呼ぶそうです。
ニュートン法の仕組みに関してはwikipediaの説明がこの上なくわかりやすいのでそちらを読んでもらいたいのですが、それはさておきニュートン法には面白い性質があります。
それは、

フラクタル図形の生成に使えるということです。
初期値を複素数にして、どの初期値がどの根に収束したかで複素平面を色分けするとフラクタル図形が出現するようです。
このようなフラクタル図形は「ニュートンフラクタル」と呼ばれ、使用する関数によってさまざまな形に変化します。
また、関数の違い以外にも色々なバリエーションが考えられるので、この記事ではそれらを紹介したいと思います。
普通のニュートンフラクタル
まずは普通のニュートンフラクタルから紹介します。
先ほど載せた画像は$${f(x)=x^3-1}$$としたもので、その前に計算例として使用した$${x^3-2}$$の方は以下のようになります。

どうやら$${x^3-1}$$のものと同じ形っぽいです。
他の関数も試してみます。


$${x^n-1}$$のニュートンフラクタルは、全て$${n}$$回回転対称かつ$${x^3-1}$$と同じような鎖状の模様になるようです。
ただし、

$${n=2}$$のときは全然面白くない形になります。
一般に、2次関数のニュートンフラクタルは面白い形にならないようです。

$${x^n-1}$$のニュートンフラクタルが回転対称性を持つのは複素平面上での根の配置が回転対称になっているからで、根の対称性を崩すとニュートンフラクタルも非対称になります。

さっきの$${x^3-x+1}$$のものと似ていますが、ところどころに真っ黒い領域があります。
この黒領域は、$${x^3-x+1.5}$$の3つの根の内のどれにもたどり着かないような初期値を表しています。

多項式だけでなく、分数関数でもニュートンフラクタルは描画できます。
ちなみに$${x^2-\frac{1}{x}}$$の根は$${x^3-1}$$の根と全く同じ組み合わせなのですが、根が同じでも関数が違えば違うニュートンフラクタルが出来上がるようです。

$${f(x)=\frac{1}{x^2}-1}$$とすると$${x-\frac{f(x)}{f'(x)}=-\frac{1}{2}(x^3-3x)}$$となり、「$${\frac{1}{x^2}-1}$$のニュートンフラクタル」と「$${-\frac{1}{2}(z^3-3z)}$$のジュリア集合」が等しいことがわかります。
一般化ニュートンフラクタル
wikipediaの「Newton fractal」のページ(日本語版は無いようです)には、「Generalization of Newton fractals」(ニュートンフラクタルの一般化)という項目があります。
どうやら、$${z_{n+1}=z_n-a\frac{f(z_n)}{f'(z_n)}}$$という式によりニュートンフラクタルの亜種みたいなものをつくれるようです。


だいぶ印象が違いますが、3回回転対称であることは変わらないようです。

元々繋がっていた部分が離れ、壊れかけみたいな感じになりました。(黒領域も消えています)

各領域の明るさは収束の速度によって変化し、収束が遅いと同心円状の縞模様が現れます。
普通のニュートン法は収束がかなり速いので縞模様にはなりませんが、一般化ニュートンフラクタルは$${a}$$が1から離れるとだんだん収束が遅くなるようです。

一般化ニュートンフラクタルなら、2次関数でも面白い形が生成できるようです。
Nova fractal
一般化ニュートンフラクタルのさらなる一般化として、Nova fractalというものもwikipediaに載っています。
Nova fractalの漸化式は以下の通りです。
$${z_{n+1}=z_n-a\frac{f(z_n)}{f'(z_n)}+c}$$
一般化ニュートンフラクタルの式に対して、新たな変数$${c}$$が追加されています。

一般化ニュートンフラクタルには「$${a}$$が1から離れるとだんだん収束が遅くなり、ある程度離れると$${f(x)}$$の根には収束しなくなる」という性質がありました。
しかし、Nova fractalの場合は$${c}$$を0から少しでもずらすと$${f(x)}$$の根に収束しなくなります。
なので収束先ごとに色分けする意味が薄いと思ったので、今までのものとは別の彩色方法を使っています。


wikipediaでは、$${c}$$を動かす「Nova fractalのマンデルブロ集合」についても言及しています。

wikipediaには「$${f(x)=x^3-1}$$なら臨界点は1になる」的な感じの記述があるのですが、実際は臨界点が1になるのは$${a=1}$$のときだけで、$${a}$$を動かすと臨界点も変化します。(臨界点は4次方程式の解になります)


Nova fractalはもはやニュートン法とはほとんど関係ないただのジュリア集合で、ジュリア/マンデルブロ集合の生成式としては臨界点が簡単に求まらないので不便です。
Nova fractalと似たようなものが生成出来てなおかつもっと使い勝手のいい式はいくらでもありそうなので、個人的にはNova fractalはあまり面白くない気がします。(例えば、$${c(z+\frac{1}{2z^2})+d}$$という式を使えば$${x^3-1}$$のNova fractalとよく似たフラクタル図形を生成出来ます)
簡易ニュートン法
さて、ここまでの内容はただwikipediaに書いてあることをなぞっただけです。
ニュートン法のページには関連するほかの求根アルゴリズムがいくつか載っていますが、それらを使ったフラクタル図形については何も言及がありません。
というわけで、ニュートン法以外の求根アルゴリズムでもニュートンフラクタルのようなフラクタル図形が生成されるのか実験してみます。
まず初めに、簡易ニュートン法を試してみます。
簡易ニュートン法はニュートン法における導関数の計算を簡易化したもので、以下の漸化式を使います。
$${z_{n+1}=z_n+\frac{f(z_n)}{f'(z_0)}}$$

中央から6方向にのびているカラフルな領域は、$${z_n}$$が発散する領域です。
普通のニュートンフラクタルはジュリア集合の一種でしたが、簡易ニュートンフラクタルはマンデルブロ集合の一種です。
例えば$${f(x)=x^3-1}$$のとき、$${z_0=c}$$とすると$${f(x)}$$の簡易ニュートンフラクタルは「$${c}$$を初期値とする$${z-\frac{z^3-1}{3c^2}}$$のマンデルブロ集合」と見做せます。(ちなみに$${c}$$は$${z-\frac{z^3-1}{3c^2}}$$の臨界点の一つです)

拡大してみると、いかにもマンデルブロ集合っぽい形になっていることがわかります。


q-ニュートン法
q-ニュートン法は、ニュートン法に対して新たな変数$${q}$$を追加したもので、定義は以下の通りです。
$${z_{n+1}=z_n-\frac{(q-1)f(x)}{f(qz_n)-f(z_n)}}$$
※wikipediaに載っている式は微妙に違うのですが、参考文献として挙げられている論文をパッと見た感じだとこっちが正しそうです。
この手法が何のために開発され、どの様な性質を持っているのか等は全く分かりませんが、とりあえず$${q}$$に適当な値を入れてq-ニュートンフラクタルを描画してみました。

何だか見覚えのある形になりました。
$${a=1.7}$$の$${x^3-1}$$の一般化ニュートンフラクタルとそっくりです。

実は、$${x^3-1}$$のq-ニュートンフラクタルの式を整理すると$${z_{n+1}=z_n-\frac{z_n^3-1}{(q^2+q+1)z_n^2}}$$になり、$${a=\frac{3}{q^2+q+1}}$$とすると一般化ニュートンフラクタルの式と一致します。

※臨界点は綺麗に求まりませんでした。
$${x^3-1}$$の根に収束する3色の領域に加え、他の値に収束する黒の領域、カオス的になるノイズ状の領域、無限大に発散する虹色の領域という計6種類の領域が混ざり合っています。

$${f(x)=x^3-x+1.5}$$の場合は$${z_{n+1}=z_n-\frac{z_n^3-z_n+1.5}{(q^2+q+1)z_n-1}}$$になり、一般化ニュートンフラクタルとは違う式になります。




$${x^3-1}$$と違い、$${x^3-x+1.5}$$のq-ニュートンフラクタルは根に到達する領域が黒領域や発散領域と混在するのが特徴的です。

右下の緑の領域をよく観察すると、黒い領域がめり込んでいたり、縁の部分が発散領域に切り取られたような形になっており、それらの領域は黒領域・発散領域と混在する値に対応しています。(q=-1.5+0.2iは右側の方の値で、これも青と黒の領域が重なった位置にあります)
改良ニュートン法
wikipediaのニュートン法のページの「改良」の項目の一番最初に載っているもの(名前は不明)を試してみました。

収束しない領域があるようです。
wikipedia曰く通常のニュートン法より収束が速いのが長所らしいのですが、完全な上位互換というわけでもないようです。
ちなみに漸化式は以下のようになりました。
$${z_{n+1}=\frac{10}{19}z_n+\frac{234z_n^4+9z_n}{361z_n^6+133z_n^3+19}}$$
次数が高く係数もでかいです。
式が複雑になるなら2次関数でも面白い形になるのでは、と思って$${x^2-1}$$を試してみました。

つまんねぇ~。
割線法
ニュートン法のページには載っていませんが、こんなものを見つけました。
割線法では導関数の計算が要らない代わりに、新しい項を計算するのに二つ前までの項を利用します。
普通のジュリア集合やマンデルブロ集合とは漸化式の種類が違うので、違った感じのフラクタル図形になりそうです。

発散領域が所々に散らばっていて、かなり華やかな見た目になりました。

今までのものとは違って初期値に相当するパラメータが2つあり、その組み合わせによって違った見た目のフラクタル図形が生成されるようです。




簡易割線法
こんな求根アルゴリズムを思いつきました。
$${z_n=z_n-\frac{cf(z_n)}{f(z_n+c)-f(z_n)}}$$
これは割線法の$${z_{n-1}}$$を$${z_n+c}$$に置き換えたものです。

非対称なうえに赤一色になりました。

常に1個の根にしか収束しないのかと思いきや、そうでもないようです。
どうやら$${c}$$の値が特定の根に近いと、その根に収束しやすくなるようです。

3色が混ざることもあるようです。

導関数の定義より、$${\displaystyle{\lim_{c→0}}\frac{f(x+c)-f(x)}{c}}$$は明らかに$${f'(x)}$$と等しいので、簡易セカントフラクタルの$${c→0}$$の極限はニュートンフラクタルと一致します。($${f(x)}$$が多項式なら、$${c}$$に0を直接代入できるような式変形ができるようです)

※臨界点は綺麗に求まりませんでした。


2次関数からでもフラクタル図形が生成できるようですが、$${z^2+c}$$のジュリア集合と似たような形ばかりであまり面白くは無いようです。
第2簡易割線法
$${z_n=z_n-\frac{f(z_n)(z_n-c)}{f(z_n)-f(c)}}$$
割線法の$${z_{n-1}}$$を定数$${c}$$に置き換えてみました。
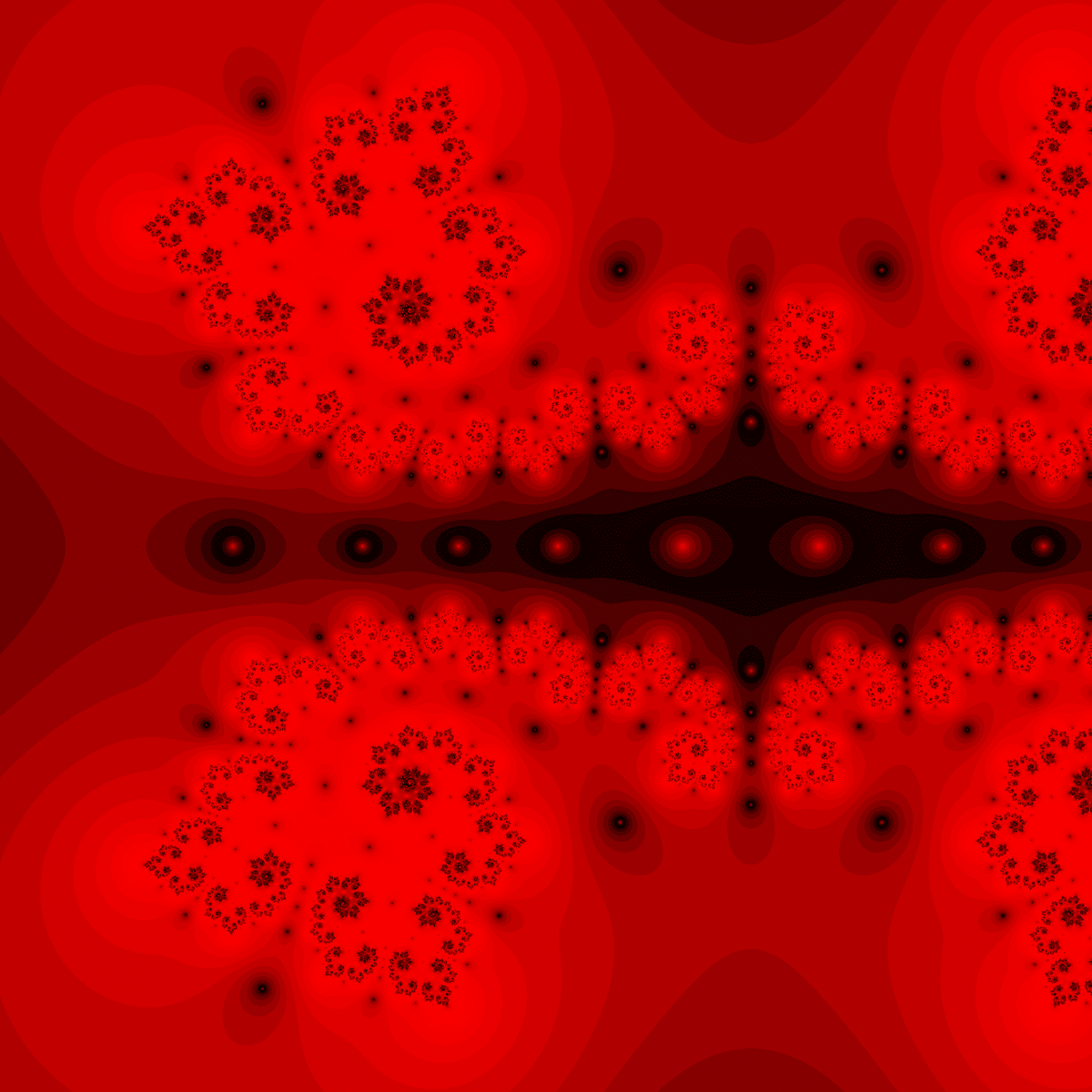


全体の形は3回回転対称にはならないものの、点対称(原点中心ではない)になるようです。

おまけ:多重ニュートンフラクタル
最後に、記事の主題とは離れますが面白いと思った話題を紹介します。
「$${f(x)}$$のニュートンフラクタル」は「$${z-\frac{f(z)}{f'(z)}}$$のジュリア集合」でもあるわけですが、それなら「$${x-\frac{f(x)}{f'(x)}}$$のニュートンフラクタル」というものを考えることもできるはずです。
また、「$${x-\frac{f(x)}{f'(x)}}$$のニュートンフラクタル」=「$${g(z)}$$のジュリア集合」となるような関数$${g(z)}$$に対するニュートンフラクタルだって存在するはずです。
これを一般化して、以下のような関数列を定義します。
$${f_{n+1}(x)=x-\frac{f_n(x)}{f_n'(x)}}$$
適当な関数を$${f_0(x)}$$に選んで$${f_n(x)}$$のニュートンフラクタルを順番に描画していったらどうなるでしょうか?
というわけで、まずは$${f_0(x)=x^3-1}$$を選びました。

今まで何度も見てきた、$${x^3-1}$$のニュートンフラクタルです。

細部の形は$${f_0(x)}$$のものと似ていますが、違った形のニュートンフラクタルになりました。
これからさらに面白い形になっていきそうですね。

あれ?

え?

は?

つまんねぇ~。
どうやら最初の2個が特殊だったようで、その後は2種類の形が交互に並ぶだけになるようです。
ちなみに$${f_n(x)}$$は以下のような式になりました。
$${f_0(x)=x^3-1}$$
$${f_1(x)=\frac{2}{3}x+\frac{1}{3x^2}}$$
$${f_2(x)=-\frac{3x}{2x^3-2}}$$
$${f_3(x)=\frac{3}{2}x-\frac{3x}{4x^3+2}}$$
$${f_4(x)=\frac{3x}{2x^3+4}}$$
$${f_5(x)=\frac{3}{2}x+\frac{3x}{2x^3-2}}$$
$${f_6(x)=-\frac{3x}{x^3-4}}$$
$${f_7(x)=\frac{3}{2}x-\frac{3x}{x^3+2}}$$
$${f_8(x)=\frac{6x}{x^3+8}}$$
規則性はよくわかりませんが、似たような式ばかりですね。
フラクタル図形の話題としては面白く無いですが、これはこれで数学的におもしろいかもしれませんね。
次は$${x^4-1}$$です。




またかよ。
どうやらある程度簡単な形(基準は不明)の関数だと、途中で根の個数が減って面白さが枯渇するようです。
$${f_0(x)=x^3-x+1}$$の場合は、そのような傾向はみられませんでした。



$${f_0(x)=x^3-x+1}$$
$${f_1(x)=\frac{2}{3}x+\frac{2x-3}{9x^2-3}}$$
$${f_2(x)=-\frac{4x^3-9x^2+1}{6x^4-6x^2+6x}}$$
$${f_3(x)=2x+\frac{9}{4}+\frac{130x^5+36x^4-36x^3-77x^2+18x-9}{16x^6-72x^5+16x^4-16x^3+36x^2-8x+4}}$$
この先はめちゃくちゃ複雑な式になりそうなので計算を諦めました。
$${f_0(x)=x^2+x-1}$$は、かなり意外性のある結果になりました。

$${f_1(x)=\frac{1}{2}x-\frac{1}{4}-\frac{5}{8x+4}}$$

$${f_2(x)=\frac{1}{2}-\frac{5x}{2x^2+2x-2}}$$

$${f_3(x)=-\frac{1}{5}x^2+\frac{8}{5}x+\frac{7}{5}-\frac{6x+8}{5x^2+5}}$$

$${f_4(x)=\frac{1}{2}x+2+\frac{23x^4-9x^3+42x^2+29x+3}{2x^5-8x^4+4x^3-22x^2-14x-2}}$$
最初の2個は面白くない形だったのに、急に面白くなりました。
追記:メーリーの手順
記事の投稿後、wikipediaを眺めてたら面白いものを新たにいくつか見つけたので追記します。
まず、ニュートン法の英語版のページで「Maehly's procedure」という項目を見つけました。
$${f(x)}$$の根$${x_1,x_2,x_3…}$$がすでに見つかっている場合、$${f(x)}$$の代わりに$${\frac{f(x)}{(x-x_1)(x-x_2)(x-x_3)…}}$$のニュートン法の計算をすることで未発見の根を見つけられるだろう、とのことです。
これを基にして、以下のような操作を考えました。
$${f(x)}$$ニュートン法の計算をして、根$${r}$$を1個求める
$${\frac{f(x)}{x-r}}$$のニュートン法の計算をして、収束先に応じて初期値を彩色する

領域の境界線は普通のニュートンフラクタルとほぼ同じですが、色分けのされ方が変わりました。
新たに出現した3本の直線は、$${\frac{x^3-1}{x-1}}$$、$${\frac{x^3-1}{x-\frac{-1+\sqrt{-3}}{2}}}$$、$${\frac{x^3-1}{x-\frac{-1-\sqrt{-3}}{2}}}$$のニュートンフラクタルの境界線で、3つとも2次関数なので直線になっています。

$${f(x)}$$が4次だと$${\frac{f(x)}{x-r}}$$は3次になるので、5種類のフラクタル図形が混ざり合った複雑な模様が出来上がります。
ただし、異なる種類のフラクタル図形が重なっただけのような見た目になるので美しさはイマイチです。
ハレー法
ニュートン法の日本語版のページには「反復法」というページへのリンクがあり、反復法のページには「ハレー法」という求根アルゴリズムが載っています。
どうやら改良ニュートン法と同じく、収束の速さが売りの手法らしいです。

なんか見覚えが・・・と思ったら、実は最初の方で紹介した$${x^2-\frac{1}{x}}$$のニュートンフラクタルと全く同じです。
元々「分数関数でもニュートンフラクタルが作れる」「根が同じでも関数が違えば違うニュートンフラクタルになる」ということの説明をするだけの為に載せていたのですが、まさかこんな裏の顔があるとは思いませんでした。


ハウスホルダー法
ニュートン法とハレー法の一般化として、ハウスホルダー法というものがあるようです。
$${g(x)=\frac{1}{f(x)}}$$として、$${a_{n+1}=a_n+d\frac{g^{(d-1)}(a_n)}{g^{(d)}(a_n)}}$$($${g^{(d)}(x)}$$は$${g(x)}$$の$${d}$$階導関数という数列を計算するという手法で、$${d=1}$$がニュートン法、$${d=2}$$がハレー法だそうです。









地味ですね。
